Элементы теории корреляции

 

Теоретические сведения и примеры решения задач

 

Выборочный коэффициент корреляции:

,

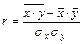где 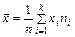, 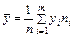- выборочные средние Х и Y;

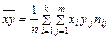- среднее значение величины ХY;

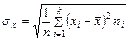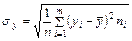, - выборочные
средние квадратические отклонения Х и Y.

Выборочное уравнение регрессии Y на X:

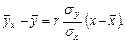
Выборочное уравнение регрессии X на Y:

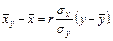
Для оценки достоверности коэффициента корреляции проверяется гипотеза Н₀ об отсутствии линейной корреляционной связи между переменными в генеральной совокупности, т.е. Н₀: 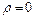, по следующей схеме:

а) вычисляется статистика 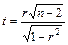отклонения выборочного коэффициента корреляции от генерального коэффициента корреляции 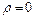, где n – число наблюдений;

б) по таблице критических точек (двусторонней критической области) распределения Стьюдента (таблица А3 Приложения А) на уровне значимости 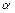и при числе степеней свободы 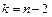находится значение ;

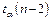в) если не выполняется неравенство 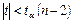, гипотеза Н₀
отвергается, т.е. выборочный коэффициент корреляции существенно

отличается от нуля, что свидетельствует о достоверности коэффициента корреляции.

 

Задача. Для исследования зависимости объема производства (Y) от основных фондов (Х) получены статистические данные по 70 предприятиям за год.

 

Y	Х тыс. руб

 

Предполагая, что между Х и Y существует линейная корреляционная зависимость, необходимо: а) определить коэффициент корреляции и сделать вывод о тесноте и направлении связи; б) оценить достоверность коэффициента корреляции 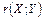на 5 %-ном уровне значимости; в) найти уравнения прямых регрессии.

Решение. Вычислим средние выборочные 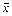и :

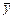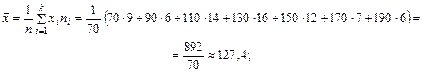
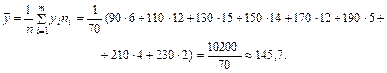
Найдем среднее значение величины ХY:

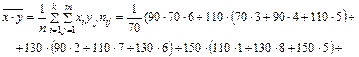
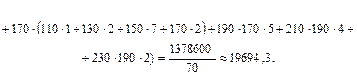
Вычислим дисперсии, а затем средние квадратические отклонения Х и Y:

.

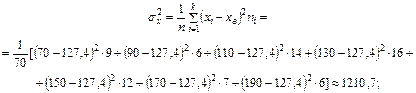
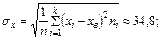
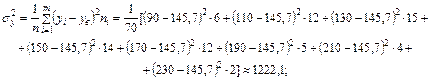
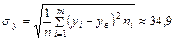Вычислим выборочный коэффициент корреляции:

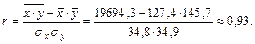
Полученное значение выборочного коэффициента корреляции показывает, что между переменными Х и Y существует достаточно тесная связь, близкая к линейной. Поскольку 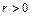, то эта связь возрастающая, т.е. по мере увеличения основных фондов увеличивается объем производства.

Оценим достоверность коэффициента корреляции 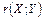на 5%-ном уровне значимости. Для этого найдем статистику критерия по формуле :

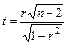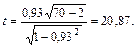
Для уровня значимости 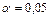и числа степеней свободы 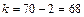по таблице А3 Приложения А находим критическое значение статистики 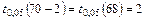. Поскольку 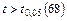, то коэффициент корреляции достоверен на 5%-ном уровне значимости.

Выборочное уравнение прямой регрессии Y на Х имеет вид:

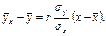
Подставляя все найденные значения в последнее уравнение, получаем:

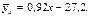
Аналогично найдем выборочное уравнение прямой регрессии Х на Y:

 

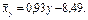
Варианты задачи № 9

 

Для исследования зависимости величины Y от величины Х получено распределение, статистические данные сведены в таблицу. Предполагая, что между Х и Y существует линейная корреляционная зависимость, необходимо:

а) определить коэффициент корреляции и сделать вывод о тесноте и направлении связи;

б) оценить достоверность коэффициента корреляции на 5%-ном уровне значимости;

в) найти уравнения прямых регрессии и построить их на одном чертеже,

г) используя соответствующее уравнение регрессии, получить среднюю величину Y, если Х = х ₀, или среднюю величину Х, если
Y =y ₀.

 

1. Х – расходы фирмы на рекламу (ден. ед.), Y – еженедельные продажи фирмы (ден. ед), 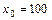ден. ед.

Y	X

2. Распределение 100 деревьев, Х – диаметр дерева (м), Y – высота дерева (м), м.

 

Y	X
0-0,8	0,8-1,6	1,6-2,4	2,4-3,2	3,2-4	4-4,8
0,16-0,22
0,22-0,28
0,28-0,34
0,34-0,4
0,4 -0,46
0,46-0,52
0,52-0,58
0,58-0,64

 

3. Распределение 100 шоферов-любителей, Х – возраст шофера (лет), Y – число водителей, использующих ремень безопасности, 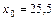лет.

 

Y	X
0-10	10-20	20-30	30-40	40-45
15-18
18-21
21-24
24-27
27-30

 

4. Распределение 116 телевизоров, Х – чувствительность видеоканала (мкВ), Y – чувствительность звукового канала 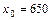(мкВ), мкВ.

 

Y	X
0-100	100-200	200-300	300-400	400-500	500-600
0-100
100-200
200-300
300-400
400-500
500-600

 

5. Распределение 100 предприятий, Х – производительность
труда (тыс. руб./чел.), Y – себестоимость продукции (тыс. руб./изд.), 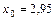тыс. руб./чел.

 

Y	X
2,7-3,2	3,2-3,7	3,7-4,2	4,2-4,7	4,7-5,2	5,2-5,7
2,0-2,6
2,6-3,2
3,2-3,8
3,8-4,4
4,4-5,0
5,0-5,6
5,6-6,2

 

6. Распределение 100 предприятий, Х – затраты на электроэнергию (тыс. руб./ед. продукции), Y – прибыль от реализации изделия (тыс. руб.), 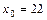тыс. руб.

 

Y	X
6,0-6,8	6,8-7,6	7,6-8,4	8,4-9,2	9,2-10,0
16-20
20-24
24-28
28-32
32-36
36-40

 

7. Распределение 50 школьников, Х – мышечная сила правой кисти рук (кг), Y – мышечная сила левой кисти рук 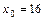(кг), кг.

Y	X
11,8-12,2	12,2-12,6	12,6-13	13-13,4	13,4-13,8	13,8-14,2
13.8-14,2
14,2-14,6
14,6-15
15-15,4
15,4-15,8
15,8-16,2
16,2-16,6

 

8. Распределение 100 фабрик, Х – число изделий, изготавливаемых рабочим за смену (шт.), Y – размер заработной платы (тыс. руб.), 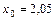тыс. руб.

 

Y	X
55-115	115-175	175-235	235-295	295-355	355-415
0-2
2-4
4-6
6-8
8-10

 

9. Распределение 50 однотипных предприятий, Х – себестои-мость выпуска единицы продукции (тыс. руб.), Y – основные фонды (млн руб.), 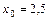тыс. руб.

 

Y	X
1,25	1,5	1,75	2,0	2,25
80-130
130-280
180-230
230-280
280-330

 

10. Распределение 200 драгоценных изделий, Х – стоимость изделия (тыс. руб.), Y – количество примесей (%), 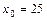тыс. руб.

 

Y	X
3-9	9-15	15-21	21-27	27-33	Более 33
20-30
30-40
40-50
50-60
60-70
70-80
80-90

 

11. Распределение 140 предприятий, Х – производственные затраты (млн руб.), Y – степень компьютеризации производства (%), 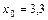млн руб.

 

Y	X
2,0-2,5	2,5-3,0	3,0-3,5	3,5-4,0	4,0-4,5	4,5-5,0
10-20
20-30
30-40
40-50
50-60
60-70

 

12. Распределение 100 модернизированных приборов, Х – степень модернизации (%), Y – количество сбоев за месяц работы (шт), %.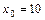

 

Y	X
2,5-4	4-5,5	5,5-7	7-8,5	8,5-10	10,5-11	11,5-13
2-3
3-4
4-5
5-6
6-7
7-8
8-9

 

13. Распределение 70 предприятий, Х – объем выпуска про-дукции (тыс. шт.), Y – себестоимость единицы изделия (тыс. руб.), 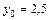тыс. руб.

 

Y	X
2,2-2,4	2,4-2,6	2,6-2,8	2,8-3,0	3,0-3,2	3,2-3,4
0,5-1,5
1,5-2,5
2,5-3,5
3,5-4,5
4,5-5,5
5,5-6,5

14. Распределение 100 работников компании, Х – показатели работы (баллы), Y – результаты тестирования (баллы), 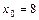баллов.

 

Y	X
5-6	6-7	7-8	8-9	9-10
9-11
11-13
13-15
15-17
17-19
19-21

 

15. Распределение 50 компаний, занимающихся грузовыми перевозками, Х – среднемесячный доход (млн руб.), Y – количество машин (ед.), 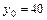машин.

 

Y	X
70-75	75-80	80-85	85-90	90-95
20-30
30-40
40-50
50-60
60-70

 

16. Распределение 60 образцов сырья по процентному содержанию минерала Х (%) и процентному содержанию минерала Y (%), %.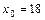

 

Y	X
10-12	12-14	14-16	16-18	18-20
20-30
30-40
40-50
50-60
60-70

 

17. Распределение50 компаний, Х – ежемесячные расходы компании на рекламу (тыс. руб.), Y – объем выручки от продаж (млн руб.), 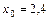тыс. руб.

Y	X
2,0-2,2	2,2-2,4	2,4-2,6	2,6-2,8	2,8-3,0
28-32
32-36
36-40
40-44
44-48
48-52

 

18. Распределение120 служащих, Х – потери рабочего времени (%), Y – сумма начислений на заработную плату, вызванная ростом производительности труда 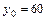(у.е.), у.е.

 

Y	X
3-5	5-7	7-9	9-11	11-13
20-30
30-40
40-50
50-60
60-70
70-80

 

19. Распределение 50 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 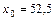тыс. руб.

 

Y	X
12,5	17,5	22,5	27,5	32,5	37,5	42,5	47,5
200-210
210-220
220-230
230-240
240-250
250-260
260-270
270-280
280-290

 

20. Распределение 55 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 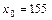тыс. руб.

Y	X
30-50	50-70	70-90	90-110	110-130	130-150
50-70
70-90
90-110
110-130
130-150
150-170

 

21. Распределение 100 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 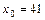тыс. руб.

 

Y	X
13,5	18,5	23,5	28,5	33,5	38,5	43,5	48,5
100-110
110-120
120-130
130-140
140-150
150-160
160-170
170-180
180-190

 

22. Распределение 100 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 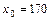тыс. руб.

 

Y	X
40-60	60-80	80-100	100-120	120- 140	140 - 160
60-80
80-100
100-120
120-140
140-160
160-180

 

23. Распределение 60 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 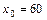тыс. руб.

 

Y	X
12,6	17,6	22,6	27,6	32,6	37,6	42,6	47,6	52,6
202-212
212-222
222-232
232-242
242-252
252-262
262-272
272-282
282-292
292-302

 

24. Распределение 54 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 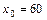тыс. руб.

 

Y	X
14,5	19,5	24,5	29,5	34,5	39,5	44,5	49,5	54,5
300-310
310-320
320-330
330-340
340-350
350-360
360-370
370-380
380-390
390-400

 

25. Распределение 65 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 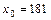тыс. руб.

 

Y	X
32-52	52-72	72-92	92-112	112-132	132-152	152-172
48-68
68-88
88-108
108-128
128-148
148-168
168-188
188-208

 

26. Распределение 60 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 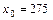тыс. руб.

 

Y	X
130-150	150-170	170-190	190-210	210-230	230-250	250-270
150-170
170-190
190-210
210-230
230-250
250-270
270-290
290-310

 

27. Распределение 55 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 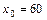тыс. руб.

 

Y	X
12,5	17,5	22,5	27,5	32,5	37,5	42,5	47,5	52,5
250-260
260-270
270-280
280-290
290-300
300-310
310-320
320-330
330-340
340-350

 

28. Распределение 65 предприятий, Х – основные фонды
(тыс. руб.), Y – объем производства (ед.), 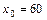тыс. руб.

 

Y	X
60-80	80-100	100-120	120-140	140-160	160-180	180-200
100-120
120-140
140-160
160-180
180-200
200-220
220-240
240-260

29. Распределение80 служащих, Х – потери рабочего времени (%), Y – сумма начислений на заработную плату, вызванная ростом производительности труда 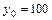(у.е.), у.е.

 

Y	X
2-4	4-6	6-8	8-10	10-12	12-14
30-40
40-50
50-60
60-70
70-80

 

30. Распределение 100 фабрик, Х – число изделий, изготавливаемых рабочим за смену (шт), Y – размер заработной платы (тыс. руб.), 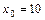тыс. руб.

 

Y	X
54-114	114-174	174-234	234-294	294-354	354-414
1-3
3-5
5-7
7-9
9-11

 

9.3 Теоретические вопросы к защите расчетного задания № 9

 

1. Как определяется зависимость между признаками: а) функциональная; б) вероятностная; в) корреляционная?

2. В чем заключается задача: а) корреляционного анализа; б) регрессионного анализа?

3. Что называется диаграммой рассеяния или корреляционным полем?

4. В чем состоит разница в понятиях «теоретический коэффициент корреляции» и «выборочный коэффициент корреляции»?

5. Как определяется выборочный коэффициент корреляции?

6. Сформулируйте свойства выборочного коэффициента корреляции.

7. Какой вид имеет уравнение регрессии переменной Y на Х в случае линейной регрессионной модели?

8. Как оценивается теоретическая прямая регрессии переменной Y на Х?

9. Как определяется точечный прогноз среднего значения зависимой переменной Y при заданном значении независимой переменной Х?

10. Что можно сказать о характере зависимости между случайными величинами Х и Y при: а) r = 0; б) r = 1; в) r = -1?

 

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: