 |
=мумнож(мобр(мумнож(а2:в3; а2:в3));d2:d3)
|
|
|
|
=МУМНОЖ(МОБР(МУМНОЖ(А2: В3; А2: В3)); D2: D3)
5. Завершите ввод формулы нажатием комбинации клавиш < Ctrl> +< Shift> +< Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива:
{=МУМНОЖ(МОБР(МУМНОЖ(А2: В3; А2: В3)); D2: D3)}
В диапазоне ячеек F2: F3 будет найдено решение системы уравнений

Нахождение значения квадратичной формы
Рассмотрим пример вычисления квадратичной формы  , при этом
, при этом

Для нахождения этой квадратичной формы:
1. Введем элементы матрицы A в диапазоне ячеек А2: В3 и вектора X в диапазоне ячеек D2: D3.
2. Выберем ячейку F2 для вычисления значения формы.
3. Введем формулу:
=МУМНОЖ(МУМНОЖ(ТРАНСП(D2: D3); A2: B3); D2: D3)
4. Завершим ввод формулы нажатием комбинации клавиш < Ctrl> +< Shift> +< Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива (см. рис. 6. 6):
{=МУМНОЖ(МУМНОЖ(ТРАНСП(D2: D3); A2: B3); D2: D3)}

Рис. 6. 6. Нахождение значения квадратичной формы
В ячейке F2 будет получено искомое значение формы 196.
Примеры использования матричных операций в экономических задачах
Пример 1. Данные о доходах (тыс. ден. ед. ) холдинговой компании по трем регионам трех компаний за 2000 и 2002 гг. представлены в матрицах А и В:

Здесь элемент aijматрицы Аозначает доход i-й компании в j-м регионе за 2000 г. Аналогично – для матрицы В, но за 2002 г. Вычислите матрицу С приростов доходов за период с 2000 по 2002 г. и проанализируйте ее. Рассчитайте матрицу Сср, характеризующую средние размеры приростов доходов компаний холдинга за год.
Решение.
1) Матрица С приростов доходов за рассматриваемый период равна:
|
|
|
С = В – А.
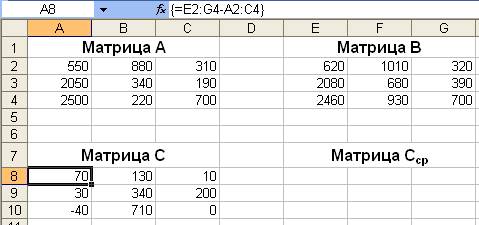
Элементы матрицы Свыражают изменение доходов с 2000 по 2002 г. Так, третья компания по первому региону потерпела убытки в размере 40 тыс. ден. ед. (c31 = - 40), эта же компания (третья) по третьему региону в этот же период не принесла доходов (с33 = 0).
2) Матрица Сср, характеризующая средние размеры приростов доходов компаний холдинга за год, равна матрице С, деленной на n— количество лет в рассматриваемом периоде. В период с 2000 по 2002 г. входит 2 года (т. е. 2000 и 2001гг. ), значит, n= 2, тогда: Сср = C/2

Пример 2. Предприятие производит продукцию трех видов. При этом используется сырье трех типов. Нормы затрат сырья на единицу продукции каждого вида, себестоимость каждого вида сырья и стоимость его доставки приведены в таблице.
|
Показатель |
Норма затрат сырья на единицу продукции, у. е. | ||
| I тип | II тип | III тип | |
| Вид продукции | |||
| Себестоимость единицы сырья, ден. ед. | |||
| Стоимость доставки единицы сырья, ден. ед. | |||
Каковы общие затраты предприятия на производство 100 у. е. продукции первого вида, 75 у. е. второго вида и 50 у. е. третьего вида?
Решение.
Нормы расходов сырья на единицу продукции запишем в виде матрицы А:
 ,
,
у которой элементы аij выражают количество сырья j-го типа на изготовление единицы изделия i-го вида. Пусть матрица С характеризует себестоимость единицы сырья и стоимость доставки единицы сырья:

Объем производства продукции задается матрицей-столбцом

Чтобы определить общие затраты S на производство продукции данного объема Q, надо знать затраты Рна сырье для производства единицы продукции каждого вида и его доставку. Для этого умножим матрицу расходов Ана матрицу Ст. Получим:
P = A · Ст

Тогда суммарные затраты составят S = QT · P:

Пример 3. Фабрика специализируется на выпуске изделий трех типов. При этом используется сырье трех видов: S1, S2, S3. Нормы расхода каждого из них на единицу продукции каждого типа и объем расхода сырья на 1 день заданы таблицей:
|
|
|
|
Вид сырья |
Нормы расхода на единицу продукции | Объем сырья | ||
| 1 тип | II тип | III тип | на 1 день | |
| S1 | ||||
| S2 | ||||
| S3 | ||||
Найдите ежедневный объем выпуска продукции каждого типа, учитывая, что сырье должно быть использовано полностью.
|
|
|


