 |
=суммпр0изв(вз:f6;в8:f11). 7. 4. Задача о назначении. Стоимость выполнения работ. Рабочие. Виды работ. =суммпроизв(а2:d5; f2:i5)
|
|
|
|
=СУММПР0ИЗВ(ВЗ: F6; В8: F11)
6. В ячейки диапазонов G8: G11 введите формулы, вычисляющие объемы производства на фабриках, в ячейки диапазона B12: F12 объемы доставляемой продукции в пункты распределения. А именно:
| Ячейка | Формула | Ячейка | Формула |
| G8 | =CУMM(B8: F8) | B12 | =СУММ(В8: В11) |
| G9 | =CУMM(B9: F9) | C12 | =СУММ(С8: С11) |
| G10 | =CУMM(B10: F10) | D12 | =CУMM(D8: D11) |
| G11 | =CУMM(B11: F11) | E12 | =СУММ(Е8: Е11) |
| F12 | =CУMM(F8: F11) | ||
7. Выберите команду Сервис – Поиск решения и заполните диалоговое окно Поиск решения, как показано на рис. 7. 8.
8. Нажмите кнопку Выполнить. Средство Поиск решения найдет оптимальный план поставок продукции и соответствующие ему транспортные расходы (рис. 7. 9).

Рис. 7. 8. Заполненное диалоговое окно Поиск решения для транспортной задачи

Рис. 7. 9. Оптимальное решение транспортной задачи
7. 4. Задача о назначении
В данном разделе продемонстрируем, как средство Поиск решения позволяет решать задачу о назначении.
В нашем конкретном случае задача о назначении формулируется следующим образом. Имеются четыре рабочих и четыре вида работ. Стоимости Сijвыполнения i-ым рабочим j-ой работы приведены в таблице, где под строкой понимается рабочий, а под столбцом – работа:
Стоимость выполнения работ
|
Рабочие | ||||
|
Виды работ
| ||||
Необходимо составить план выполнения работ таким образом, чтобы все работы оказались выполненными, каждый рабочий был загружен только на одной работе, а суммарная стоимость выполнения всех работ была минимальной.
Замечание . Данная задача является сбалансированной, т. е. число работ совпадает с числом рабочих. Если задача несбалансированна, то перед началом решения ее необходимо сбалансировать, введя недостающее число фиктивных строчек или столбцов с достаточно большими штрафными стоимостями работ.
|
|
|
Для решения данной задачи сначала построим ее математическую модель. Обозначим символом Хij переменную, имеющую только два допустимых значения: 0 или 1. Такие переменные называются двоичными. Причем, будем считать, что:
− Хij = 1, если i-ым рабочим выполняется j-ая работа;
− Хij = 0, если i-ым рабочим не выполняется j-ая работа.
Тогда математическую модель задачи о назначении можно сформулировать следующим образом:
минимизировать

при ограничениях

Для решения этой задачи с помощью средства Поиск решения необходимо выполнить некоторые предварительные действия:
1. В ячейки диапазона А2: D5 введите стоимости работ.
2. Отведите ячейки диапазона F2: I5 под неизвестные.
3. Введите в ячейку J1 функцию цели, вычисляющую стоимость работ:
=СУММПРОИЗВ(А2: D5; F2: I5)
4. В ячейки диапазонов J2: J5 и F6: I6 введите формулы, задающие левые части ограничений и представленные в следующей ниже таблице.
Ячейка Формула Ячейка Формула
J2 =CYMM(F2: I2) F6 =CYMM(F2: F5)
J3 =СУMM(F3: I3) G6 =СУММ(G2: G5)
J4 =CYMM(F4: I4) H6 =СУММ(Н2: Н5)
J5 =CУMM(F5: I5) I6 =СУММ(12: 15)

Рис. 7. 10. исходные данные задачи о назначении и заполненное диалоговое окно Поиск решения

Рис. 7. 11. Оптимальное решение задачи о назначении
Теперь все готово для поиска решения при помощи средства Поиск решения.
1. Выберите команду Сервис – Поиск решения и заполните диалоговое окно Поиск решения, как показано на рис. 7. 10.
2. Нажмите кнопку Выполнить. Средство Поиск решения найдет оптимальный план назначений на работы (рис. 7. 11).
|
|
|
7. 5. Расходы на маркетинг и рекламу
Условие задачи: какими должны быть расходы на маркетинг и рекламу, чтобы годовой бюджет стал равным 500000 долл. При стоимости каждого проекта 50000 долл.?
Создадим следующую таблицу:
| Стоимость производства | Накладные расходы | Маркетинг | Реклама | Стоимость проекта | |
| Проект 1 | |||||
| Проект 2 | |||||
| Проект 3 | |||||
| Проект 4 | |||||
| Проект 5 | |||||
| Проект 6 | |||||
| Проект 7 | |||||
| Проект 8 | |||||
| Проект 9 | |||||
| Проект 10 | |||||
| Годовой бюджет | |||||
Ограничения:
| Стоимость проекта равна | |
| Расходы на маркетинг (не менее, чем) | |
| Годовой бюджет не должен превышать |
Стоимость каждого проекта рассчитывается как сумма Стоимости производства, Накладных расходов, Маркетинга, Рекламы. Годовой бюджет равен сумме Стоимостей всех проектов.
Скопируем таблицу на другой лист книги и выполним команду Сервис – Поиск решения. В диалоговом окне установим ограничения, как показано на рис. 7. 12. После этого нажмем кнопку Выполнить. Результат решения задачи приведен на рис. 7. 13.
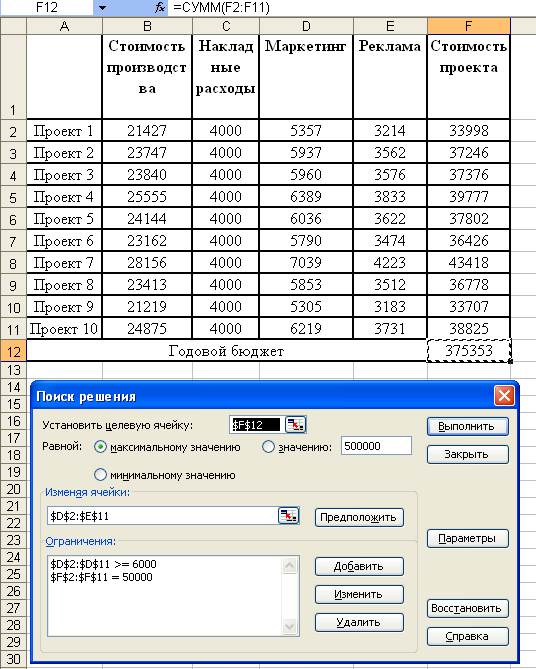
Рис. 7. 12. Исходные данные к задаче и задание ограничений

Рис. 7. 13. Решение задачи с помощью Поиска решения
|
|
|


