 |
=CYMM(F3:F8).. Таблица 7.3
|
|
|
|
=В2;
• в ячейку D4 введите формулу
=D3+0. 9*B3;
• выберите ячейку D4, расположите указатель мыши на ее маркере авзаполнения и протяните его вниз на диапазон D5: D8. Теперь, в ячейках диапазона D3: D8 будем вычислять число постоянно работающих стюардесс в текущем месяце.
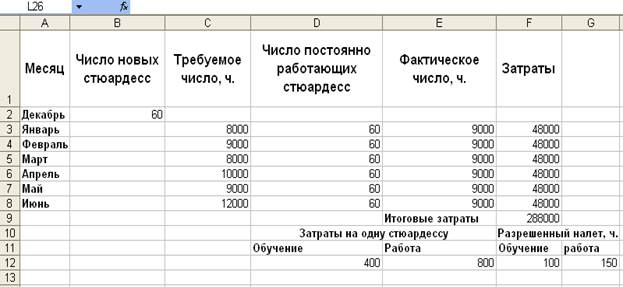
Рис. 7. 4. Исходные данные задачи о штатном расписании
4. В ячейках диапазона ЕЗ: Е8 вычислим налет по месяцам. Для этого:
введите в ячейку Е3 формулу
=D3*$G$12+B3*$F$12
• где в ячейки F12 и G12 введен допустимый налет обучаемой и работающей стюардессы.
• выберите ячейку Е3, расположите указатель мыши на ее маркере авзаполнения и протяните его вниз на диапазон Е4: Е8. Теперь, в ячейках диапазона ЕЗ: Е8 будет вычисляться налет по месяцам.
5. В ячейках диапазона F3: F8 вычислим затраты по месяцам. Для этого:
• введите в ячейку F3 формулу
=D3*$E$12+B3*$D$12
где в ячейки D12 и Е12 введены зарплата обучающейся и работающей стюардессы;
• выберите ячейку F3, расположите указатель мыши на ее маркере авзаполнения и протяните его на диапазон F4: F8.
6. Осталось только вычислить суммарные затраты за планируемый период. Для этого в ячейку F9 введите формулу
=CYMM(F3: F8).
Теперь все готово для решения задачи о составлении штатного расписания при помощи средства Поиск решения.
1. Выберите команду Сервис – Поиск решения.
2. На экране отобразится диалоговое окно Поиск решения. Заполните диалоговое окно Поиск решения, как показано на рис. 7. 5.
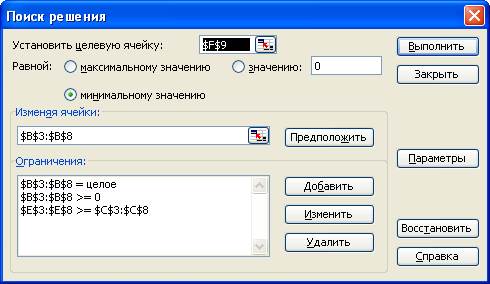
Рис. 7. 5. Окно команды Поиск решения в задаче о штатном расписании
Результаты расчета оптимального штата стюардесс приведены на рис. 7. 6.
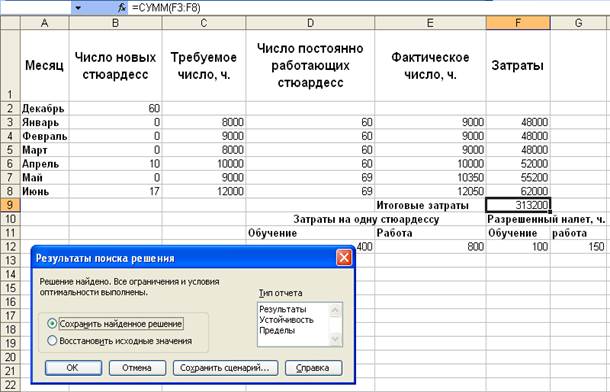
Рис. 7. 6. Найденное решение задачи о штатном расписании
7. 3. Транспортная задача 
|
|
|
Рассмотрим еще один пример применения средства Поиск решения. Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики располагаются в Денвере, Бостоне, Нью-Орлеане и Далласе с производственными возможностями соответственно 200, 150, 225 и 175 единиц продукции ежедневно. Распределительные центры располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике не поставленной в центр распределения единицы продукции обходится в $0, 75 в день, а штраф за просрочку поставки заказанной потребителем в центре распределения единицы продукции, но там не находящейся, равен $2, 5 в день. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в табл. 7. 3.
Таблица 7. 3
Транспортные расходы
| Лос-Анджелес | Даллас | Сент-Луис | Вашингтон | Атланта | Производство | |
| 1 Денвер | 1, 5 | 1, 75 | 2, 25 | 2, 25 | ||
| 2 Бостон | 2, 5 | 1, 75 | 1, 5 | |||
| 3 Нью-Орлеан | 1, 5 | 1, 5 | 1, 75 | 1, 75 | ||
| 4 Даллас | 0, 5 | 1, 75 | 1, 75 | 1, 75 | ||
| Потребность |
Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.
Для решения данной задачи построим ее математическую модель. Неизвестными здесь являются объемы перевозок: Пусть хij — объем перевозок с i-ой фабрики в j-ый центр распределения. Функцией цели являются суммарные транспортные расходы, т. е.

где сij — стоимость перевозки единицы продукции с с i-ой фабрики в j-ый центр распределения. Кроме того, неизвестные должны удовлетворять следующим ограничениям:
− неотрицательность объема перевозок;
− т. к. модель сбалансирована, то вся продукция должна быть вывезена с фабрик, и потребность всех центров распределения должна быть полностью удовлетворена.
|
|
|
Таким образом, мы имеем следующую модель:
минимизировать 
при ограничениях:
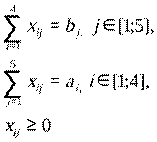
где аi – объем производства на i-ой фабрике; bj – спрос в j-ом центре распределения.
Выполните следующую подготовительную работу для решения транспортной задачи с помощью средства Поиск решения (рис. 7. 7).
1. Введите в ячейки диапазона В3: F6 стоимости перевозок.
2. Отведите ячейки диапазона В8: F11 под значения неизвестных (объемов перевозок).
3. Введите в ячейки диапазона Н8: Н11 объемы производства на фабриках.
4. Введите в ячейки диапазона В13: F13 потребность в продукции в пунктах распределения.
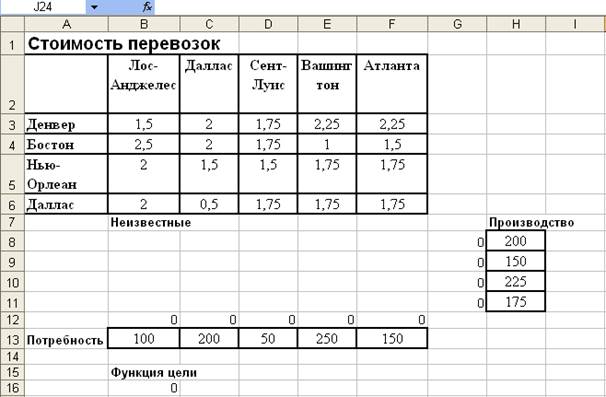
Рис. 7. 7. Исходные данные для транспортной задачи
111232896. В ячейку В16 введите функцию цели
|
|
|


