 |
1.Модели в экономике и других науках.
|
|
|
|
1. Модели в экономике и других науках.
Выделяют три основных типа экономических моделей.
1)Регрессионыые модели.
Представляют собой одно уравнение парной регрессии или множественной регрессии.
Парная регрессия: уравнения вида y=f(x), где x-независимая переменная, y-зависимая переменная
2)системы одновременных (эконометрических) уравнений
3)временные ряды.
Типы данных, которые используются при составлении моделей обычно делят на два:
1. пространственные данные
2. данные, связанные с фактором времени(временные)
При исследовании различных моделей исходные данные анализируются и обрабатываются с целью дальнейшего использования при прогнозе. Для этого используются следующие виды анализа данных:
1)дисперсионный анализ - позволяет определить факт влияния одного или нескольких факторов(переменных) на результативный признак.
2)корреляционный анализ – позволяет определить тесноту связи между двумя или более факторами.
3)регрессионный анализ – позволяет установить количественную зависимость между двумя или более факторами в виде 1ого регрессионного уравнения или системы уравнений.
4)анализ временных рядов позволяет выявить структуру ряда, т. е. определить количественные значения характеристик, формирующих уровень ряда.
2. Модель парной регрессии. Подбор кривой.
Основной задачей регрессионного анализа является определение зависимостей между двумя или более величинами, которые выражаются в виде уравнений или систем уравнений. Если исследуется связь между двумя факторами, то уравнения называются парной регрессии.
Парная регрессия: уравнения вида y=f(x), где x-независимая переменная, y-зависимая переменная(результативный признак)
|
|
|
Используется таблица, где
| x | X1 | … | xn |
| y | Y1 | … | y |
Таблица фактических значений
Можно графически изобразить фактические значения X и y.
y 
b> 0 yпрmin
Xпр-прогнозное
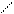
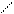
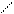
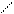yпр max
 |
(x; y) Xпр x
Линия регрессии 
-теоретическая линия.
Парная регрессия: 1)линейная, тогда 
a, b-числовые коэф-ты. параметры уравнения регрессии. b=tgα (является определяющим)
2)нелинейная
а) 
-парабола
б)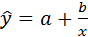 
-гипербола
в)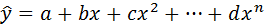 
- полиномиальная кривая
Целью исследования является определение или оценка параметров уравнения регрессии.
Чаще всего для оценки параметров уравнения регрессии используется метод наименьших квадратов (МНК)
3. Регрессия по методу наименьших квадратов.
Чаще всего для оценки параметров уравнения регрессии используется метод наименьших квадратов (МНК)
Суть МНК- составляется функция(целевая), которая представляет собой сумму квардатов отклонений фактических значений от теоретических х. Эта функция должна быть минимальны (т. е. необходимо, чтобы сумма квадратов расстояний между теоретическими и фактическими значениями была минимальной).
F(a, b) 
Мы должны получить такое значение а и b, чтобы фактические значения находились как можно ближе к теоретическим.
Решается оптимальная задача, Функция непрерывна и диф-ма. Используются классические методы оптимизации. (нахождение функции по 2м экстремумам) Составляется сис-ма уравнений из частных производных, которые приравниваются к 0
|
|
|
Необходимое условие существования экстремума.
- делим на n- получаем новую систему.
; 
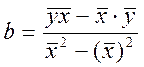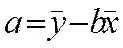; y=a+b*x
Необходимо найти такую пару чисел, которая позволяет провести такую линию, чтобы отклонения фактических значений от теоретических были минимальны.
|
|
|
