 |
4. Интерпретация уравнения регрессии.
|
|
|
|
4. Интерпретация уравнения регрессии.
Чаще всего для оценки параметров уравнения регрессии используется метод наименьших квадратов (МНК)
Суть МНК- составляется функция(целевая), которая представляет собой сумму квардатов отклонений фактических значений от теоретических х. Эта функция должна быть минимальны (т. е. необходимо, чтобы сумма квадратов расстояний между теоретическими и фактическими значениями была минимальной).
F(a, b) 
Мы должны получить такое значение а и b, чтобы фактические значения находились как можно ближе к теоретическим.
; 
;
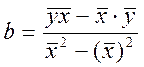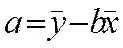Уравнение регрессии. y=a+b*x
a, b-числовые коэф-ты. параметры уравнения регрессии. b=tgα (является определяющим)-это тангенс угла наклона прямой, образованного с положительным направлением оси Ох.
Коэффициент а показывает значение показателя у при х=0, это расстояние на которое сдвигается прямая относительно Ох.
y
y=a+b*x
а у=а
α
x
5. Качество оценки.
Для оценки качества построенной модели можно использовать следующие показатели:
-относительная ошибка аппроксимации,
-коэффициент детерминации,
- коэффициент корреляции.
Средняя ошибка аппроксимации. Это среднее отклонение расчётных значений от фактических:
|
|
|
, y- фактическое значение, ŷ - прогнозное (теоритическое) значение. Допустимый предел значения средней апроксимациии- не более 8-10%.
Коэффициент детерминации.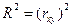 
Показывает на сколько % изменения показателя у от своего среднего значения зависит от изменения фактора х от своего среднего значения. Чем ближе значение R² к 1, тем точнее модель.
Из всех полученных уровнений регрессии, лучшей является та, у которой коэф-т детерминации больший.
Коэффициент корреляции. определяет степень линейной связи.
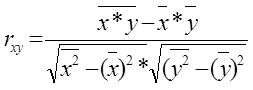
6. Свойства коэффициентов регрессии.
Уравнения вида y=f(x), где х-независимая переменная; у-зависимая переменная(результативный признак) наз-ся уравнениями парной регрессии. Используется таблица, где
| х | Х1 | ……. | Хn |
| у | У1 | …….. | уn |
Это можно изобразить на графике
Хпр-прогнозное значение х
Yпрmin, max минимальное и максимальное значение прогнозного у.
Парная регрессия
- линейная, когда y^=a+b*x, с числовыми к-тами а и b –параметры уравнения регрессии, b=tg α. (тангенс угла наклонной оси х); а-показывает значения показателя у при нулевом значении х.
- нелинейная, y=a+bx+cx^2(парабола)
y=a+b/x (гипербола); y(с домиком)=a+bx+cx^2+…+dx^n-полиномиальная кривая
• Коэффициент регрессии принимает любые значения.
• Коэффициент регрессии не симметричен, т. е. изменяется, если X и Y поменять местами.
• Единицей измерения коэффициента регрессии является отношение единицы измерения Y к единице измерения
X - ([ Y ] / [ X ]).
• Коэффициент регрессии изменяется при изменении единиц измерения X и Y.
7. Проверка гипотез.
Для оценки адекватности построенной модели используется метод проверки гипотез.
Выдвигается нулевая гипотеза Н0, в кот. делается предположение от том, что между факторами х и у нет никакой связи, т. е. уравнение регрессии статистически не значимо, т. е. его нельзя использовать для прогноза.
Н0: rxy=0, а=0, b=0.
Для проверки нулевой гипотезы используется t-критерий Стьюдента.
При больших объемах выборок (n> 30) закон распределения Стьюдента приближается к нормальному закону распределения. (графики)
|
|
|
P(t)
t H0=99%
Для проверки нулевой гипотезы сравнивают фактическое значение t и критическое. Критическое значение определяется по спец таблицам в зависимости от колчества данных и уровня значимости.
Если tфакт< tкрит, то Н0 принимается, и это означает, что уравнение регрессии стат незначимо и его нельзя использовать для прогноза. И наоборот.
Можно оценить стат значимость каждого уравнения регрессии в отдельности для этого рассчит-ся tкритериев для каждого параметра.
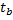=b/mb; 
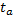=a/ma; 
=r/mr
ma, mb, mr-случайные ошибки; ma=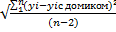 
* 
; mbтоже самое только * на 
; mr= 
; H01: b=0; H02: a=0; H03: 
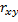=0
tb< tq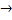 
H01 принимается; ta< tq H02 принимается; tr< tq H03принимается ЕСЛИ ВСЕ ЭТИ ЗНАЧЕНИЯ 
tq H0 отвергается.
Проверка гипотез в регрессионном анализе. Выдвигается нулевая гипотеза Н0, в кот. делается предположение, что между факторами х и у нет никакой связи, т. е. ур-ние регрессии стат незначимо и его нельзя исп-ть для прогноза. rxy=0, a=0, b=0. n> 30) p-y распределения Стьюдента приближается к нормальному з-ну распределения. См график. 
, F=t^2. (связь между критерием Стьюдента и крит Фишера)
РИСУНОК!!!! СВЯЗЬ КРИТЕРИЕВ!!!
Под кривой распределения область делится на 2 части:
I-ОДЗ, II- критическася область. Для проверки нулевой гипотезы сравнивают фактическое значение t и критическое. Критич. Значение определяется по спец. Таблицам в зависимости от количества данных и уровня занчимости. Если t факт < t крит, то Н0 принимается и это означает, что ур-ние регрессии стат незначимо и его нельзя исп-ть для прогноза. Если наоборот, то Н0 отвергается и можно сделать выо о том, что ур-ние регрессии получено не случайным образом, оно стат значимо и его можно исп-ть для прогноза.
Проверка гипотез в дисперсионном анализе. Проверка гипотез в дисперсионном анализе происходит с помощью F-кртиерия Фишера. Для этого выполняется сравнение фактического Fфакт и критического значений F-критерия Фишера. Fфакт определяется из соотношения значений межгрупповой и внутригрупповой дисперсии: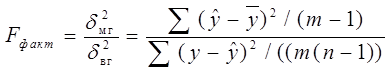 
,
|
|
|
РИСУНОК!!! РАСПРЕДЕЛЕНИЕ ФИШЕРА!!!
n- измерений, m-групп.
Fтабл - это максимально возможное значение критерия под влиянием случайных факторов
при данных степенях свободы и уровне значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимают равной 0, 005 или 0, 01.
Если Fфакт< Fq, то это означает, что расчетные значения случ. Величины f попадают в I-ую область, т. е. Н0 принимается или подтверждается и делается вывод о том, что фактор х не влияет ан показатель у, и признается надежность ур-ния. Если наоборот, то для заданного уровня значимости q расчетные значения критерия Фишера F попадают во II область и поэтому Н0 отвергается и принимается решение о том, что фактор х влияет на показатель у.
|
|
|
