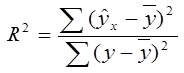|
11. Тесты на качество оценивания.
|
|
|
|
11. Тесты на качество оценивания.
Для оценки адекв-ти построенной модели исп. метод проверки гипотез.
Выдвигается нулевая гипотеза Н0, в кот. делается предположение от том, что между факторами х и у нет никакой связи, т. е. уравнение регрессии статистически не значимо, т. е. его нельзя использовать для прогноза.
Н0: rxy=0, а=0, b=0.
Для проверки нулевой гипотезы используется t-критерий Стьюдента.
При больших объемах выборок (n> 30) закон распределения Стьюдента приближается к нормальному закону распределения. (графики)
P(t)
 t H0=99%
t H0=99%
Для проверки нулевой гипотезы сравнивают фактическое значение t и критическое. Критическое значение определяется по спец таблицам в зависимости от количества данных и уровня значимости.
Если tфакт< tкрит, то Н0 принимается, и это означает, что уравнение регрессии стат. незначимо и его нельзя использовать для прогноза. И наоборот.
Можно оценить стат. значимость каждого уравнения регрессии в отдельности для этого рассчит-ся t-критериев для каждого параметра.
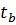 =b/mb;
=b/mb; 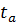 =a/ma;
=a/ma; 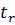 =r/mr
=r/mr
ma, mb, mr-случайные ошибки; ma=  *
* 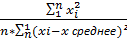 ; mbтоже самое только * на
; mbтоже самое только * на  ; mr=
; mr=  ; H01: b=0; H02: a=0; H03:
; H01: b=0; H02: a=0; H03: 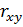 =0
=0
tb< tq  H01 принимается; ta< tq, то H02 принимается; tr< tq H03принимается ЕСЛИ ВСЕ ЭТИ ЗНАЧЕНИЯ
H01 принимается; ta< tq, то H02 принимается; tr< tq H03принимается ЕСЛИ ВСЕ ЭТИ ЗНАЧЕНИЯ 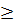 tq, то H0 отвергается.
tq, то H0 отвергается.
Проверка гипотез в регрессионном анализе. Выдвигается нулевая гипотеза Н0, в кот. делается предположение, что между факторами х и у нет никакой связи, т. е. ур-ние регрессии стат незначимо и его нельзя исп-ть для прогноза. rxy=0, a=0, b=0. n> 30) p-y распределения Стьюдента приближается к нормальному з-ну распределения. См график.  , F=t^2. (связь между критерием Стьюдента и крит Фишера)
, F=t^2. (связь между критерием Стьюдента и крит Фишера)
РИСУНОК!!!! СВЯЗЬ КРИТЕРИЕВ!!!
Под кривой распределения область делится на 2 части:
|
|
|
I-ОДЗ, II- критическая область. Для проверки нулевой гипотезы сравнивают фактическое значение t и критическое. Критич. значение определяется по спец. Таблицам в зависимости от количества данных и уровня значимости. Если t факт < t крит, то Н0 принимается и это означает, что ур-ние регрессии стат незначимо и его нельзя исп-ть для прогноза. Если наоборот, то Н0 отвергается и можно сделать выо о том, что ур-ние регрессии получено не случайным образом, оно стат значимо и его можно исп-ть для прогноза.
Проверка гипотез в дисперсионном анализе. Проверка гипотез в дисперсионном анализе происходит с помощью F-критерия Фишера. Для этого выполняется сравнение фактического Fфакт и критического значений F-критерия Фишера. Fфакт определяется из соотношения значений межгрупповой и внутригрупповой дисперсии:  ,
,
РИСУНОК!!! РАСПРЕДЕЛЕНИЕ ФИШЕРА!!!
n- измерений, m-групп.
Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимают равной 0, 005 или 0, 01.
Если Fфакт< Fq, то это означает, что расчетные значения случ. Величины f попадают в I-ую область, т. е. Н0 принимается или подтверждается и делается вывод о том, что фактор х не влияет на показатель у, и признается надежность ур-ния. или наоборот.. Но отвергается
12. Анализ вариации зависимой переменной в регрессии.
Для определения показателя У(%) при изменении среднего значения Х на 1% используется коэффициент эластичности.
 -эластичность
-эластичность
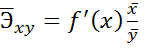 (%)
(%)
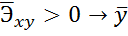 увеличивается;
увеличивается;
 уменьшается.
уменьшается.
Для парной регрессии:
 .
.
Для множественной регрессии:
Для определения силы влияния Х на У также используется показатель эластичности.
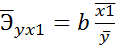

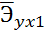 сравнивается с
сравнивается с 
Большему значению коэффициента эластичности соответствует большее влияние фактора У от Х.
|
|
|
|
13) Коэффициент детерминации | |||||||
| Долю диспресии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации R2: | |||||||
|
|
|
|
|
| |||
|
|
| Коэффициент детерминации-это квадрат коэффициента корелляции. | |||||
| Ŷ - пргнозное(теоретическое) значение y |
|
|
|
|
| ||
| ŷ x=a-bx |
|
|
| ||||
|
|
|
| |||||
|
|
|
| |||||
|
|
|
| |||||
|
|
|
| |||||
| Его значение показывает, на сколько % изменение показателя у зависит от изменения х. | |||||||
|
|
|