18. Проверка статистических гипотез.

18. Проверка статистических гипотез.

     Для оценки адекватности модели множественной регрессии используется критерий Фишера.

F(критерий) параметр Фишера

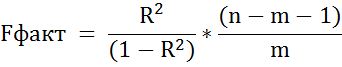
где  - коэффициент детерминации, показывающий на сколько процентов изменение показателя y зависит от изменения факторов X1, X2

m – количество факторов xj; n – количество измерений.

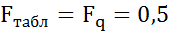
1) Если Fфакт < Fтабл

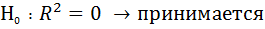
Нулевая гипотеза в которой предполагается что уравнение регрессии статистически незначимо принимается. Уравнение регрессии нельзя использовать для прогноза.

2) Если Fфакт ≥ F табл

.

Уравнение статистически значимо, его можно использовать для прогноза.

 

19. Мультиколлинеарность данных.

Если в уравнении множественной регрессии коэффициент корреляции между формулами r_xiхj ≥ 0, 7, то в построенной модели множественной регрессии присутствует явление мультиколлинеарности, т. е. факторы сильно влияют друг на друга, в результате чего искажается значение показателя у. Прежде чем выбрать основные факторы для уравнения множественной регрессии, необходимо рассчитать все возможные коэффициенты корреляции и построить корреляционную матрицу. В качестве основных факторов, которые включаются в модель, выбираются также те, у которых минимальные коэффициенты корреляции (мало отличительны от 0).

 # y=a+b₁x₁+b₂x₂, если r_xiхj ≥ 0, 7

                x₁                x₂              y

x₁    r_x1х1=1          r_x1х2                  r_xiy

R = x₂    r_x2х1             r_x2х2=1           r_xiy

y     r_yх1                    r_yх2                  r_yy=1

 

 

20. Временные ряды.

Временной (Динамический) ряд – совокупность различных значений одного объекта за ряд последовательных моментов или периодов времени.

Временные ряды бывают – дискретными – такой ряд в котором какие любо характеристики объекта определяются в определенный момент времени.

Например:

t	01. 01	02. 01.	03. 01
Y(t)	28, 9	28, 6	29, 8

Y(t) – характеристика объекта – уровень ряда на момент t.

Интервальные - связаны с накоплением (суммой) величины за равные промежутки времени

ti – ti+1	01. 01-01. 02	02. 02-01. 03	02. 03-01. 04
yt	4%	5%	6%

Значение уровнения ряда у(t) формируется под воздействием факторов:

1) Факторы, формирующие тенденцию ряда – называются Трендовые компоненты – Т.

а) К возрастанию б) К убыванию

2)Факторы формирующие циклические или сезонные колебания –S. Сезонная или циклическая компонента.

3) Случайные факторы Е                         

                                                    Влияние Т, S                        Влияние Е

                                                                                                                                

            Основной задачей исследования временного ряда является определение и выявление каждой из компонент составляющих уравнение ряда.

            Поэтому задачей исследования является выявление количества компонентов и определения их значения в каждый (Момент) период времени.

Обычно для составления временного ряда используют модели двух видов:

1) Аддитивная модель Y=T+S+E

2) Мультипликативная модель Y=T*S*E

Если амплитуда колебания ур-я ряда не меняется то используется Аддитивная модель, если изменяется ( Увелич. или уменьш. ) то используют мультипликативную модель.

21. Коэффициенты автокорреляции.

При наличии тенденции и циклических колебаний каждый последующий уровень ряда зависит от предыдущего. Количественное выражение степени связи уровней ряда за один или несколько периодов времени наз. коэффициентом автокорреляции. Они бывают 1-ого, 2, 3 и т. д. порядка.

Коэффициент автокорреляции показывает тесноту связи между уровнями ряда, сдвинутыми на 1 или более шаг.

Предположим, что значения y_t в текущем году зависят от значений в прошлом году, тогда значения в предыдущем году можно рассчитать с помощью коэффициента автокорреляции:

 

 

n -количество данных

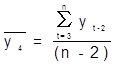
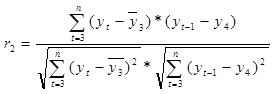r₁-коэффициент автокорреляции 1го порядка

 

Автокорреляция даёт информацию о наличии фактора, формирующего тенденцию ряда.

Полученные значения коэффициента автокорреляции 1го и 2го порядков свидетельствует о тесноте зависимости между текущими уровнями ряда и уровнями ряда предыдущих периодов, а также свидетельствует о линейной тенденции. Периоды, по которым рассчитывается коэффициент автокорреляции называются лагами. Для статистической достоверности коэффициента автокорреляции максимальный лаг может быть n/4.

Свойства коэффициента автокорреляции:

- характеризует только тесноту линейной связи текущего и предыдущего уровней ряда

- в случае нелинейной тенденции коэффициент автокорреляции может быть равен нулю

-по знаку коэффициента автокорреляции нельзя сделать вывод о возрастающей или убывающей тенденции.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: