 |
22. Корреляционная функция.. 25. Мультипликативная модель временного ряда.
|
|
|
|
22. Корреляционная функция.
Последовательность коэффициентов автокорреляции называется автокорреляционной функцией. График зависимости ее значений от величины коэффициентов автокорреляции(порядков коэффициентов автокорреляции) называют коррелограммой. Анализ автокорреляционной функции и коррелограммы позволяет определить структуру временного ряда. Если наиболее высоким оказывается коэффициент автокорреляции 1-го порядка – это означает, что временный ряд содержит тенденцию Т, если наиболее высоким оказался коэффициент автокорреляции τ -ого порядка – это означает, что временной ряд содержит сезонную или циклическую компоненту S с периодичностью τ моментов времени.
Если ни один из коэффициентов автокорреляции не оказался значимым, то это означает, что ряд не содержит ни тенденции, ни сезонных или циклических колебаний и требует дополнительных исследований. В этом случае действует случайная компонента или помехи, или имеет место нелинейная зависимость.
 |  | |||||||||
 | ||||||||||
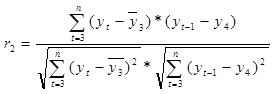 | ||||||||||
 | ||||||||||
 | ||||||||||
Анализ автокорреляционной функции позволяет сделать вывод о том, что в изучаемом временном ряде имеется тенденция T (к возрастанию или убыванию), сезонные колебания с расчётной периодичностью.
23. Определение тенденции временного ряда.
Одним из наиболее распространенных способов является построение аналитической функции, характеризующей зависимость уровней ряда от времени. Такая аналитическая функция называется трендом Т.
Определение аналитической функции называется выравниванием временного ряда.
Для построения тренда чаще всего используют следующие (элементарные) функции:
|
|
|
- линейная уt = a + bt T =a + bt - линейный тренд
-нелинейная:
а) полиномиальная yt=a+bt+ct2+…+ktn
б) степенная
в) показательная
a, b, c - параметры линии тренда
Если присутствует большой размах колебаний уровней ряда необходимо провести процедуру, которая называется сглаживание уровней временного ряда.
24. Аддитивная модель временного ряда.
Для выявления структуры временного ряда, т. е. определения количественных значений компонентов, составляющих уровней ряда, чаще всего используют аддитивную или мультипликативную модели временных рядов.
Аддитивная модель: У=Т+S+E,
T-трендовая компонента
S-сезонная компонента
E-случайная компонента
Аддитивная модель временного ряда используется в случае, если амплитуда сезонных колебаний практически не меняется. При этом предполагается, что все сезонные компоненты являются постоянными для различных типов.
Алгоритм построения модели. Процесс построения модели включает в себя следующие шаги:
1. Выравнивание уровней исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S
3. Устранение сезонной компоненты из исходного уровня ряда и получение выровненных данных без S
4. Аналитическое выравнивание уровней ряда и расчет значений фактора Т
5. Расчет полученных значений (Т* S) для каждого уровня ряда
6. Расчет абсолютных или относительных ошибок модели.
(или 4. Определение тенденции временного ряда и уравнения тренда; 5. Расчет абсолютных или относительных ошибок модели. )
25. Мультипликативная модель временного ряда.
Для выявления структуры временного ряда, т. е. определения количественных значений компонентов, составляющих уровней ряда, чаще всего используют аддитивную или мультипликативную модели временных рядов.
Мультипликативная модель. У=Т*S*E
|
|
|
T-трендовая компонента
S-сезонная компонента
E-случайная компонента
Мультипликативная модель используется в случае, если амплитуда сезонных колебаний увеличивается или уменьшается.
Алгоритм построения модели. Процесс построения модели включает в себя следующие шаги:
1. Выравнивание уровней исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S
3. Устранение сезонной компоненты из исходного уровня ряда и получение выровненных данных без S
4. Аналитическое выравнивание уровней ряда и расчет значений фактора Т
5. Расчет полученных значений (Т* S) для каждого уровня ряда
6. Расчет абсолютных или относительных ошибок модели.
(или 4. Определение тенденции временного ряда и уравнения тренда; 5. Расчет абсолютных или относительных ошибок модели. )
|
|
|


