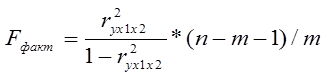|
14) Множественная (многомерная) регрессионная модель
|
|
|
|
14) Множественная (многомерная) регрессионная модель
Уравнение регрессии в стандартизированном виде:
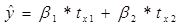
β определяет относительное влияние каждого фактора х на показатель у
 |  |
Они сравниваются по модулю. Большему коэффициенту соответствует большее влияние фактора х на показатель у. rxy1; rxy2; rxy3 - парные коэффициенты корелляции
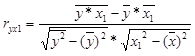 | |||||
 | |||||
 | |||||
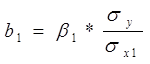
 Между коэффициентами β и параметрами b существует связь
Между коэффициентами β и параметрами b существует связь
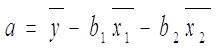 | |||||
 | |||||
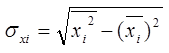 | |||||
 Множественный коэффициент корреляции рассч. для определения степени тесноты связи между всеми факторами
Множественный коэффициент корреляции рассч. для определения степени тесноты связи между всеми факторами
| Показывает на сколько изменеие показателя у зависит от изменения показателя х1 и х2 | ||
| Коэффициент детерминации показывает на сколько % изменение показателя у зависит от изменений фатора х1 х2 | ||
| R2=Rx1x2y2 | ||
| Криетрий Фишера: | ||
|
| ||
| m-колическтво факторов хj; n-колическтво измерений | ||||||
| Определяет статистическую значимость уровня регрессии. | ||||||
| Если Fтабл< Fфакт то гипотеза Hо отклоняется и признаётся статистическая | ||||||
| значимость и надёжность. | ||||||
| Средний коэффициент эластичности | ||||||
|
Показывает силу влияния одного показателя относительно другого на зависимую переменную, т. е. на сколько процентовв среднем по совокупности изменится результат у от своего среднего значения. Большему коэффициенту эластичности соответсвукт более сильное влияние фактора х на показатель у.
| ||||||
15) Основные гипотезы множественной регрессии
| Вся область всевозможных параметров f делится на 2-е части: | ||||||||
| 1) Область дорустимых значений, куда значения параметра f попадают с большей вер-тью | ||||||||
| > 90% |
|
| ||||||
| 2) Область критических значений: | ||||||||
| В качестве нулевой гипотезы Но выдвигается предположение о том, что все математические | ||||||||
| ожидания показателя отличаются друг от другого мало или равны: | ||||||||
| myi=my1=……=mym | ||||||||
| D качестве альтернативной гипотезы Н1 выдвигается предположение о том, что не все | ||||||||
| математические ожидания показателя равны между собой. | ||||||||
| Если принимается нулевая гипотеза, то все выделенные группы можно объединить в одну | ||||||||
| однородную группу и это означает, что рассматриваемые факторы не влияют на показатель У. | ||||||||
| Если принимается гипотеза Н1, то это означает, что результаты нельзя объединить в одну | ||||||||
| группу и поэтому считается, что факторы влияют на показатель групп. | ||||||||
| Для проверки гипотезы используется критерий Фишера для множественной регрессии: | ||||||||
| Криетрий Фишера: |
| |||||||
|
|
|
| ||||||
|
|
|
| ||||||
|
|
|
| ||||||
|
|
|
| ||||||
| Определяет статистическую значимость уровня регрессии. | ||||||||
| Если Fтабл< Fфакт то гипотеза Hо отклоняется и признаётся статистическая | ||||||||
| значимость и надёжность. | ||||||||
17) Свойства коэффициентов множественной регрессии.
Уравнение регрессии в стандартизированном виде.
I. Линейная  =a+
=a+ 
II. Нелинейная а)  =a+
=a+ 
б)  =a
=a 
Для определения степени влияния каждого фактора х на у используются коэффициенты 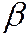 j, которые зависят от парных линейных коэффициентов корреляции.
j, которые зависят от парных линейных коэффициентов корреляции.
Например, для уравнения множественной регрессии рассчитываются коэффициенты 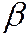 1 и
1 и 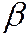 2:
2:
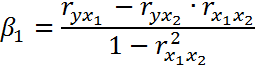

Затем они сравниваются по модулю. Большему β соответствует большее влияние фактора х на показатель у.
|
|
|
ryx1, ryx2, rx2x1 – парные коэффициенты корреляции:



0 – 0, 1 – Связь практически отсутствует
0, 1-0, 3 – Очень слабая 0, 3-0, 5 – Слабая 0, 5-0, 7 – Средняя
0, 7-0, 95 – сильная 0, 95-1 – Очень сильная
Между коэффициентами β и параметрами b существует связь:
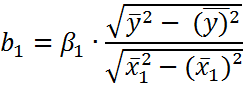

Для определения степени тесноты связи между всеми факторами рассчитывают множественный коэффициент корреляции.
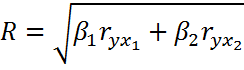

Коэффициент детерминации показывает насколько процентов изменение показателя у зависит от х1 и х2.
Для определения силы влияния факторов х на показатель у также используется показатель эластичности:


Т. е показывает на сколько % по совокупности изменяется пок-тель у, при изменения х на 1% от своего среднего значения.
|
|
|