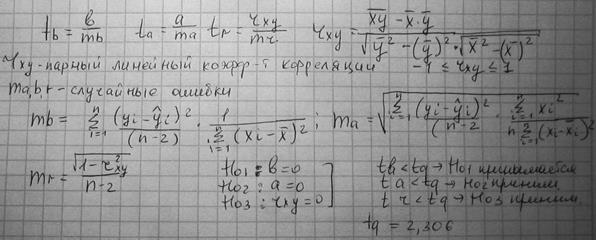|
8.Однофакторный дисперсионный анализ.
|
|
|
|
8. Однофакторный дисперсионный анализ.
Основной задачей дисперсионного анализа является выявление фактора влияния одного или нескольких факторов на показатель У. Пусть изучается влияние фатора х на показатель у. Для этого фиксируются рез-ты измерений показателя у в различных группах. Пусть для каждого фактора х выделяют m уровней и для каждого уровня проведено n измер. В качестве нулевой гипотезы выдвигается предположение о том, что показатель у не зависит от фактора х. В этом случае необходимо сравнить разброс значений результатов измерений у относительно средних значений в каждой группе, а также относительно общего среднего. Если эти отклонения не существенны, то нулевая гипотеза о равенстве мат ожиданий принимается: . Это означает, что результаты измерений не отличаются друг от друга и поэтому их можно объединить в одну однородную группу. Это означает, что фактор х не влияет на показатель у. Результаты измерения показателя у можно занести в след таблицу:
| № измерения | Группы (уровни) | |||||||||
| … | j | … | m | |||||||
| Y11 | Y12 | … | Y1j | … | Y1m | |||||
| Y21 | Y22 | … | Y2j | … | Y2m | |||||
| … | … | … | … | … | … | … | ||||
| i | Yi1 | Yi2 | … | yij | … | yim | ||||
| …. | … | … | … | … | … | … | ||||
| n | Yn1 | Yn2 | … | ynj | … | ynm | ||||
| Ср. в гр. |
|
|
|
| ||||||
| общ. Ср. |
| |||||||||
Среднее значение в каждой группе определяется по формуле: 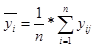 .
.
общее среднее: 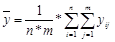 Н0=у1 среднее=у2 среднее=…. ymсреднее.
Н0=у1 среднее=у2 среднее=…. ymсреднее.
Разброс средних значений по группе результатов измерений и общего среднего можно оценить с помощью следующей формулы: Q=Q1+Q2, где Q- сумма квадратов отклонений результатов измерений от общего среднего, т. е. Q= 
|
|
|
Q1= 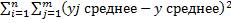 или Q1=n*
или Q1=n* 
Q2= 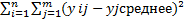
На самом деле, Q=Q1+Q2+Q3, но Q3=0. поэтому Q=Q1+Q2 где Q1 называется межгрупповой разброс средних значений. Q2 харктеризует разброс средних результатов значений У относительно среднего значения и называется внутригрупповым рассеиванием.
Число степеней свободы: Q1:  Q2:
Q2: 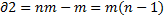
Для оценки дисперсии обозначим:
-Межгрупповая дисперсия: 
-Внутригрупповая дисперсия: 
Для проверки нулевой гипотезы Но можно использовать отношение 2-х дисперсий:  (эта величина подчиняется з-ну распределения Фишера)
(эта величина подчиняется з-ну распределения Фишера)
F параметр- Критерий Фишера. Обозначим все возможные значения F через f. Закон распределения Фишера: Вся область всевозможных параметров f делится на 2-е части: РИСУНОК РАСПРЕДЕЛЕНИЯ ФИШЕРА!!!!
1) Область допустимых значений, куда значения параметра f попадают с большей вероятностью > 90%
2) Область критических значений: p+q=1 p-попадающие в 90% q-не попадающие.
Вероятность попадания расчётного значения в критическую область назыв. уравнением значимости критерия фишера. Если Fрасч< Fкрит, то расчётное значение попадает в первую область допустимых значений, т. е. принимается нулевая гипотеза о равенстве математических ожиданий, и считается, что фактор х не влияет на у. Если наоборот, то для уровня значимости q расчетные значения критерия Фишера F попадают во II область и поэтому Н0 отвергается и принимается решение о том, что фактор х влияет на показатель у.
9. Двухфакторный дисперсионный анализ.
Дисперсионный анализ позволяет определить факторное влияние одного или нескольких факторов (переменных) на результативный признак. Рассмотрим случай, когда на пок-ль У влияют(или нет) 2 фактора. Предположим, что для каждого фактора производится только одно измерение. Тогда рез-ты измерений можно занести в след таблицу:
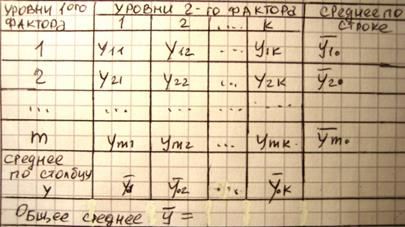
| Введем след. обозначения:
i-уровень фактора 1
j-уровень фактора 2
 = = 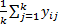 -среднее по i-ой строке -среднее по i-ой строке
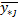 = =  -среднее по j-му столбцу -среднее по j-му столбцу
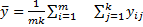 -общее среднее -общее среднее
|
Особенностью многофакторного анализа явл то, что взаимное влияние факторов может искажать рез-т показателей системы У. Общее отклонение любого рез-та измерения У от общего среднего склад-ся их 3-ех слагаемых Q=Q1+Q2+Q3, где Q1 хар-ет разброс рез-тов измерений(среднее по строке относительно общего среднего) Q1=k*  . Q2-квадратное отклонение средних по столбцу от общего среднего. Q2=m*
. Q2-квадратное отклонение средних по столбцу от общего среднего. Q2=m* 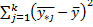 . Q3-остаточный разброс результатов измерения.
. Q3-остаточный разброс результатов измерения.  2. Q=
2. Q=  2. Для того, чтобы перейти к дисперсии нужно ввести число степеней свободы: для Q1:
2. Для того, чтобы перейти к дисперсии нужно ввести число степеней свободы: для Q1: 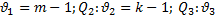 =
=
|
|
|
(m-1)(k-1). Тогда дисперсии можно оценивать по след. формулам:  .
. 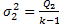 .
.
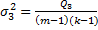 .
.  -дисперсия, хар-щая изменчивость средних значений У при изменении 1-ого фактора.
-дисперсия, хар-щая изменчивость средних значений У при изменении 1-ого фактора. 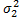 -хар-щая изменчивость средних значений У при изменении 2-ого фактора.
-хар-щая изменчивость средних значений У при изменении 2-ого фактора. 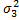 -определяет разброс величин У при исключении влияния 1-ого и 2-ого факторов.
-определяет разброс величин У при исключении влияния 1-ого и 2-ого факторов.
При двухфакторном дисперс. анализе требуется определить является ли существенным влияние 1-ого и 2-ого факторов на соответств. мат. ожидания У на фоне остаточного разброса, характеризуемого дисперсией 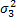 . Для этого проверяются 2 гепотезы:
. Для этого проверяются 2 гепотезы:
H01 заключается в том, что проверяется постоянство мат. ожиданий по строке при изменении 1-ого фактора. H02 о постоянстве мат ожиданий при изменении 2-ого фактора. Эти гепотезы проверяются с помощью критерия Фишера. F1ФАКТ=  , F2ФАКТ=
, F2ФАКТ= 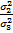 . По табл. Распределения Фишера в зависимости от ур-ния значимости Q и кол-ва строк и столбцов опред-ся критические знач-я F. (f1q, f2q).
. По табл. Распределения Фишера в зависимости от ур-ния значимости Q и кол-ва строк и столбцов опред-ся критические знач-я F. (f1q, f2q).
Если F1ФАКТ 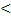 f1q, то принимается H01 и это означает, что 1-ый фактор не влияет на пок-ль У.
f1q, то принимается H01 и это означает, что 1-ый фактор не влияет на пок-ль У.
Если F1ФАКТ  f1q, то отклоняется H01 и это означает, что 1-ый фактор влияет на пок-ль У.
f1q, то отклоняется H01 и это означает, что 1-ый фактор влияет на пок-ль У.
Если F2ФАКТ  f2q, то принимается H02 и это означает, что 2-ой фактор не влияет на пок-ль У.
f2q, то принимается H02 и это означает, что 2-ой фактор не влияет на пок-ль У.
Если F2ФАКТ  f2q, то отклоняется H01 и это означает, что 2-ой фактор влияет на пок-ль У.
f2q, то отклоняется H01 и это означает, что 2-ой фактор влияет на пок-ль У.
Для определения степени линейной связи рассчитывается коэфф-т корреляции.
 , -1
, -1 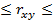 1.
1.
Для определения нелинейной связи определяется индекс корреляции
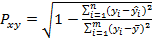 , 0
, 0 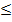
 1
1
Коэффициент детерминации: R2=  2-для лин связи. R2=
2-для лин связи. R2=  2-для нелин связи.
2-для нелин связи.
Показывает на сколько % изменения показателя у от своего среднего значения зависит от изменения фактора х от своего среднего значения. Чем ближе значение R² к 1, тем точнее модель.
|
|
|
Из всех полученных уровнений регрессии, лучшей является та, у которой коэф-т детерминации больший.

Если исследуется несколько факторов (больше2) то в этом случае рассчитывается множественный коэфф-т корреляции. RY, X1, X2.. XN-множественный коэфф-т корреляции.
При анализе влияния нескольких факторов друг на друга определяется корреляционная матрица, которая состоит из всех возможных парных линейных коэфф-тов корреляции.
Корреляционная матрица:

|
10. Доверительные интервалы. Уравнения вида y=f(x), где х-незав перем; у-зав. переменная (результативный признак) наз-ся уравнениями парной регрессии. Парная регрессия: - линейная, когда y^=a+b*x, с числовыми к-тами а и b –параметры уравнения регрессии, b=tg α. (тангенс угла наклонной оси х); а-показывает значения показателя у при нулевом значении х. - нелинейная, y=a+bx+cx^2(парабола) y=a+b/x (гипербола); y(с домиком)=a+bx+cx^2+…+dx^n-полином. кривая. Целью анализа явл опред-ие(оценка)параметров регрессии. Чаще всего исп-ся (мнк). Суть МНК в том, что составляется функция, кот представляет собой сумму квадратов отклонений фактических значений от теоретических. Эта функция должна быть минимальна. F(a, b)= b= Прогноз бывает 2-ух видов: 1)точечный Для определения доверительных интервалов и получения пар-ра упр, используются след формулы
|
|
|
|






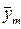

 , a=
, a= 
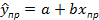 , где
, где  - 2)доверительный интервал:
- 2)доверительный интервал: 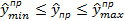 . Оценить стат. значимость можно у каждого параметра уравнения в отдельности. Для этого рассчит. t-критерии для каждого пар-ра.
. Оценить стат. значимость можно у каждого параметра уравнения в отдельности. Для этого рассчит. t-критерии для каждого пар-ра.