 |
Тема 3.7. Реактивные мощности по концам линии. Распределение параметров режима вдоль протяженной линии СВН
|
|
|
|
Тема 3. 7. Реактивные мощности по концам линии. Распределение параметров режима вдоль протяженной линии СВН
Реактивные мощности идеализированной линии
Расчетное выражение для определения значения реактивной мощности конца линии в зависимости от других параметров режима может быть получено из (3. 44). Перенеся в левую часть первого уравнения напряжение 
, получим
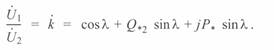
Возведя в квадрат левую и правую части этого уравнения, будем иметь
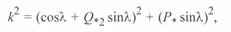
откуда может быть получено значение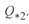 
. Выражение для определения реактивной мощности начала линии может быть получено из первого уравнения (3. 39). После проведения некоторых преобразований в результате будем иметь
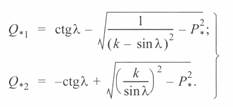(3. 62)
Выше говорилось, что в соответствии с круговой диаграммой каждому значению мощности 
соответствуют два значения мощности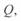 
, что выражается в двух знаках перед корнем 
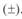. В уравнениях (3. 62) различные знаки перед корнем соответствуют условию 
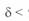90°. Оба уравнения выражены в относительных единицах. Важно отметить, что базисные условия для них различны. В первом уравнении базисная мощность определяется по напряжению 
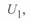, во втором — по напряжению 
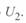. В практических расчетах удобнее применять единую базисную мощность. Обычно для этого используется мощность, определенная по напряжению конца линии 
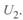. для получения расчетного выражения 
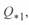, определенного через базисную мощность конца линии, можно воспользоваться уравнениями (3. 23) и (3. 56).
Ток в конце линии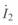 
может быть определен как
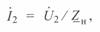
где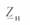 
— сопротивление эквивалентной нагрузки, включенной в конце линии.
Подставив это значение тока в первое уравнение (3. 25):
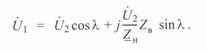
Представим отношение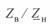 
как
|
|
|
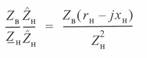
и подставив его в уравнение для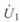 
, получим
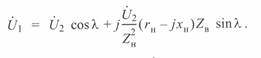
Подставив это выражение вместо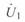 
в уравнение круговой диаграммы (3. 56), после преобразований получим:
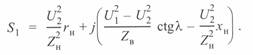(3. 63)
В этом уравнении действительная часть есть активная мощность конца линии, равная мощности нагрузки, а поскольку рассматривается идеализированная линия, она равна мощности начала линии, т. е. 
. Мнимая часть уравнения есть реактивная мощность начала линии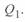 
. Она имеет две составляющие, причем вторая составляющая есть реактивная мощность нагрузки, т. е. реактивная мощность конца линии 
.
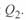Отсюда реактивная мощность начала линии может быть записана как
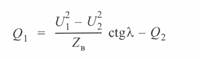
или
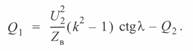(3. 64)
В относительных единицах это выражение имеет вид
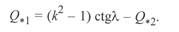(3. 65)
Подставив сюда значение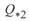 
из (3. 62), окончательно получим
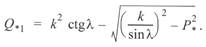(3. 66)
Здесь знак «минус» перед корнем отвечает условию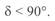 
.
Первая составляющая правой части уравнений (3. 64) и (3. 65) не является реактивной мощностью, которая определяется внутренними процессами в самой линии. Это так называемый сквозной переток реактивной мощности, который возникает лишь при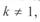 
, т. е. при наличии перепада напряжений по концам линии. Он создается двумя факторами. Первый и основной из них — это генерация реактивной мощности внешними по отношению к линии источниками: генераторами, синхронными компенсаторами и др. В результате этого повышается напряжение в узле, к которому подключено начало линии, за счет чего и возникает этот переток, например, от генераторов удаленной электростанции в приемную систему. При этом возникают дополнительные потери активной мощности в линии. Вопрос о целесообразности такого перетока следует рассматривать отдельно с учетом технико-экономических показателей.
Вторым, менее существенным, фактором является повышенная генерация реактивной мощности емкостью линии на участках, прилегающих к узлу с более высоким напряжением.
|
|
|
Качественная картина влияния перепада напряжений на распределение реактивной мощности по идеализированной линии приведена на рис. 3. 10. При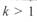 
, из-за сквозного перетока эпюра реактивной мощности смещается вверх от положения, имеющего место при 
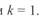. В результате при 
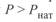увеличивается значение 
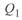и уменьшается значение 
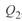, при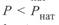 
снижается значение 
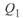и увеличивается значение 
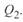. При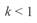 
направление сквозного перетока меняется на противоположное, соответственно меняется и его знак. Эпюра реактивной мощности смещается вниз от положения при 
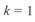с соответствующим изменением значени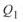й 
и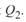 
.
Как следует из приведенных выше уравнений, сквозной переток является функцией длины линии. При относительно коротких линиях, когда значение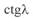 
достаточно велико, возникновение даже незначительного перепада напряжений может привести к большим сквозным перетокам реактивной мощности. Так, например, для линий 100 и 300 км при k = 1, 05 значения сквозных перетоков реактивной мощности 
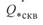составляют 0, 975 и 0, 315 соответственно.
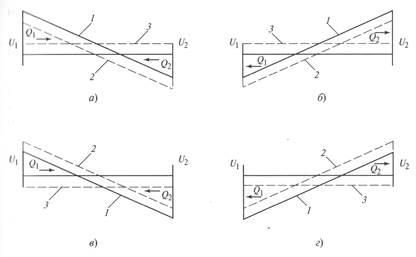
Рис. 3. 10. Влияние перепада напряжений на распределение реактивной мощности по идеализированной линии:
В первом случае сквозной переток практически равен натуральной мощности линии, что приводит к резкому возрастанию потерь активной мощности в ней и возможному нарушению баланса реактивных мощностей в ее приемном узле. На более длинной линии эти последствия будут также проявляться, но в меньшей степени. Все это требует принятия соответствующих мер по нормализации режима путем выбора оптимального значения перепада напряжений.
Уравнения (3. 66) и (3. 62) могут быть преобразованы следующим образом. Первый член правой части перенесем в левую часть, возведем обе части уравнений в квадрат и после преобразований получим:
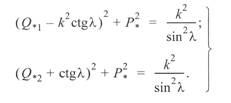(3. 67)
Уравнения (3. 67) также являются уравнениями круговых диаграмм идеализированной линии, записанными в несколько иной форме, чем уравнения, полученные выше. Это можно показать следующим образом.
Каноническое уравнение окружности, расположенной в первом квадранте в осях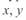 
имеет вид
(3. 68)
где 
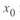и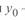 
— координаты центра; 
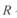— радиус окружности.
|
|
|
Сопоставив уравнения (3. 67) и (3. 68), можно видеть, что в (3. 67) смещения центра по оси абсцисс нет. Центр смещен только по оси ординат, причем отрицательный знак соответствует смещению по положительной полуоси ординат, положительный — по отрицательной. Иными словами, центр окружности начала линии смещен вверх, конца линии — вниз от центра координат, что было показано ранее.
|
|
|
