 |
Круговые диаграммы идеализированной линии
|
|
|
|
Для пояснения соотношения основных параметров режимов линии могут быть использованы круговые диаграммы. Для расчета режимов электропередач эти диаграммы обычно не используются вследствие малой точности графических методов решения, однако они удобны для пояснения физической сущности процессов, происходящих в линии при изменении передаваемой мощности и длины линии. Кроме того, уравнения круговых диаграмм позволяют получить некоторые расчетные выражения, которые могут быть использованы в практике.
Круговыми диаграммами называются зависимости активной и реактивной мощности начала и конца линии от угла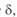 
, построенные в прямоугольных комплексных координатах 
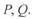. Воспользуемся уравнениями (3. 25). Найдя из первого уравнения ток 
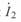и подставив его во второе, после преобразований получим прямой комплексный ток
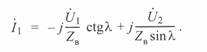(3. 54)
Сопряженный комплексный ток
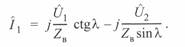(3. 55)
Полная мощность начала линии
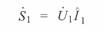
или
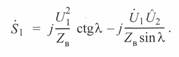(3. 56)
Положив 
, будем иметь 
, 
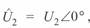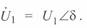. В этом случае уравнение круговой диаграммы начала линии имеет вид
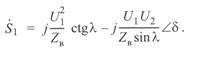(3. 57)
Как можно видеть из (3. 57), вектор полной мощности есть разность двух векторов:
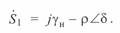
Эта диаграмма представлена на рис. 3. 8, а.
Конец вектора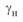 
определяет собой центр окружности, который для идеализированной линии расположен на мнимой оси. Координата этого центра определяется первым членом (3. 57). Значение модуля второго вектора определяется напряжениями по концам линии и её длиной. Этот вектор является радиусом окружности, его начало расположено в центре окружности, а его положение определяется углом 
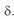. Таким образом, он является радиусом-вектором 
. При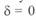 
он расположен вдоль мнимой оси и его конец направлен вниз. При увеличении электрического угла в пределах 0—360° этот конец описывает окружность, причем, поскольку вектор 
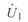— прямое комплексное напряжение, вращение радиуса происходит в положительном направлении, т. е. против часовой стрелки.
|
|
|
Проекции конца радиуса-вектора на оси действительных и мнимых величин определяют значения активной и реактивной мощности начала линии. Максимальная мощность, которую можно передать по линии (без учета коэффициента запаса по устойчивости),
соответствует 
, и поэтому численное значение радиуса-вектора определяет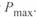 
.
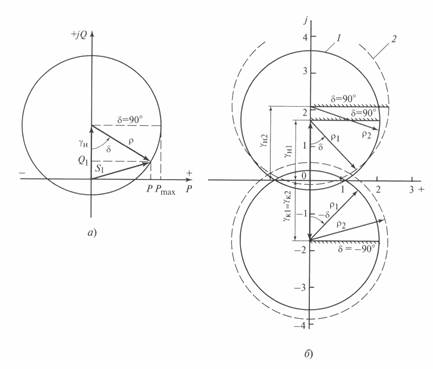
Рис. 3. 8. Круговые диаграммы некомпенсированной линии:
а — диаграмма начала линии; б — совмещенные диаграммы начала и конца линии при разных значениях перепада напряжений: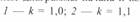 
Отметим, что каждому значению активной мощности на круговой диаграмме соответствуют два значения реактивной, однако рабочей является точка, лежащая в диапазоне изменения электрических углов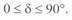 
.
Воспользовавшись уравнениями (3. 23) и проведя аналогичные преобразования, получим уравнение круговой диаграммы конца линии:
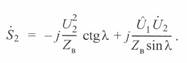(3. 58)
Пр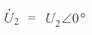и 
и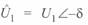 
окончательно имеем
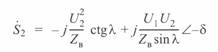(3. 59)
или
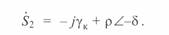
Круговые диаграммы линии могут быть записаны в относительных единицах. для этого введем величину перепада напряжений
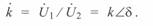(3. 60)
В общем виде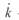 
— это вектор, однако для практических расчетов обычно его рассматривают как отношение модулей напряжени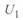й 
и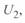 
, и сам он является модулем:
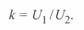
Учитывая, что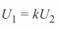 
и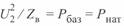 
, получаем:
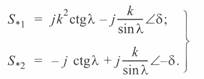(3. 61)
Совмещенные круговые диаграммы начала и конца некомпенсированной линии 500 кВ длиной 500 км при разных значениях перепада напряжений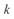 
приведены на рис. 3. 8. б. На этом рисунке круговые диаграммы даны в относительных единицах, индексом 1 обозначены величины, соответствующие 
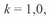, индексом 2 — 
.
|
|
|
Отметим следующие отличия круговых диаграмм конца линии от диаграмм ее начала:
- центры круговых диаграмм конца лини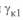и 
и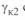 
смещены в отрицательную область мнимой оси координат, и численное значение их координат определяется длиной линии;
- отсчет угла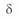 
для круговой диаграммы конца линии ведется в отрицательном направлении, т. е. по часовой стрелке;
- при равных напряжениях по концам линии 
центры окружностей начала и конца линии удалены на равные расстояния от начала координат 
; значения радиусов-векторов равны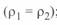 
;
- при наличии перепада напряжений на линии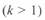 
центр круговой диаграммы начала линии 
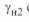смещается вверх по оси ординат, в то время как положение центра окружности конца линии 
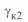не меняется (при условии, что напряжение 
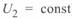). Одновременно изменяется значение радиусов-векторов начала и конца линии, но они остаются равными.
Отсюда может быть сделан вывод, что изменение перепада напряжений влияет на положение центра круговой диаграммы только начала линии и не влияет на положение центра диаграммы конца линии. Кроме того, изменение перепада напряжений влияет и на значение радиуса-вектора круговых диаграмм начала и конца линии и, следовательно, на ее пропускную способность.
Следует отметить, что обе диаграммы при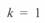 
пересекаются с осью абсцисс в одной точке при 
; при этом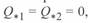 
, что соответствует передаче натуральной мощности.
Рассмотрим изменение круговых диаграмм при увеличении длины линии от нуля до 3000 км. Параметры обеих круговых диаграмм — значения радиусов-векторов и положение их центров — зависят от длины линии. При ее нулевой длине (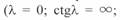 
; 
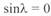) положение центров смещается в бесконечность, соответственно значение радиусов-векторов также равно бесконечности. Поэтому обе диаграммы вырождаются в прямые, которые совпадают с осью абсцисс (рис. 3. 9, а).
По мере увеличения длины линии центры круговых диаграмм смещаются в направлении центра координат, а значение радиусов- векторов уменьшается, что свидетельствует о снижении пропускной способности линии (рис. 3. 9, б).
При длине линии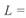 
= 1500 км (четвертьволновая линия, 
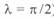) центры обеих диаграмм совпадают с началом координат, значение радиусов-векторов определяется значением перепада напряжений 
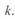. При 
и 
обе диаграммы пересекают ось абсцисс при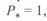 
, что подтверждает сделанный ранее вывод о том, что при данной длине 
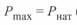(рис. 3. 9, в).
|
|
|
При дальнейшем увеличении длины линии 1500 <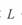 
< 3000 км центры круговых диаграмм продолжают смещаться в том же направлении, так как в этом диапазоне длин 
. При этом диаграммы начала и конца линии меняются местами: центр диаграммы начала линии переходит в отрицательную полуплоскость, центр диаграммы конца — в положительную. Важно отметить, что положение рабочих зон каждой из диаграмм на окружности не меняется, поскольку в указанном диапазоне длин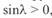 
, и знак второго члена уравнений круговых диаграмм (3. 57), (3. 59) тоже не меняется. Это приводит к тому, что режим линии резко меняется по сравнению с режимом линий, длина которых меньше 1500 км.
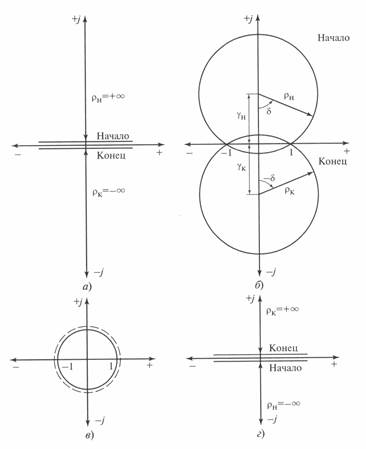
Рис. 3. 9. Круговые диаграммы линии при изменении ее длины от нуля до 3000 км:
Когда длина линии достигает 3000 км, центры обеих диаграмм смещаются в бесконечность (начало линии — в минус бесконечность, конец линии — в плюс бесконечность). Радиусы-векторы обеих окружностей также равны бесконечности, а сами окружности вырождаются в прямые, которые совпадают с осью абсцисс (рис. 3. 9, г). Это говорит о том, что пропускная способность линии длиной 3000 км равна пропускной способности линии нулевой длины, т. е. теоретически также равна бесконечности.
Более подробно режимы линий длиной свыше 1500 км рассматриваются ниже.
|
|
|
