Средние величины и показатели вариации

СРЕДНИЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ВАРИАЦИИ

1. Сущность и значение средних величин

2. Виды средних величин

3. Показатели вариации

 

1. Целый ряд признаков, присущих отдельным объектам, в статистике различаются по величине. Однако, при всем разнообразии размеров признака у отдельных объектов совокупности, существуют характерные для совокупности в целом размеры этих признаков, которые выражаются в статистике при помощи средней величины.

    Средняя величина – обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени. Он выражает величину признака, отнесенную к единице совокупности. Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.

Отличительной особенностью средних является то, что в них погашаются индивидуальные различия признака у отдельных единиц совокупности, в результате чего появляется возможность охарактеризовать общие черты и свойства массовых экономических явлений. Вместе с тем, средние показатели иногда приводят к необъективным выводам при проведении экономико-статистического анализа, так как они игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.

2. Средние величины делятся на два больших класса:

- степенные средние

- структурные средние.

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя считается по несгруппированным данным, а взвешенная средняя считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения.

Виды степенных средних

Вид степенной средней	Показатель степени	Формула расчета
		простая	взвешенная
Гармоническая	-1
Геометрическая	®0
Арифметическая
Квадратическая
Кубическая

Средняя арифметическая простая применяется, когда количество вариантов по конкретному признаку встречается по одному или одинаковому числу раз.

Пример. Имеются следующие данные о з/п рабочих участка за сентябрь.

Профессия	Количество рабочих, чел.	З/п каждого рабочего, д. е.
Токарь		1700, 1208, 917, 1620, 1400
Фрезеровщик		1810, 1550
Слесарь		1210, 1380, 870

Вычислить среднюю з/п рабочих участка за сентябрь.

 

Средняя арифметическая взвешенная применяется при условии повторения признака неодинаковое число раз.

Пример. Имеется распределение рабочих участка по величине месячной з/п.

Месячная з/п, д. е. (х)	2, 5	7, 5	12, 5	17, 5
Число рабочих, чел (f)

Рассчитать среднюю месячную з/п.

 

Средняя гармоническая – величина, обратная средней арифметической. Средняя гармоническая простая рассчитывается в том случае, если имеются одинаковые объекты, различные по какому-либо признаку.

Пример. Два автомобиля разных марок работают на одной марке бензина. Первый автомобиль имеет удельных расход 0, 05 л/км, второй – 0, 08 л/км.

Определить средний удельный расход бензина по двум автомобилям.

 

Средняя гармоническая взвешенная рассчитывается в случае, если по условию дано произведение признака на частоту (xf).

Пример. Определить среднюю продолжительность рабочего дня на предприятии по данным таблицы.

№ цеха	Средняя фактическая продолжительность рабочего дня, час (х)	Отработанное время, чел*час (xf)
	7, 8
	7, 2

 

Средняя геометрическая применяется, когда индивидуальное значение признака представляет собой относительную величину динамики (средний коэффициент роста).

Пример. Рассчитать среднегодовой темп роста объема продукции за период с 2003 по 2005 год.

Годы	Производство продукции, тыс. руб.	Темпы роста
		400/370=1, 081
		420/400=1, 05

 

Средняя квадратическая применяется для расчета среднего квадратического отклонения, являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).

Пример. Подача жидкого топлива для технологического процесса осуществляется в цехе тремя трубопроводами с диаметром 2, 5 и 6 см. При капитальном ремонте здания цеха эти трубопроводы будут заменены на три новых одинакового диаметра при сохранении их общей пропускной способности.

Определить средний диаметр трубы (диаметр новой трубы).

 

Величины степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака при различных значениях степени не одинаковы. Чем выше степень средней, тем больше величина самой средней (правило мажорантности средних):

Структурные средние

Мода – числовое значение признака, которое наиболее часто встречается в ряду распределения. Может определяться по несгруппированным данным, а также для дискретного и интервального ряда.

Расчет моды по несгруппированным данным

Пример 8. Известно, что 7 сотрудников отдела кадров имеют следующий стаж работы, лет: 5 2 4 3 4 2 2.

Так как чаще всего встречается стаж работы 2 года, он является модальным.

Расчет моды по дискретному ряду распределения

Особенности применения моды для дискретного ряда:

1. если все значения вариационного ряда имеют одинаковую частоту, то этот вариационный ряд не имеет моды;

2. если два соседних варианта имеют одинаковую наибольшую частоту, то мода вычисляется как среднее арифметическое из этих вариантов;

3. если два несоседних варианта имеют одинаковую наибольшую частоту, то вариационный ряд называется бимодальным;

4. если таких вариантов более двух, то ряд полимодальный.

Пример 9. Имеется ряд распределения рабочих по выработке деталей.

Выработка деталей за смену, шт. (х)	Число рабочих, чел. (f)	Сумма накопленных частот
		2+4=6
		6+5=11
		11+3=14
		14+1=15
Итого

Поскольку наибольшее число рабочих (5 чел. ) имеют выработку 20 деталей, мода равна 20.

Расчет моды по интервальному ряду распределения

Для интервальных рядов распределения мода рассчитывается по формуле:

где х₀ - нижняя граница модального интервала;

i - величина модального интервала;

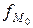- частота модального интервала;

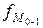- частота интервала, предшествующего модальному;

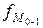-частота интервала, следующего за модальным.

Пример 10. Имеются предприятия региона, распределенные на группы по стоимости опф. Определить моду.

Группы опф, млн. руб. (х)	Число обследованных предприятий (f)	Сумма накопленных частот
14-16
16-18		2+6=8
18-20		8+10=18
20-22		18+4=22
22-24		22+3=25
Итого

Решение.

Модальный интервал -18-20, так как для него характерна наибольшая частота (число обследованных предприятий).

Мо=18+2(10-6)/((10-6)+(10-4))=18, 8 млн. руб. (всегда лежит в модальном интервале).

Вывод: предприятия, имеющие величину опф в размере 18, 8 млн. руб. представляют собой наибольшую группу в общем объеме рассматриваемых предприятий.

На практике мода иногда используется вместо средней арифметической или вместе с ней, например, при определении наиболее ходовых размеров одежды и обуви, что учитывается при планировании их производства.

Медиана – величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Рассчитывается по несгруппированным данным, а также для дискретного и интервального ряда.

Расчет медианы по несгруппированным данным

Вначале для определения медианы необходимо провести ранжирование.

Если ряд состоит из нечетного количества вариантов, место медианы определяется по формуле: Nме=(n+1)/2, где n – количество единиц совокупности.

Для четного ряда медиана рассчитывается как средняя арифметическая простая из двух значений, находящихся в середине ряда.

Пример 11. По условию примера 8 найти медиану.

Решение.

Проведем ранжирование исходных данных: 2 2 2 3 4 4 5.

Ряд нечетный, поэтому место медианы (7+1)/2=4, т. е. медианный стаж – 3 года (половина работников имеют стаж менее 3-х лет, половина – более 3-х лет).

Расчет медианы по дискретному и интервальному ряду распределения

Алгоритм нахождения медианы для дискретного ряда (медианного интервала для интервального ряда):

1. определяем общую сумму и полусумму частот;

2. для каждого значения признака (интервала) определяем сумму накопленных частот.

3. Медианным будет то значение признака (тот интервал), для которого сумма накопленных частот впервые превысит их полусумму.

Для интервального ряда медиана рассчитывается по формуле:

где х₀ - нижняя граница медианного интервала;

i – величина медианного интервала;

         - сумма частот;

         - сумма частот, накопленная до начала медианного    интервала;

 - частота медианного интервала.

Пример 12. По данным примера 9 найти медиану.

Решение.

Определяем сумму накопленных частот: 15

Определяем полусумму накопленных частот: 15/2=7, 5.

Медианным является то значение признака, для которого сумма накопленных частот впервые превысит полусумму (11> 7, 5). Т. о., медиана – 20 деталей, т. е. половина рабочих имеют выработку более 20 деталей, половина - менее 20 деталей.

Пример 13. По данным примера 10 найти медиану.

Решение.

Определяем сумму накопленных частот: 25.

Определяем полусумму накопленных частот: 25/2=12, 5.

Медиана находится в том интервале, в котором сумма накопленных частот впервые превысит полусумму (18> 12, 5).

Применяем формулу: Ме=18+2(12, 5-8)/10=18, 9 млн. руб. (всегда лежит в медианном интервале).

Вывод: половина предприятий имеют стоимость опф менее 18, 9 млн. руб., остальные – более 18, 9 млн. руб.

Медиана используется при изучении распределения семей по величине дохода, при проектировании оптимального положения остановок общественного транспорта, складских помещений и т. д.

Мода и медиана имеют преимущество перед средней арифметической для ряда распределения с открытыми интервалами.

3. Для исследования колеблемости средней величины в статистике возникает необходимость изучения признаков вариации и ее измерения.

Вариация – несовпадение уровней одного и того же показателя у разных объектов.

Вариацией называется изменчивость только тех явлений, на которые воздействуют внешние факторы и причины. Тогда как о явлениях, изменяющихся в силу своей внутренней природы, нельзя говорить, что они подвержены вариации. Например, рост человека, меняющийся в течение жизни. Изучение изменчивости роста отдельного человека, который, допустим, к году составляет 0, 8 м, а к 25 годам – 1, 79 см путем расчета среднего роста будет некорректным, так как в начале жизни рост был небольшой в силу естественных причин.

Не следует путать с вариацией изменение размера признака у одной и той же единицы совокупности, наблюдаемой в разные моменты или периоды времени. Такое изменение называется изменением во времени или динамикой явления и исследуется с помощью специальных методов.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: