 |
Оглавление. Введение. 1. Параметрическая оптимизация системы управления с использованием метода наискорейшего спуска. 1. 1. Содержание
|
|
|
|
ОГЛАВЛЕНИЕ
Стр.
ВВЕДЕНИЕ. . 4
1. ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ СИСТЕМЫ УПРАВЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ МЕТОДА НАИСКОРЕЙШЕГО СПУСКА. . 3
1. 1. Содержание. 3
1. 2. Рекомендации по выполнению. . 8
1. 3. Требования к отчёту. 21
1. 4. Контрольные вопросы. . 22
2. ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ СИТЕМЫ УПРАВЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ ортогонального композиционного планирования (ОКП) 23
2. 1. Содержание. 23
2. 2. Рекомендации по выполнению. . 25
2. 3. Требования к отчёту. 29
2. 4. Контрольные вопросы. . 29
3. ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ СИСТЕМЫ УПРАВЛЕНИЯ С ПРИМЕНЕНИЕМ МЕТОДА ДЕФОРМИРОВАННОГО МНОГОГРАННИКА. . 30
3. 1. Содержание. 30
3. 2. Рекомендации по выполнению. . 31
3. 3. Требования к отчёту. 36
3. 4. Контрольные вопросы. . 36
4. АЛГОРИТМ ПРОГРАММЫ QUICK_DESCENT ДЛЯ ПОИСКА МИНИМУМА ФУНКЦИОНАЛА ПО МЕТОДУ НАИСКОРЕЙШЕГО СПУСКА. . 37
4. 1. Основной алгоритм. . 37
4. 2. Подпрограмма “Конструирование матрицы планирования”. 38
4. 3. Подпрограмма “Вычисление значения функционала в каждой точке плана”. 39
4. 4. Подпрограмма “Вычисление коэффициентов bj, j=0, 1... k”. 40
4. 5. Подпрограмма “Поиск базового параметра”. 41
4. 6. Подпрограмма “Вычисление шагов движения для каждого параметра”. 42
4. 7. Подпрограмма “Определение наименьшего значения функционала на текущем цикле” 42
ЗАКЛЮЧЕНИЕ. . 44
ЛИТЕРАТУРА. . 45
ПРИЛОЖЕНИЕ. Варианты заданий к работам. . 46
ВВЕДЕНИЕ
Методические указания посвящены работам по параметрической оптимизации систем управления с применением современных алгоритмов поиска экстремума функции нескольких переменных. Каждая работа включает в себя следующие разделы: цель работы, содержание, рекомендации по выполнению, требования к отчету и контрольные вопросы.
|
|
|
Рассматриваются следующие методы поиска экстремума функции нескольких переменных:
· метод наискорейшего спуска;
· метод, основанный на ортогональном композиционном планировании;
· метод деформированного многогранника, разработанный Нелдером и Мидом.
Каждому методу посвящена отдельная работа. В первых двух работах подробно изучаются алгоритмы поиска экстремума по методу наискорейшего спуска и методу, основанному на ортогональном композиционном планировании, применительно к задаче параметрической оптимизации системы управления. В последней работе решается только задача параметрической оптимизации без детального рассмотрения упомянутого метода деформированного многогранника.
Все работы выполняются с использованием математического пакета MatLab. В ходе проведения работ используются специальные программные средства, написанные средствами встроенного языка программирования MatLab. Целью данных программных средств является исключение сложных ручных расчетов и наглядное представление результатов.
1. ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ СИСТЕМЫ УПРАВЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ МЕТОДА НАИСКОРЕЙШЕГО СПУСКА
Цель работы: приобретение практических навыков по расчёту параметров регуляторов, обеспечивающих наперёд заданные динамические характеристики системы, с применением методов планирования эксперимента.
1. 1. Содержание
Рассматривается система управления объектом, структурная схема которой представлена на рис. 1. 1.
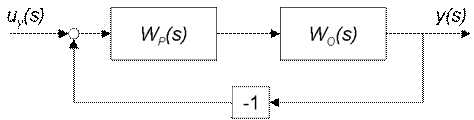
Рис. 1. 1
На рис. 1. 1 обозначено:  ,
,  - передаточные функции объекта и регулятора соответственно;
- передаточные функции объекта и регулятора соответственно;  - входная переменная;
- входная переменная;  - выходная переменная.
- выходная переменная.
Требуется путём изменения параметров регулятора обеспечить проектируемой системе такую реакцию на ступенчатое управляющее воздействие, которая совпадает с аналогичной, заданной эталонной моделью. В качестве эталонной, в зависимости от варианта, принимается модель, соответствующая стандартной форме Баттерворта или бинома Ньютона n-ого порядка. Рассматриваемые стандартные формы имеют вид:
|
|
|
a) форма Баттерворта:
 , при n=2
, при n=2
 , при n=3
, при n=3
 , при n=4
, при n=4
b) форма бинома Ньютона:
 , при n=2
, при n=2
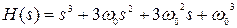 , при n=3
, при n=3
 , при n=4,
, при n=4,
где 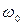 - параметр, характеризующий быстродействие.
- параметр, характеризующий быстродействие.
В качестве функционала качества предлагается принять интегральный квадратичный критерий, для которого квадратичная форма формируется, как квадрат разности между эталонным движением и движением выходной переменной модели проектируемой системы при отработке обеими моделями заданного управляющего воздействия.
Общее математическое описание, соответствующее сформулированной задаче, представлено в виде структурной схемы на рис. 1. 2, где 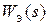 ,
,  - передаточная функция и выходная переменная эталонной модели соответственно.
- передаточная функция и выходная переменная эталонной модели соответственно.
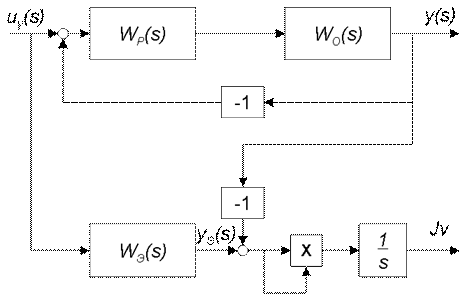
Рис. 1. 2
Исходя из данной структурной схемы, критерий качества может быть записан как:
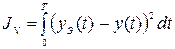 ,
,
где t – время, независимая переменная; Т – период, в течение которого производится расчёт функционала.
Таким образом, задачей работы является определение таких значений параметров регуляторов, при которых JV будет минимальным. Так как аналитическая зависимость
 ,
,
где  ,
,  - функция отклика и параметры регулятора соответственно, неизвестна, необходимо применять специальные методы поиска минимума функции
- функция отклика и параметры регулятора соответственно, неизвестна, необходимо применять специальные методы поиска минимума функции  . Среди таковых в данной работе рекомендуется использовать метод наискорейшего спуска. Логика организации эксперимента с использованием этого метода заключается в следующем. Сначала выбирается некая область в пространстве независимых переменных, где ставится эксперимент, по результатам которого делается линейное приближение этой локальной окрестности поверхности отклика. Далее осуществляется движение по поверхности отклика в направлении градиента линейного приближения. Если необходимо, делается ещё одно линейное приближение, и так продолжается до тех пор, пока линейное приближение поверхности отклика оказывается непригодным. Далее минимизация функционала осуществляется на основе построения квадратичной модели поверхности отклика.
. Среди таковых в данной работе рекомендуется использовать метод наискорейшего спуска. Логика организации эксперимента с использованием этого метода заключается в следующем. Сначала выбирается некая область в пространстве независимых переменных, где ставится эксперимент, по результатам которого делается линейное приближение этой локальной окрестности поверхности отклика. Далее осуществляется движение по поверхности отклика в направлении градиента линейного приближения. Если необходимо, делается ещё одно линейное приближение, и так продолжается до тех пор, пока линейное приближение поверхности отклика оказывается непригодным. Далее минимизация функционала осуществляется на основе построения квадратичной модели поверхности отклика.
|
|
|
Эксперимент, на основе которого делается линейное приближение, ставится по плану. План эксперимента образуется путём варьирования каждого из факторов (параметров регулятора) на нескольких уровнях относительно базовой точки, представляющей центр эксперимента. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Результатом эксперимента является некоторое приближение функции  в окрестности выбранной базовой точки -
в окрестности выбранной базовой точки -  (отрезок ряда Тейлора). Если
(отрезок ряда Тейлора). Если  включает только линейные члены полинома и их произведения, то для оценки её параметров используется план эксперимента с варьированием всех факторов на двух уровнях. Такой план называется планом 2k, где 2k = N – число всех возможных опытов, k – количество варьируемых факторов. Геометрическая интерпретация функции отклика
включает только линейные члены полинома и их произведения, то для оценки её параметров используется план эксперимента с варьированием всех факторов на двух уровнях. Такой план называется планом 2k, где 2k = N – число всех возможных опытов, k – количество варьируемых факторов. Геометрическая интерпретация функции отклика  , функции
, функции  и плана эксперимента для двух факторов показана на рис. 1. 3.
и плана эксперимента для двух факторов показана на рис. 1. 3.

Рис. 2. 3
На рисунке обозначено: X1 и X2 – варьируемые параметры (натуральные значения); X1 min, X1 max, X2 min, X2 max – предельные значения варьируемых параметров;  - базовая точка; Δ X1, Δ X2, +1, -1 – интервалы варьирования факторов в натуральных и кодированных значениях соответственно; x1, x2 – кодированные значения варьируемых параметров. Связь между кодированными и натуральными значениями факторов имеет вид:
- базовая точка; Δ X1, Δ X2, +1, -1 – интервалы варьирования факторов в натуральных и кодированных значениях соответственно; x1, x2 – кодированные значения варьируемых параметров. Связь между кодированными и натуральными значениями факторов имеет вид:

Рассмотрим теперь подробнее практический аспект метода наискорейшего спуска. Процедура поиска по этому методу как правило выполняется в несколько циклов. Последовательность проведения каждого цикла такова:
1. С центром в исходной точке 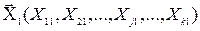 , где
, где  - принятые как за исходные значения варьируемых параметров, проводится полный факторный эксперимент 2k в соответствии с матрицей планирования, показанной в табл. 1. 1.
- принятые как за исходные значения варьируемых параметров, проводится полный факторный эксперимент 2k в соответствии с матрицей планирования, показанной в табл. 1. 1.
|
|
|
Таблица 1. 1
|
Номер опыта |
Матрица планирования |
Значение Jv | ||||
| x0 | x1 | x2 | … | xk | ||
| +1 | -1 | -1 | … | -1 | Jv1 | |
| +1 | +1 | -1 | … | -1 | Jv2 | |
| +1 | -1 | +1 | … | -1 | Jv3 | |
| +1 | +1 | +1 | … | -1 | Jv4 | |
| +1 | -1 | -1 | … | -1 | Jv5 | |
| … | … | … | … | … | … | … |
| N | +1 | +1 | +1 | … | +1 | JvN |
Принцип построения матрицы планирования следующий: первая строка выбирается так, чтобы все изучаемые факторы находились на нижних уровнях (-1); следующие строки плана образуются так, чтобы при построчном переборе всех вариантов частота смены знака варьируемых параметров для каждого последующего параметра была вдвое меньше, чем предыдущего.
Линейное приближение исследуемой функции в окрестности исходной точки  строится на основе полученных из эксперимента значений Jvj, j=1, 2, 3…, N:
строится на основе полученных из эксперимента значений Jvj, j=1, 2, 3…, N:
 ,
,
где xj, j=1, 2, …, k – кодированные значения варьируемых параметров; bj, j=0, 1, …, k – коэффициенты полиномиальной модели, определяемые как:
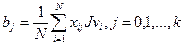 .
.
Следует учитывать, что движение по градиенту будет эффективным, если значения коэффициентов bj примерно одного порядка.
2. Координаты точек, то есть значения варьируемых параметров, в направлении градиента рассчитываются последовательным прибавлением к основным уровням Xj1 величин, равных шагам движения λ j. Параметр, создающий максимальное приращение в направлении градиента, принимается за базовый, то есть max(bjΔ Xj)= bбΔ Xб. Для базовой переменной выбирается базовый шаг движения λ б ≈ 0. 5Δ Xб. Размер и знак шагов движения λ j для всех параметров вычисляются по формуле:
 ,
,  ,
, 
3. С выбранными размерами и знаками шагов рассчитываются координаты точек  факторного пространства. j – я координата h – й точки траектории равна:
факторного пространства. j – я координата h – й точки траектории равна:
 ,
,  ,
, 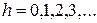
4. Значения варьируемых параметров на каждом шаге движения в направлении градиента исследуемой функции (координаты точек  на траектории, h – порядковый номер шага) реализуются в системе для экспериментальной оценки соответствующих им значений JV. Закончить движение в направлении градиента следует при прекращении уменьшения значений JV. Координаты точки
на траектории, h – порядковый номер шага) реализуются в системе для экспериментальной оценки соответствующих им значений JV. Закончить движение в направлении градиента следует при прекращении уменьшения значений JV. Координаты точки  с наименьшим значением JV принимаются за новые нулевые уровни варьируемых параметров.
с наименьшим значением JV принимаются за новые нулевые уровни варьируемых параметров.
Цикл наискорейшего спуска повторяется до тех пор, пока поиск минимума функционала качества по этому методу становится неэффективным.
|
|
|


