 |
1. 3. Требования к отчёту. 1. 4. Контрольные вопросы. 2. Параметрическая оптимизация ситемы управления с использованием ортогонального композиционного планирования (ОКП)
|
|
|
|
1. 3. Требования к отчёту
В отчёте следует привести: цель работы; описание задачи и этапов её решения; структурную схему системы и её подсистем; текст программы quick_descent в части изменений, сделанных в ней; матрицу планирования эксперимента; результаты машинных вычислений; таблицы исходных данных и движения по градиенту; необходимые графики; выводы.
1. 4. Контрольные вопросы
1. Объясните необходимость использования специальных методов для поиска экстремума исследуемой в работе функции?
2. В чём заключается смысл метода наискорейшего спуска?
3. Какие программные средства могут быть использованы для решения задачи расчёта параметров регулятора, отвечающих наперёд заданным динамическим характеристикам системы?
4. Какие исходные данные необходимы для запуска процедуры поиска минимума функции по методу наискорейшего спуска?
5. Из каких соображений могут быть выбраны интервалы варьирования параметров?
6. Объясните принцип построения матрицы планирования эксперимента при ПФЭ?
7. Опишите последовательность действий при поиске минимума функции по методу наискорейшего спуска в пределах одного цикла.
8. Когда следует прекратить решение задачи по методу наискорейшего спуска?
2. ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ СИТЕМЫ УПРАВЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ ортогонального композиционного планирования (ОКП)
Цель работы: приобретение практических навыков решения задач параметрической оптимизации с использованием ортогонального композиционного планирования.
2. 1. Содержание
Описание локальной области поверхности отклика, имеющей существенную кривизну, где поиск минимума методом наискорейшего спуска является неэффективным, может быть получено в виде полиномиальной модели второго порядка:
|
|
|
, (2. 1)
где 
– коэффициенты полиномиальной модели второго порядка, j, u=1, 2, …, k, j< u. Для определения значений этих коэффициентов рекомендуется использовать ортогональный центральный композиционный план второго порядка, который образуется путём добавления к “ядру”, состоящему из плана 2k, точки в центре плана и 2k так называемых “звёздных” точек. Матрица планирования применительно к данному случаю приведена в табл. 2. 1.
Таблица 2. 1
|
Точки плана |
Номер опыта |
Матрица планирования |
Значение Jv | ||||||||||
| z0 | z1 | z2 | … | zq | … | zn-1 | |||||||
| x0 | x1 | x2 | … | xk | x1 x2 | … | xk-1 xk | x12-λ | … | xk2-λ | |||
|
Ядро плана | +1 | -1 | -1 | … | -1 | +1 | … | +1 | 1-λ | … | 1-λ | Jv1 | |
| +1 | +1 | -1 | -1 | -1 | +1 | 1-λ | 1-λ | Jv2 | |||||
| +1 | -1 | +1 | -1 | -1 | +1 | 1-λ | 1-λ | Jv3 | |||||
| +1 | +1 | +1 | -1 | +1 | +1 | 1-λ | 1-λ | … | |||||
| +1 | -1 | -1 | -1 | +1 | +1 | 1-λ | 1-λ | ||||||
| … | … | … | … | … | … | … | … | … | |||||
| 2k | +1 | +1 | +1 | +1 | +1 | +1 | 1-λ | 1-λ | |||||
|
Звёздные точки | 2k+1 | +1 | + γ | … | … | γ 2-λ | … | -λ | |||||
| 2k+2 | +1 | - γ | γ 2-λ | -λ | |||||||||
| 2k+3 | +1 | + γ | -λ | -λ | |||||||||
| 2k+4 | +1 | - γ | -λ | -λ | |||||||||
| … | … | … | … | … | … | … | … | … | |||||
| 2k+2k-1 | +1 | + γ | -λ | γ 2-λ | |||||||||
| 2k+2k | +1 | - γ | -λ | γ 2-λ | |||||||||
| Центр плана | 2k+2k+1 | +1 | … | … | -λ | … | -λ | JvN | |||||
В таблице 2. 1 приняты следующие обозначения: x0, x1, …, xk – варьируемые параметры; zq – обозначение функции в q – м столбце; N – общее число точек плана; γ, 
– параметры, зависящие от числа варьируемых параметров. Значения параметров γ, для k=2, 3, 4 приведены в табл. 2. 2.
|
|
|
Таблица 2. 2
| k | N | γ | λ |
| 1, 0 | 0, 6667 | ||
| 1, 215 | 0, 73 | ||
| 1, 414 | 0, 8 |
С учётом обозначений, приведённых в табл. 2. 1, можно перейти к линейной записи полинома (2. 1):
,
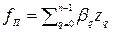где 
- общее число коэффициентов полинома 2-ого порядка;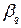 
- коэффициент при функции независимых переменных, указанной в q-м столбце матрицы планирования:
, q=0, 1, 2, …, (n-1). (2. 2)
Для 
из (2. 1) в соответствии с (2. 2) имеем:
. (2. 3)
Таким образом, полином второго порядка (2. 1) с рассчитанными по формулам (2. 2) и (2. 3) коэффициентами может быть использован для предсказания точки минимума исследуемой функции в локальной области эксперимента. Для этого приравнивают к нулю частные производные функции по каждой координате, получая при этом систему k-уравнений:
, j=1, 2, …, k. (2. 4)
Решая систему линейных уравнений (2. 4), получим координаты точки минимума в кодированных значениях (начало координат в центре эксперимента).
|
|
|
