 |
2. 3. Требования к отчёту. 2. 4. Контрольные вопросы. 3. Параметрическая оптимизация системы управления с применением метода деформированного многогранника
|
|
|
|
2. 3. Требования к отчёту
В отчёте следует привести: цель работы; описание задачи и этапов её решения; таблицу исходных данных; матрицу планирования эксперимента; расчёт коэффициентов полиномиальной модели; расчёт параметров регулятора; необходимые графики; выводы.
2. 4. Контрольные вопросы
1. В каком случае необходимо применять для поиска экстремума функции ОКП?
2. Какие элементы включает в себя матрица планирования эксперимента в случае ОКП?
3. Каким образом выбираются исходные данные для решения задачи минимизации функционала качества по рассматриваемому методу?
4. Опишите последовательность действий при поиске экстремума функции с использованием ОКП.
3. ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ СИСТЕМЫ УПРАВЛЕНИЯ С ПРИМЕНЕНИЕМ МЕТОДА ДЕФОРМИРОВАННОГО МНОГОГРАННИКА
Цель работы: получение практических навыков по решению задач параметрической оптимизации с применением стандартной функции поиска экстремума функции из раздела Optimization Toolbox пакета MatLab, использующей алгоритм деформированного многогранника.
3. 1. Содержание
Рассматривается система управления объектом, структурная схема которой приведена на рис. 1. 1.
Ставится задача определения параметров регулятора, при которых одновременно выполняются два условия:
1) реакция выходной переменной на ступенчатое управляющее воздействие должна совпадать с аналогичной, заданной эталонной моделью;
2) система должна иметь как можно большее быстродействие, которое задаётся быстродействием эталонной модели.
В качестве эталонных моделей предлагаются следующие:
· соответствующая настройке на симметричный оптимум (СО):
,
где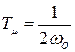 
- параметр, характеризующий быстродействие эталонной модели;
|
|
|
· соответствующие стандартным формам Баттерворта (рассмотрены ранее);
· соответствующие стандартным формам бинома Ньютона (рассмотрены ранее).
Вид эталонной модели определяется заданием. Решение задачи рекомендуется начинать с варианта, для которого быстродействие эталонной модели равно значению, вычисленному из выражения 
, аналогично тому, как это делалось во второй работе. При успешном решении задачи для данного быстродействия эталонной модели его следует увеличить вдвое, после чего повторить выполнение всего объёма работ по оптимизации. Аналогичным образом поступают до тех пор, пока не перестанет выполняться первое условие поставленной задачи. Если следовать вышеизложенным рекомендациям, то последнее значение быстродействия 
будет отличаться от предпоследнего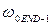 
в два раза. Далее можно попытаться найти некоторое промежуточное значение быстродействия между 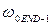и , при котором ещё выполняется первое условие поставленной задачи. Если такое значение быстродействия будет найдено, то задача считается решенной. В этом случае следует зафиксировать значениями параметров регулятора и значение функционала качества.
Для оценки степени приближения движения реальной выходной переменной к эталону рекомендуется применять интегральный квадратичный критерий, как и в предыдущих работах.
В качестве метода минимизации функционала качества 
в данной работе применяется модифицированный метод симплексного планирования, разработанный Нелдером и Мидом.
|
|
|
