 |
2.2. Рекомендации по выполнению
|
|
|
|
2. 2. Рекомендации по выполнению
Поиск минимума функции с использованием ОКП следует начинать, как и в методе наискорейшего спуска, с определения начальной (базовой) точки эксперимента и интервалов варьирования переменных относительно неё. В качестве базовых могут быть взяты координаты точки, полученные в последнем цикле при решении задачи минимизации по методу наискорейшего спуска в предыдущей работе. Интервалы варьирования параметров выбираются в соответствии с ранее изложенными указаниями.
Для рассматриваемой системы исходные данные применительно к методу звёздных точек представлены в табл. 2. 3.
Таблица 2. 3
| Варьируемая переменная |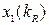 
| 
| 
|
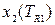
| Основной уровень | 0. 0326 | 0. 0685 | |
| Интервал варьирования | 0. 00081 | 0. 0003 | 0. 3 |
| Верхний уровень (+1) | 0. 0334 | 0. 0688 | 7. 3 |
| Нижний уровень (-1) | 0. 0318 | 0. 0682 | 6. 7 |
| Уровень + γ (+1. 215) | 0. 0336 | 0. 0689 | 7. 36 |
| Уровень – γ (-1. 215) | 0. 0316 | 0. 0681 | 6. 64 |
После определения исходных данных требуется построить матрицу планирования для конкретного числа переменных. В частном случае для рассматриваемых трёх параметров (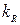 
, 
, 
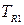) матрица планирования представлена в табл. 2. 4.
Таблица 2. 4
|
Точки плана |
Номер опыта |
Матрица планирования |
Значение Jv | |||||||||||
| z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 | |||||
| x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x12-l | x22-l | x32-l | |||||
|
Ядро плана | +1 | -1 | -1 | -1 | +1 | +1 | +1 | 0, 27 | 0, 27 | 0, 27 | 0, 023286 | |||
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | 0, 27 | 0, 27 | 0, 27 | 0, 023702 | ||||
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | 0, 27 | 0, 27 | 0, 27 | 0, 023375 | ||||
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | 0, 27 | 0, 27 | 0, 27 | 0, 02364 | ||||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | 0, 27 | 0, 27 | 0, 27 | 0, 022241 | ||||
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | 0, 27 | 0, 27 | 0, 27 | 0, 022675 | ||||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | 0, 27 | 0, 27 | 0, 27 | 0, 02233 | ||||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | 0, 27 | 0, 27 | 0, 27 | 0, 022612 | ||||
|
Звёздные
точки | +1 | +1, 215 | 0, 74623 | -0, 73 | -0, 73 | 0, 02322 | ||||||||
| +1 | -1, 215 | 0, 74623 | -0, 73 | -0, 73 | 0, 0228 | |||||||||
| +1 | +1, 215 | -0, 73 | 0, 74623 | -0, 73 | 0, 02286 | |||||||||
| +1 | -1, 215 | -0, 73 | 0, 74623 | -0, 73 | 0, 02285 | |||||||||
| +1 | +1, 215 | -0, 73 | -0, 73 | 0, 74623 | 0, 02225 | |||||||||
| +1 | -1, 215 | -0, 73 | -0, 73 | 0, 74623 | 0, 02351 | |||||||||
| Центр плана | +1 | -0, 73 | -0, 73 | -0, 73 | 0, 02285 | |||||||||
Значение функционала качества в какой-либо точке плана вычисляется в MatLab путём подстановки в модель Simulink значений параметров регулятора, соответствующих данной точке. Полученные таким образом значения функционала качества (см. столбец “Значение Jv” в табл. 2. 4) используются для расчёта коэффициентов полиномиальной модели второго порядка (2. 1). Так как для определения коэффициентов используется формула_(2. 2), то целесообразно сначала вычислить следующие значения:
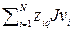и 
, где q=0, 1, 2, …, (n-1).
В табл. 2. 5 и табл. 2. 6 приведён такой расчёт для рассматриваемого примера.
Таблица 2. 5
| № опыта | z0Jv | z1Jv | z2Jv | z3Jv | z4Jv | z5Jv | z6Jv | z7Jv | z8Jv | z9Jv |
| 0, 023286 | -0, 02329 | -0, 02329 | -0, 02329 | 0, 023286 | 0, 023286 | 0, 023286 | 0, 006287 | 0, 006287 | 0, 006287 | |
| 0, 023702 | 0, 023702 | -0, 0237 | -0, 0237 | -0, 0237 | -0, 0237 | 0, 023702 | 0, 0064 | 0, 0064 | 0, 0064 | |
| 0, 023375 | -0, 02338 | 0, 023375 | -0, 02338 | -0, 02338 | 0, 023375 | -0, 02338 | 0, 006311 | 0, 006311 | 0, 006311 | |
| 0, 02364 | 0, 02364 | 0, 02364 | -0, 02364 | 0, 02364 | -0, 02364 | -0, 02364 | 0, 006383 | 0, 006383 | 0, 006383 | |
| 0, 022241 | -0, 02224 | -0, 02224 | 0, 022241 | 0, 022241 | -0, 02224 | -0, 02224 | 0, 006005 | 0, 006005 | 0, 006005 | |
| 0, 022675 | 0, 022675 | -0, 02268 | 0, 022675 | -0, 02268 | 0, 022675 | -0, 02268 | 0, 006122 | 0, 006122 | 0, 006122 | |
| 0, 02233 | -0, 02233 | 0, 02233 | 0, 02233 | -0, 02233 | -0, 02233 | 0, 02233 | 0, 006029 | 0, 006029 | 0, 006029 | |
| 0, 022612 | 0, 022612 | 0, 022612 | 0, 022612 | 0, 022612 | 0, 022612 | 0, 022612 | 0, 006105 | 0, 006105 | 0, 006105 | |
| 0, 02322 | 0, 028212 | 0, 017327 | -0, 01695 | -0, 01695 | ||||||
| 0, 0228 | -0, 0277 | 0, 017014 | -0, 01664 | -0, 01664 | ||||||
| 0, 02286 | 0, 027775 | -0, 01669 | 0, 017059 | -0, 01669 | ||||||
| 0, 02285 | -0, 02776 | -0, 01668 | 0, 017051 | -0, 01668 | ||||||
| 0, 02225 | 0, 027034 | -0, 01624 | -0, 01624 | 0, 016604 | ||||||
| 0, 02351 | -0, 02856 | -0, 01716 | -0, 01716 | 0, 017544 | ||||||
| 0, 02285 | -0, 01668 | -0, 01668 | -0, 01668 | |||||||
| Сумма | 0, 344201 | 0, 001907 | 6, 51E-05 | -0, 00568 | -0, 0003 | 3, 5E-05 | -1E-06 | 0, 00053 | 7, 25E-05 | 0, 000146 |
|
|
|
Таблица 2. 6
| № опыта | z02 | z12 | z22 | z32 | z42 | z52 | z62 | z72 | z82 | z92 |
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 0, 0729 | 0, 0729 | 0, 0729 | ||||||||
| 1, 476225 | 0, 556852 | 0, 5329 | 0, 5329 | |||||||
| 1, 476225 | 0, 556852 | 0, 5329 | 0, 5329 | |||||||
| 1, 476225 | 0, 5329 | 0, 556852 | 0, 5329 | |||||||
| 1, 476225 | 0, 5329 | 0, 556852 | 0, 5329 | |||||||
| 1, 476225 | 0, 5329 | 0, 5329 | 0, 556852 | |||||||
| 1, 476225 | 0, 5329 | 0, 5329 | 0, 556852 | |||||||
| 0, 5329 | 0, 5329 | 0, 5329 | ||||||||
| Сумма |
10, 95245 |
10, 95245 |
10, 95245 |
4, 361404 |
4, 361404 |
4, 361404 |
Полиномиальная модель второго порядка для k=2 и k=3 имеет вид:
при k=2
;
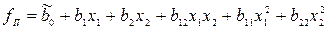при k=3
.
Расчёт всех коэффициентов кроме 
производится по формуле (2. 2), причём:
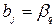, при j=q=1, 2, …, k;
, при j, u=1, 2, …, k, j< u, q=(k+1), (k+2), …, (n-k-1);
, при j=1, 2, …, k, q=(n-k-1)+j.
Таким образом:
· при k=2
, 
, , 
, 
, 
;
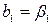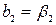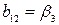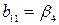· при k=3
, , 
, 
, 
, 
,
, 
, 
.
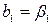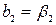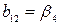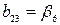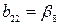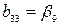Расчёт коэффициента производится по формуле:
.
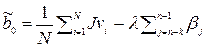В частном случае:
· 
при k=2;
· 
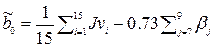при k=3.
Для рассматриваемого примера, основываясь на данных таблиц 2. 5 и 2. 6, рассчитаем значения коэффициентов и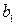 
(остальные коэффициенты определяются аналогично 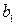по формуле (2. 2)):
,
.
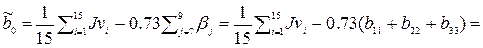
Результаты расчёта всех коэффициентов приведены в табл. 2. 7.
Таблица 2. 7
| Коэффициент |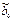 
| b1 | b2 | b3 | b12 | b13 | b23 | b11 | b22 | b33 |
| Значение | 0, 022821 | 0, 000174 | 5, 95E-06 | -0, 00052 | -3, 8E-05 | 4, 38E-06 | -1, 2E-07 | 0, 000122 | 1, 66E-05 | 3, 36E-05 |
|
|
|
Когда значения коэффициентов полинома (2. 1) найдены, необходимо приступить непосредственно к поиску минимума функции. Для этого требуется взять частные производные от функции 
по всем переменным и приравнять их к нулю. Рассмотрим данную процедуру при k=3:
;
,
,
.
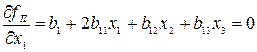Решая полученную систему, состоящую из трёх линейных уравнений и трёх неизвестных - 
, находим координаты экстремальной точки (минимума функции ) в кодированных значениях:
,
,
.
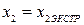Перевести значения координат в абсолютные можно по следующей формуле:
, j=1, 2, …, k,
где 
- абсолютное значение j – го параметра, 
- начальное значение j – го параметра, 
- интервал варьирования j – го параметра, 
- координата экстремальной точки, соответствующая j – му параметру (кодированное значение).
Для рассматриваемого примера:
, 
,
, 
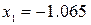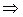
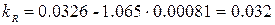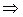
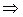
с,
, 
с.
При подстановке полученных значений параметров регулятора в модель Simulink, получаем искомое значение функционала качества, отвечающее координатам найденной экстремальной точки:
JV = 0. 01965.
|
|
|
