 |
1.2. Рекомендации по выполнению
|
|
|
|
1. 2. Рекомендации по выполнению
С целью упрощения ручных расчётов алгоритм решения задачи минимизации функционала по методу наискорейшего спуска (в пределах одного цикла) реализован в специальной программе quick_descent, написанной с помощью средств MathLab. Текст программы приведён ниже:
%Описание переменных
%k - число варьируемых параметров
%param - строка начальных значений параметров
%dparam - строка шагов варьирования параметров
%opits - число опытов
%p - матрица планирования
%Jv_plan - вектор результатов эксперимента
%Jv - вектор значений функционала качества при движении по градиенту
%Lb - базовый шаг движения
%L - строка значений шагов движения для варьируемых параметров
%b - строка значений коэффициентов полиномиальной модели
%h - номер шага при движении по градиенту
%point - координаты текущей точки на траектории при движении по градиенту
%old_points - архив координат точек при движении по траектории
%q, i, j, stroka, vector, basis, num - вспомогательные переменные
%Ввод исходных данных
k=3;
param=[0. 1 0. 05 2];
dparam=[0. 024 0. 0125 1];
opits=2^k;
%Генерирование матрицы планирования средствами MathLab, состоящей из нулей и единиц
pl=ff2n(k);
%Преобразование матрицы планирования в необходимую форму
for j=1: k, p(1: opits, j)=pl(1: opits, (k+1-j));
end;
%Преобразование матрицы планирования из вида с нулями и единицами
%в вид с единицами и минус единицами
for i=1: opits,
for j=1: k,
if p(i, j)==0 p(i, j)=-1;
end;
end;
end;
disp('Матрица планирования: '); p,
%Процесс моделирования
for i=1: opits,
set_param('model/Subsystem',
'Kr', num2str((param(1)+(dparam(1)*p(i, 1)))),
'Tr1', num2str((param(2)+(dparam(2)*p(i, 2)))),
'Tr2', num2str((param(3)+(dparam(3)*p(i, 3))))),
|
|
|
sim model, Jv_plan(i, 1)=simout(end);
end;
disp('Вектор результатов эксперимента: '); Jv_plan,
%Единичная строка
for i=1: opits,
stroka(i)=1;
end;
%Вычисление коэффициента b0
b(1, 1)=stroka*Jv_plan/opits;
%Вычисление остальных коэффициентов bj, j=1, 2, 3,..., k
for i=1: k,
for j=1: opits,
stroka(j)=p(j, i); %строка с элементами столбца i-ого
%параметра матрицы планирования
end;
b(1, (i+1))=stroka*Jv_plan/opits;; %непосредственно вычисление коэффициентов
end;
disp('Коэффициенты полиномиальной модели: '); b,
%Формирование вектора результатов перемножения bi*dXi
%Нахождение максимального элемента вектора vector
%num - порядковый номер базового параметра в векторе
for i=1: k,
vector(i)=b(1, (i+1))*dparam(i);
if i==1 basis=vector(i); num=i;
elseif vector(i)< basis basis=vector(i); num=i;
end;
end;
%Базовый шаг движения
Lb=0. 5*dparam(num);
disp('Базовый шаг движения: '); Lb,
%Шаги движения Li для варьируемых параметров, i=1, 2, 3
for i=1: k,
L(i)=(b(1, (i+1))*dparam(i)*Lb)/(abs(b(1, (num+1))*dparam(num)));
end;
disp('Шаги движения варьируемых параметров: '); L,
q=1;
h=1;
%Движение по градиенту до наименьшего значения функционала качества
while (q==1),
for i=1: k,
point(i)=param(i)-(h-1)*L(i); old_points(h, i)=point(i);
end;
set_param('model/Subsystem', 'Kr', num2str(point(1)),
'Tr1', num2str(point(2)),
'Tr2', num2str(point(3)));
sim model;
Jv(h, 1)=simout(end);
if (h==1);
elseif (Jv(h, 1)> Jv((h-1), 1)) q=0;
end;
h=h+1;
end;
disp('Наименьшее значение функционала качества: '); Jv((h-2), 1),
Программа quick_descent используется применительно к модели, построенной в Simulink и отвечающей решаемой задаче в соответствии со структурной схемой, изображенной на рис. 1. 2. Один из вариантов такой модели представлен на рис. 1. 4.
Рис. 1. 4
В случае использования данной модели, для подсистемы “REGULATOR” необходимо в качестве параметров маски ввести обозначения варьируемых переменных (параметров регулятора). Для этого нужно нажать правой кнопкой мыши (ПКМ) на подсистему “REGULATOR” с целью вызова контекстного меню, выбрать пункт “Edit mask” и в открывшемся окне перейти на вкладку “Parameters”. Далее следует добавить новый параметр с помощью кнопки 
. В поле “Prompt” вводится название параметра, отображаемое в диалоге, а в поле “Variable” заносится его обозначение, которое должно точно соответствовать обозначениям данного параметра как в самой модели, так и в программе.
|
|
|
Чтобы воспользоваться программой quick_descent для решения задачи минимизации функционала, необходимо сделать изменения в её тексте в соответствии с исходными данными:
1. ввести количество варьируемых параметров k;
2. ввести начальные значения варьируемых параметров в формате:
param=[X11 X21 … Xk1], где Xj1 – начальное значение j – ого параметра;
3. ввести шаги варьирования параметров в формате:
dparam=[Δ X1 Δ X2 … Δ Xk], где Δ Xj – шаг варьирования j – ого параметра (натуральное значение);
4. в местах, где встречается функция set_param() (в процессе моделирования и при движении по градиенту), в её теле требуется указать данные в формате:
set_param(‘[ИмяФайлаМодели]/[ИмяПодсистемыРегулятора]’,
‘[Обозначение1-огоПараметра]’, ’[Значение1-огоПараметра]’, …
‘[Обозначениеk-огоПараметра]’, ’[Значениеk-огоПараметра]’),
причём вместо значений параметров необходимо вставлять выражения, аналогичные, приведённым в тексте программы.
Для выполнения пункта 2 необходимо определить начальные значения параметров регулятора, что предлагается выполнить с использованием метода логарифмических амплитудно-фазовых частотных характеристик (ЛАФЧХ). Начальные значения параметров регулятора необходимо подобрать так, чтобы желаемая ЛАХ имела частоту среза не меньше 
, наклон характеристики в области 
составлял -20дБ на декаду, а протяжённость данного участка – не менее 1, 5-2 октавы слева и справа от .
Построение ЛАХ в MatLab может быть эффективно выполнено с помощью Simulink LTI-Viewer. Для этого необходимо выполнить команду “Tools\Linear Analysis... ” окна Simulink-модели. В результате выполнения команды откроется окно “Model_Inputs_and_Outputs” как это показано на рис. 1. 5, а также пустое окно Simulink LTI-Viewer (рис. 1. 6).
Рис. 1. 5
Рис. 1. 6
Далее следует установить блок Input Point на входе и блок Output Point на выходе исследуемой системы, как это показано на рис. 1. 7 (для примера в качестве системы взят объект варианта №30 из приложения).
|
|
|
Рис. 1. 7
Для получения ЛАХ системы необходимо выполнить команду “Edit\Plot Configuration... ” в окне LTI Viewer. В результате выполнения этой команды откроется окно Plot Configuration, показанное на рис. 1. 8.
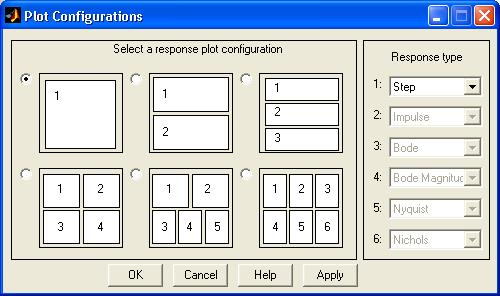
Рис. 1. 8
В открывшемся окне можно выбрать число отображаемых графиков (панель Select a response plot configuration) и их вид (панель Response type). Для построения доступны следующие графики (диаграммы):
· step – Реакция на единичное ступенчатое воздействие.
· impulse – Реакция на единичное импульсное воздействие.
· bode – Логарифмические амплитудная и фазовая частотные характеристики.
· bode mag – Логарифмическая амплитудная частотная характеристика.
· nyquist – Диаграмма Найквиста.
· nichols – Годограф Николса.
· sigma – Сингулярные числа.
· pole/zero – Нули и полюса системы.
Рекомендуется выбрать отображение одного графика с типом bode. В обновившемся окне LTI-Viewer появятся два поля для построения логарифмических амплитудных и фазовых частотных характеристик. В контекстном меню можно включить отображение сетки, установив галку рядом с пунктом Grid. Далее следует выполнить команду “Simulink\Get_Linearized_Model” в окне LTI-Viewer. Результат выполнения команды приведён на рис. 1. 9.
Рис. 1. 9
С помощью команды “Edit\Viewer Preferences…” выполняются настройки отображения диаграмм:
· установка единиц измерения по осям осуществляется на вкладке Units;
· установка интервала частот для расчета частотных характеристик осуществляется на панели Frequency Vector (вкладка Parameters); вектор частоты может быть вычислен в автоматическом режиме, при активации пункта Generate automatically.
Координату любой точки кривой можно определить, щелкнув левой клавишей мыши на соответствующую точку диаграммы.
Таким образом, получив ЛАХ изучаемого объекта, подбираем начальные значения параметров регулятора для реализации желаемой ЛАХ в соответствии с вышеизложенными рекомендациями. Для рассматриваемого примера (вариант №30)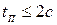 
, тогда 
. Далее подбираем значения параметров регулятора, удовлетворяющие поставленным требованиям к желаемой ЛАХ. Для рассматриваемого варианта параметры регулятора имеют следующие начальные значения: 
. Логарифмические амплитудная и фазовая частотные характеристики объекта, регулятора и разомкнутой системы (РС) приведены на рис. 1. 10. На рис. 1. 11 приведена модель Simulink, на основе которой были получены данные характеристики.
|
|
|
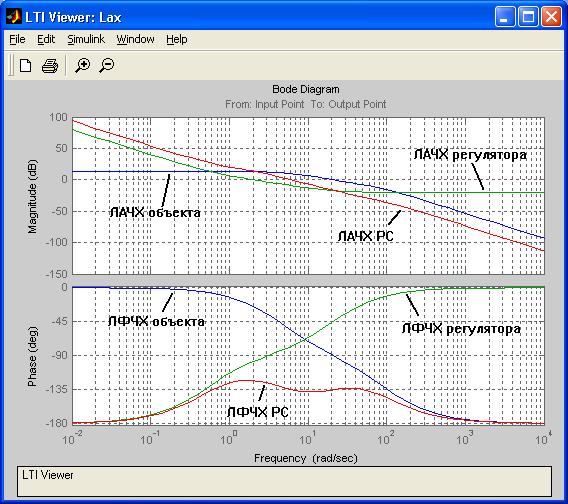
Рис. 1. 10
Рис. 1. 11
При определённых подсистемах “OBJECT” и “REGULATOR” для построения всех ЛАФЧХ в одном поле необходимо соблюдать следующие действия: сначала установить в элементе “Constant” значение 1 (для подключения к элементу “Output Point” первой цепи - подсистемы “OBJECT”); далее в окне LTI-Viewer выполнить команду “Simulink\Get_Linearized_Model” – будет построена ЛАФЧХ объекта. Остальные ЛАФЧХ строятся аналогичным образом с изменением значений в элементе “Constant”. Для удаления ненужных ЛАФЧХ нужно выполнить команду “Edit\Delete Systems…” и выбрать ЛАФЧХ для удаления.
Выбрав начальные значения параметров регулятора, перейдём к рассмотрению примера использования программы quick_descent для решения задачи минимизации. Возьмём исходные данные из варианта №30, тогда объект будет представлен звеном второго порядка с передаточной функцией:
,
где 
=0. 23с,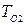 
=0. 01с, 
=5. Детализированная структурная схема объекта приведена на рис. 1. 12 в виде маскированной подсистемы Simulink.
Рис. 1. 12
Регулятор представлен двумя ПИ – регуляторами, соединёнными последовательно, и имеет следующие параметры: 
. В виде маскированной подсистемы регулятор изображён на рис. 1. 13.
Рис. 1. 13
В качестве эталонной модели взята стандартная форма Баттерворта 3-го порядка с передаточной функцией:
,
где 
- параметр, характеризующий быстродействие эталонной модели, определяется из соотношения 
, где 
- нормированное время, причём для вышеуказанных эталонных моделей:
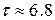при n=2;
при n=3;
при n=4.
Для рассматриваемого примера 
. Детализированная структурная схема эталонной модели представлена на рис. 1. 14.
Рис. 1. 14
Рассмотрим применение программы quick_descent для данного примера. Чтобы начать решение задачи с помощью программы quick_descent, введём изменения в её тексте:
· количество варьируемых параметров k=3;
· начальные значения параметров найдены ранее: , то есть param=[0. 1 0. 05 2];
· приращения варьируемых параметров выбираются из следующего условия: по отдельности они должны давать примерно одинаковый вклад в изменение функционала качества; основываясь на сказанном, выбираем приращения рассматриваемых переменных: 
, то есть dparam=[0. 024 0. 0125 1];
|
|
|
· остальные изменения в тексте программы уже учтены.
Таким образом, исходные данные для решения требуемой задачи представлены в табл. 1. 2.
Таблица 1. 2
| Варьируемая переменная |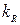 
| 
| 
|
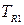
| Основной уровень | 0. 1 | 0. 05 | |
| Интервал варьирования | 0. 024 | 0. 0125 | |
| Верхний уровень | 0. 124 | 0. 0625 | |
| Нижний уровень | 0. 076 | 0. 0375 |
Далее, поместив файл текста программы в папку с файлом модели и установив соответствующий текущий каталог в окне MatLab, в командной строке MatLab вводится имя программы quick_descent и нажимается Enter для её выполнения. Конечным результатом расчётов программы является минимальное значение функционала качества на данном цикле метода наискорейшего спуска, которое выводится на экран и может быть найдено, как и значения всех остальных переменных, используемых в программе, в рабочей области MatLab (Workspace). Помимо этого программа выдаёт результаты промежуточных вычислений. Используя последние вместе с данными из рабочей области можно восстановить весь ход процесса поиска минимума функции. В нашем случае он будет выглядеть следующим образом:
1. Сначала была создана матрица планирования и проведён полный факторный эксперимент (см. табл. 1. 3).
Таблица 1. 3
|
Номер опыта |
Матрица планирования |
Значение Jv | |||
| x0 | x1 ( )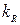
| x2 ( )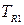
| x3 ( )
| ||
| +1 | -1 | -1 | -1 | 0, 34932 | |
| +1 | +1 | -1 | -1 | 0, 40039 | |
| +1 | -1 | +1 | -1 | 0, 22867 | |
| +1 | +1 | +1 | -1 | 0, 31944 | |
| +1 | -1 | -1 | +1 | 0, 28557 | |
| +1 | +1 | -1 | +1 | 0, 35419 | |
| +1 | -1 | +1 | +1 | 0, 1675 | |
| +1 | +1 | +1 | +1 | 0, 26503 | |
2. Далее определяются коэффициенты полиномиальной модели:
, 
, 
, 
.
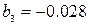3. После выбора в качестве базовой переменной x3 , рассчитывается базовый шаг движения λ б = 0. 5 и вычисляются шаги движения по всем переменным:
λ 1 = 0. 016, λ 2 = -0. 011, λ 3 = -0. 5.
4. На последнем этапе происходит движение по траектории в направлении градиента функции (см. табл. 1. 4):
Таблица 1. 4
| Шаг | x1 ( )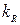
| x2 ( )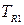
| x3 ( )
| Значение Jv |
| 0. 1 | 0. 05 | 0. 28826 | ||
| 0. 084 | 0. 061 | 2. 5 | 0. 19818 | |
| 0. 067 | 0. 073 | 0. 11158 | ||
| 0. 051 | 0. 084 | 3. 5 | 0. 048019 | |
| 0. 034 | 0. 095 | 0. 045294 | ||
| 0. 018 | 0. 107 | 4. 5 | 0. 25479 |
Из табл. 1. 4 видно, что наименьшее значение функционала JV=0. 045294.
Второй цикл проводится аналогично. Исходные данные для второго цикла с учётом результатов первого представлены в табл. 1. 5.
Таблица 1. 5
| Варьируемая переменная |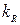
|
|
|
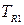
| Основной уровень | 0. 034 | 0. 095 | |
| Интервал варьирования | 0. 001 | 0. 02 | |
| Верхний уровень | 0. 035 | 0. 115 | |
| Нижний уровень | 0. 033 | 0. 075 |
Наименьшее значение функционала во втором цикле JV = 0. 027459 при 
.
На третьем цикле исходные данные так же основываются на результатах предыдущего цикла и приведены в табл. 1. 6.
Таблица 1. 6
| Варьируемая переменная |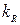
|
|
|
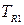
| Основной уровень | 0. 0347 | 0. 065 | |
| Интервал варьирования | 0. 004 | 0. 008 | |
| Верхний уровень | 0. 0387 | 0. 073 | |
| Нижний уровень | 0. 0307 | 0. 057 |
Наименьшее значение функционала в третьем цикле JV = 0. 022848 при 
.
Дальнейший поиск минимума функционала качества методом наискорейшего спуска становится неэффективным вследствие увеличения кривизны поверхности отклика при приближении к экстремуму, поэтому продолжить решение задачи минимизации рекомендуется с помощью метода, позволяющего оценить поверхность отклика вблизи экстремума полиномом второго порядка.
|
|
|
