 |
3.2. Рекомендации по выполнению
|
|
|
|
Математическое описание поставленной задачи приведено в виде структурной схемы Simulink на рис. 1. 4. В качестве конкретного задания продолжает рассматриваться вариант №30 из приложения, поэтому объект и регулятор остаются такими же как и в предыдущих работах.
Модель реакции на управляющее воздействие соответствует стандартной форме Баттерворта 3-его порядка и представлена на рис. 1. 4 подсистемой “MODEL”, имеющей следующее содержание (см. рис. 3. 1):
Рис. 3. 1
Значение параметра, характеризующего быстродействие модели на начальном этапе решения задачи, примем в соответствии с вышеизложенными рекомендациями, то есть 
= 4. 5 с-1 (результат взят из расчётов, проведённых в работе №1).
Для нахождения минимума функции нескольких переменных в MatLab имеются специальные средства, отличающиеся друг от друга алгоритмами поиска экстремума и количеством варьируемых параметров. Для решения поставленной задачи минимизации функционала будем использовать метод деформированного многогранника. В MatLab для этой цели используется функция MINSEARCH, она имеет следующий синтаксис:
x = minsearch ( fun, x0, ∆ х, wait [, options]),
где
· x – n-мерный вектор (n – число варьируемых параметров).
· fun – подлежащая минимизации функция; это есть некая функция, которая принимает вектор х и возвращает скаляр f, как целевую функцию от х; функция fun может быть определена, как описатель функции:
x=minsearch(@myfun, x0),
где myfun есть некая функция MatLab, такая что function f = myfun(x).
· x0 – вектор начальных значений варьируемых параметров.
· ∆ х – вектор шагов варьирования параметров.
· wait – если установлено значение wait = 1, то переход на каждую следующую итерацию осуществляется по усмотрению пользователя; при wait = 0 процесс оптимизации выполняется автоматически.
|
|
|
· options – параметры опций; параметры оптимизационных опций:
Display - уровень отображения, 'off' отображение не производится,
'iter' отображение проводится на каждой итерации, 'final'
отображение только конечной информации, 'notify'
(принимается по умолчанию) отображение только в
случае, если функция не сходится;
MaxIter - максимальное число допустимых итераций;
TolX - конечное допустимое отклонение по значению х;
options=optimset('param1', value1, 'param2', value2,... ) - создание или редактирование структуры параметров опций оптимизации.
Применительно к рассматриваемому случаю:
· n = 3;
· функцию fun определяем, как описатель функции fun=@myfun, где myfun – есть функция MatLab, написанная пользователем (текст приведён ниже);
· x0 = [ 0. 1; 0. 05; 2 ];
· ∆ х = [ 0. 01; 0. 005; 1. 5 ] – приращения варьируемых параметров выбраны в соответствии с рекомендациями, изложенными в работе №1;
· wait = 1 – остановка процесса оптимизации после каждой итерации;
· options = optimset(' Display ', ' iter ', ' MaxIter ', 60) - отображение проводится на каждой итерации, максимальное число допустимых итераций 60.
Текст пользовательской функции myfun (файл myfun. m):
% myfun – имя пользовательской функции и файла myfun. m
% model. mdl – файл модели Simulink
% Subsystem – название подсистемы регулятора
% Kr, Tr1, Tr2 – варьируемые параметры
% set_param() – функция установки значений параметров маски подсистемы
% num2str() – функция преобразования числа в строку
% x – вектор значений текущих параметров
% x(i, 1) – значение i-ого параметра на данной итерации
function rez=myfun(x); %Определение пользовательской функции
%Установка значений параметров
set_param('model/Subsystem', 'Kr', num2str(x(1, 1)),
|
|
|
'Tr1', num2str(x(2, 1)),
'Tr2', num2str(x(3, 1)));
sim ('model'); %Запуск моделирования
rez=simout(end); %Возврат конечного значения функционала
Файл пользовательской функции необходимо поместить в каталог файла модели.
Для запуска процесса оптимизации по выбранному методу, необходимо открыть файл модели и ввести в командной строке MatLab функцию поиска минимума в соответствии с её синтаксисом:
x = minsearch (@myfun, [0. 1; 0. 05; 2], [0. 01; 0. 005; 1. 5], 1,
optimset('Display', 'iter', 'MaxIter', 60))
Ход процесса оптимизации в графическом виде можно наблюдать на осциллографе, а в командном окне MatLab будут выдаваться результаты оптимизации на каждой итерации.
Параметры регулятора на определённом этапе решения поставленной задачи считаются подобранными, если удалось уменьшить значение функционала качества и добиться адекватного совпадения реакции системы на ступенчатое управляющее воздействие с эталонной моделью.
Для рассматриваемого примера осциллограммы переходных процессов (ПП) при 
до (JV=0. 2882) и после (JV=0. 0071) оптимизации представлены на рис. 3. 2 и 3. 3 соответственно.
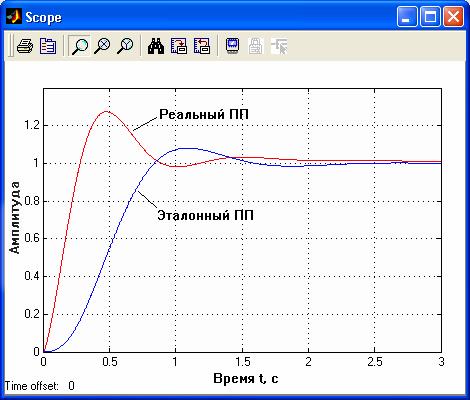
Рис. 3. 2
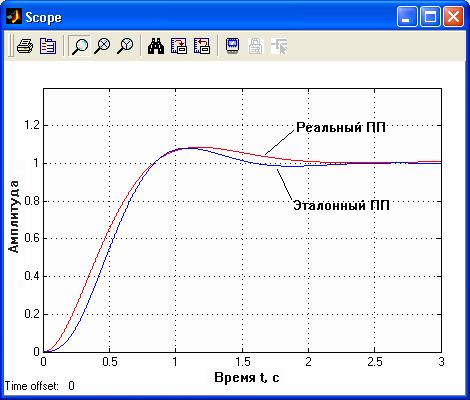
Рис. 3. 3
Значения параметров регулятора после оптимизации: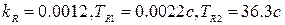 
. Число итераций - 51.
Так как оптимизация при начальном быстродействии эталонной модели ( ) осуществлена вполне успешно, необходимо увеличить быстродействие эталона вдвое и выполнить заново весь процесс оптимизации. При достижении положительных результатов данную процедуру повторяют вновь и вновь. Критерий остановки данного процесса был рассмотрен ранее. Таким образом, для рассматриваемого примера после ряда подобных циклов оптимизации было получено конкретное значение параметра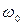 
, при котором ещё выполняется первое условие поставленной задачи. Другими словами при 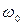= 100с-1 результаты оптимизации ещё остаются положительными, но при дальнейшем увеличении быстродействия реакция выходной переменной на ступенчатое управляющее воздействие не совпадает с аналогичной, заданной эталонной моделью.
Осциллограммы переходных процессов после последнего цикла оптимизации (при 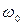= 100с-1) представлены на рис. 3. 4.
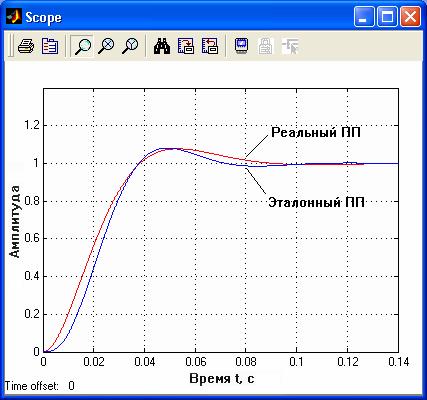
Рис. 3. 4
Значение функционала качества в данном случае: JV=0. 0003. Число итераций – 44. Параметры регулятора оптимизированной в соответствии с поставленной задачей системой имеют следующие значения: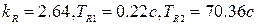 
.
|
|
|
|
|
|
