 |
3. 3. Требования к отчёту. 3. 4. Контрольные вопросы. 4. Алгоритм программы quick_descent для поиска минимума функционала по методу наискорейшего спуска
|
|
|
|
3. 3. Требования к отчёту
В отчёте следует привести: цель работы; описание задачи и этапов её решения; структурную схему эталонной модели; текст пользовательской функции; функцию MINSEARCH в соответствии с ее синтаксисом; осциллограммы переходных процессов до и после оптимизации.
3. 4. Контрольные вопросы
1. Какие средства используются в Matlab для поиска экстремума функции нескольких переменных, опишите синтаксис функции MINSEARCH?
2. В какой форме необходимо определить пользовательскую функцию, чтобы использовать её в MINSEARCH?
3. Опишите алгоритм решения поставленной в работе задачи.
4. АЛГОРИТМ ПРОГРАММЫ QUICK_DESCENT ДЛЯ ПОИСКА МИНИМУМА ФУНКЦИОНАЛА ПО МЕТОДУ НАИСКОРЕЙШЕГО СПУСКА
В алгоритме приняты следующие обозначения:
· k - число варьируемых параметров;
· param[1 x k] - строка начальных значений параметров;
· dparam[1 x k] - строка шагов варьирования параметров;
· opits - число опытов;
· pl[opits x k] - матрица планирования, генерируемая средствами Matlab;
· p[opits x k] - матрица планирования, используемая в расчетах;
· JV_PLAN [opits x 1] - вектор результатов эксперимента;
· h - номер шага при движении по градиенту;
· JV [hm x 1] - вектор значений функционала качества при движении по градиенту, hm - общее число шагов на данном цикле;
· varn – значение n-го варьируемого параметра, n=1, 2, …, k;
· lБ - базовый шаг движения;
· l[1 x k] - строка значений шагов движения для варьируемых параметров;
· b[1 x (k+1)] - строка значений коэффициентов полиномиальной модели;
· point[1 x k] - координаты текущей точки на траектории при движении по градиенту;
· old_points[hm x k] - массив координат точек при движении по траектории;
· q, i, j, num - вспомогательные переменные;
|
|
|
· vector[1 x k] - вспомогательный массив.
4. 1. Основной алгоритм
Основной алгоритм приведен на рис. 4. 1.
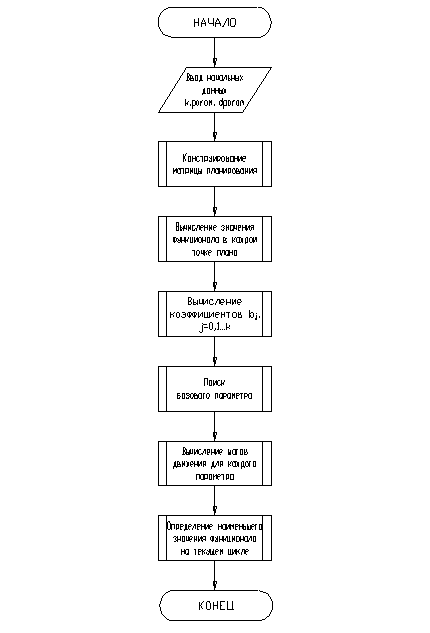
Рис. 4. 1
4. 2. Подпрограмма “Конструирование матрицы планирования”
Алгоритм подпрограммы “Конструирование матрицы планирования” приведен на рис. 4. 2.
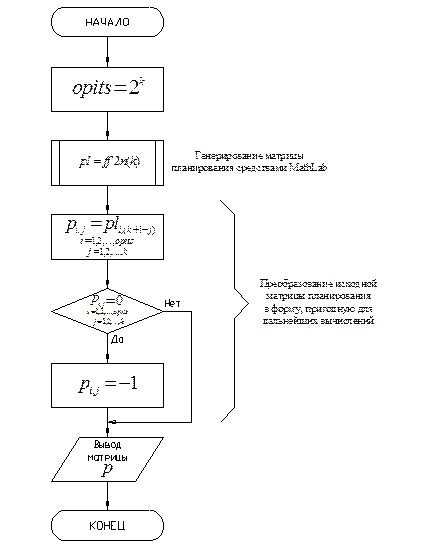
Рис. 4. 2
4. 3. Подпрограмма “Вычисление значения функционала в каждой точке плана”
Алгоритм подпрограммы “Вычисление значения функционала в каждой точке плана” приведен на рис. 4. 3.
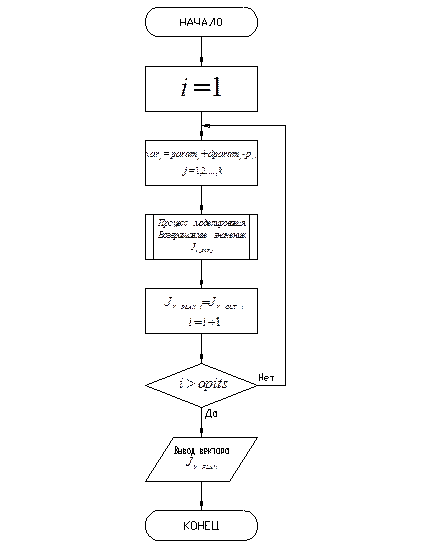
Рис. 4. 3
4. 4. Подпрограмма “Вычисление коэффициентов bj, j=0, 1... k”
Алгоритм подпрограммы “Вычисление коэффициентов bj, j=0, 1... k” приведен на рис. 4. 4.

Рис. 4. 4
4. 5. Подпрограмма “Поиск базового параметра”
Алгоритм подпрограммы “Поиск базового параметра” приведен на рис. 4. 5.

Рис. 4. 5
4. 6. Подпрограмма “Вычисление шагов движения для каждого параметра”
Алгоритм подпрограммы “Вычисление шагов движения для каждого параметра” приведен на рис. 4. 6.

Рис. 4. 6
4. 7. Подпрограмма “Определение наименьшего значения функционала на текущем цикле”
Алгоритм подпрограммы “Определение наименьшего значения функционала на текущем цикле” приведен на рис. 4. 7.
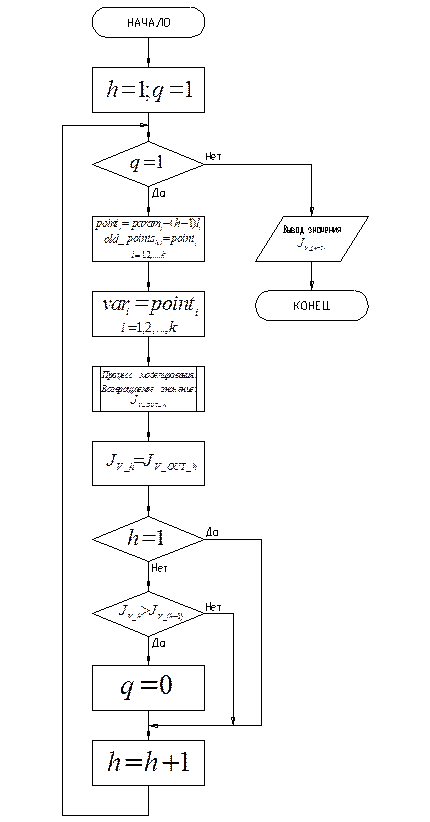
Рис. 4. 7
ЗАКЛЮЧЕНИЕ
Рассмотренные в методических указаниях методы поиска экстремума целевой функции достаточно хорошо освещены в соответствующей литературе. Особенность их изучения состоит в том, что алгоритмы поиска экстремума функции осваиваются применительно к задаче параметрической оптимизации систем управления. Суть такого подхода заключается в поиске минимума сформированного определенным образом функционала качества. Однако, аналитическая зависимость упомянутого функционала от варьируемых переменных чаще всего либо вообще не известна, либо трудноописуема. Поэтому величина функционала при определенных значениях параметров получается экспериментально. В рассматриваемых работах это делается довольно просто при описании изучаемой системы в виде модели Simulink.
|
|
|
Методы могут быть легко адаптированы практически к любой структуре системы. Это достигается раздельным описанием алгоритмов поиска экстремума целевой функции и самой системы. Так, например, в третьей работе для адаптации функции MINSEARCH к конкретной модели Simulink применяется специальная функция, написанная средствами Matlab и доступная для понимания неопытному пользователю. Используемая в первой работе программа quick_descent позволяет ограничиться лишь некоторыми изменениями в ее тексте для привязки к определенной системе.
|
|
|


