 |
Представление множеств в приложениях на Delphi
|
|
|
|
Тип множество задает неупорядоченную совокупность неповторяющихся объектов. Переменная типа множество – это совокупность объектов из исходного заданного множества – может иметь значение «пусто» (пустое множество). Число элементов исходного множества ограничено – оно не может быть более 256. Для задания элементов множества может использоваться любой порядковый тип, однако порядковые номера элементов множества, т. е. значения функции ord, должны находиться в пределах от 0 до 255. Для задания типа множества используется следующее объявление [22]:
Type <Имя> = set of <тип элементов>;
При задании типа элементов необходимо соблюдать ограничения, указанные выше.
Type A = set of Char; A1 = set of ‘A’.’Z’;
Oper = set of (Plus, Minus, Mult, Divide);
Number = set of Byte; D = set of 1..20;
Для переменных типа множество можно задавать типизированные константы. При этом значения задаются в виде конструктора множества.
Const K:D = [5,9,11,17]; R:D = [1.. 9,13,20];
Для задания значений переменным типа множество также можно использовать конструкторы. Пусть объявлено
Var AA:A;, тогда возможна запись (тип A объявлен выше)
AA:=[Char(13), Char(7), ‘0’, ‘Q’];
Если требуется присвоить этой переменной значение «пусто», то используется такой конструктор: AA:= [];
Операции над множествами
Как и для других типов, имеется ряд встроенных операций для типа множество. Пусть заданы следующие типы и переменные: Type Mn = set of 1..50; Var A, B, C: Mn;
Пусть переменным присвоены значения:
A:= [3,5,9,10]; B:= [1,7,9,10];
Объединение множеств
C:=A+B; {1,3,5,7,9,10}
Разность (A - B <> B-A)
C:=A-B; {3,5}
C:=B-A; {1,7}
Пересечение (умножение)
C:=A*B; {9,10}
Проверка эквивалентности, например в операторе IF
(A = B) {False}
Проверка неэквивалентности
|
|
|
(A <> B) {True}
Проверка, является ли одно множество подмножеством другого
(A>=B) {False}
(A<=B) {False}
Проверка, входит ли заданный элемент в заданное множество
(3 in A) {True}
(3 in B) {False}
Стандартные подпрограммы для выполнения некоторых действий над множествами
Exclude (A, 3); удалить из множества A элемент 3}
Include (A, 3); {вставить элемент 3 в множество A}.
Характеристический вектор множества
Характеристическим вектором V x множества X, заданного на универсальном множестве I, является вектор, содержащий 0 и 1. Количество элементов в векторе V x равно количеству элементов в универсальном множестве, причём, 1 записывается в случае, если элемент присутствует и в универсальном множестве I, и в множестве X, в противном случае записывается 0. Некоторые задачи с множествами, особенно на компьютере, удобно решать, используя характеристические векторы [1].
Действия над векторами похожи на логические операции.
Над характеристическими векторами выполняются поразрядно логические операции:
при пересечении – логическое умножение;
при объединении – логическое сложение;
при нахождении дополнения – значения в исходном векторе изменяются на противоположные.
При объединении множеств 
элементы характеристического вектора считают по правилу:
2) При пересечении множеств 
элементы характеристического вектора считают по правилу:
3) При нахождении дополнения 
нули меняют на единицы, единицы – на нули;
4) При нахождении симметричной разности 
, используют формулу:
Пример 2.5 Пусть I = {1, 2, 3, 4, 5, 6}, А={1, 2, 4, 5} и В={3, 5} Характеристическим вектором множества А является вектор а = (1, 1, 0, 1, 1, 0). Характеристический вектор множества В равен b = (0, 0, 1, 0, 1, 0).
Вычислим характеристический вектор множества A U 
. Он равен
а или (не b) = (1, 1, 0, 1, 1, 0) или (1, 1, 0 1, 0, 1) = (1,1,0,1,1,1).
|
|
|
Следовательно, A U = {1, 2, 4, 5, 6}.
Характеристический вектор множества А Δ В равен
(а и (не b)) или (b и (не а)) = ((1, 1, 0, 1, 1, 0) и (1, 1, 0, 1, 0, 1)) или
или ((0, 0, 1, 0, 1, 0) и (0, 0, 1, 0, 0, 1)) = (1, 1, 0, 1, 0, 0) или (0, 0, 1, 0, 0, 0) = (1, 1, 1, 1, 0, 0).
Таким образом, А Δ В = {1, 2, 3, 4}.
Практическая часть
Задание к работе
1. Изучить теоретический материал, включая и дополнительные сведения, представленные в теоретической части.
2. Задать самостоятельно универсальное множество X, множества A, B, C (или некоторые из них, т. к. в некоторых вариантах используются только два множества).
3. Cформировать характеристические векторы для исходных множеств и получить результирующее множество (по варианту), используя характеристические вектора.
4. Вычислить элементы результирующего множества (по варианту), используя операции над множествами.
5. Вывести результаты, полученные в пункте 3 и пункте 4.
6. Сравнить эти результаты и сделать выводы.
7. Пункты 3 и 4 выполнить двумя способами: аналитически и реализовать в виде приложения на Delphi.
Примечание:
1. Если в выражении используется операция разности или симметрической разности, то при выполнении действий с характеристическими векторами (пункт 3) заменить их другими операциями на множествах (использовать формулы из лекций и [23]).
2. При выполнении пункта 4 операцию симметрической разности заменить другими операциями, которые используются в Object Pascal.
3. В качестве дополнительного задания предлагается реализовать любой описанный в теоретической части алгоритм в виде приложения на Delphi.
Примеры выполнения
Пример 1.
1) Задание по варианту
I:={1,2,3,4,5,6,7}
Значения векторов A, B, C берутся произвольно, но с учетом, что количество элементов не должно быть больше 7.
Найти: характеристический вектор множеств A, B и C, характеристический вектор множества D – Vd, перейти от Vd к D.
2) Создать приложение в среде Delphi, которое решит данную задачу.
3) Решить задачу аналитически.
4) К защите данной работы необходимо знать теоретический материал по данной теме из лекций и методички, а также ответить на «Вопросы для самопроверки».
D= 
Аналитическое решение:
Характеристические векторы
A:={1,0,1,0,1,0,1}
B:={1,1,1,1,0,0,0}
C:={1,0,1,1,1,0,1}
Переходим от 
к D
|
|
|
D:= ={1,3}
Форма
Рисунок 2.10 – Формы с результатами
Код программы
implementation
procedure TForm1. Button1Click (Sender: TObject);
var
n, A, B, C: set of char;
s, s1, s2, s3, s11, s22, s33, s4, s44, s5, s55:string;
i:integer;
begin
s:='1234567';
n:=['1'..'7'];
A:=['1', '3', '5', '7'];
B:=['1', '2', '3', '4'];
C:=['1', '3', '4', '5', '7'];
begin
for i:=1 to 7 do
begin
if (s[i] in A) then
s1:=s1+'1'
else
s1:=s1+'0';
end;
s11:=' {'+s1+'}';
label7. Caption:=s11;
end;
begin
for i:=1 to 7 do
begin
if (s[i] in B) then
s2:=s2+'1'
else
s2:=s2+'0';
end;
s22:=' {'+s2+'}';
label12. Caption:=s22;
end;
begin
for i:=1 to 7 do
begin
if (s[i] in C) then
s3:=s3+'1'
else
s3:=s3+'0';
end;
s33:=' {'+s3+'}';
label13. Caption:=s33;
{Задаем характеристические векторы}
end;
begin
for i:=1 to 7 do
if((s1 [i])=(s2 [i])) and ((s3 [i])=(s2 [i])) and ((s3 [i])='1') then
s4:=s4+'1' else
s4:=s4+'0';
s44:=' {'+s4+'}';
label17. Caption:=s44;
{Находим Характеристический вектор
множества Vd}
end;
begin
for i:=1 to 7 do
if s4 [i]='1' then
s5:=s5+inttostr(i);
s55:=' {'+s5+'}';
label21. Caption:=s55;
{Переходим от Vd к D}
end;
end;
procedure TForm1. Button2Click
(Sender: TObject);
begin
close;
end;
end.
Варианты заданий
1) 
2) 
3) 
4) 
5) 
6)
7) 
8)
9) 
10) 
11) 
12) 
13) 
14) 
15)
16) 
17) 
18)
19) 
20) 
21) 
22) 
23) 
24) 
25) 
26) 
27) 
28) 
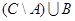
29) 
30) 
31) 
32) 
33) 
34)
35)
36) 
37) 
38) 
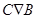
39) 
40) 
41)
42) 
43) 
44) 
45) 
46) 
47) 
47) 
49) 
50) 
Вопросы для самопроверки
1) Какие основные символы, используемые в теории множеств, вы знаете?
2) Перечислите основные операции над множествами и функции, применимые к множествам, которые используются в Delphi.
3) Что такое множество? Как его обозначить? Как можно задать множество?
4) Какое множество называют счетным? Какое – пустым?
5) Что такое подмножество?
6) Сформулируйте основные свойства счетных множеств.
7) Определите понятие вектора, булеана.
8) Сформулируйте основные аксиомы теории множеств.
9) Какие соотношения (действия) между множествами вы знаете, как они обозначаются?
10) Какое множество можно назвать универсальным?
11) Какие операции (из аналогичных арифметическим) нельзя производить с множествами?
12) Что такое диаграмма Эйлера-Венна? Проиллюстрируйте с помощью диаграмм Эйлера-Венна объединение и пересечение трех множеств.
13) Дайте определение декартова произведения множеств; какие теоремы о декартовом произведении Вы знаете?
14) Поясните термин «мощность множества».
|
|
|
15) Сформулируйте (и докажите) основные тождества алгебры множеств.
16) Дайте определение проекции вектора.
17) Что понимается под соответствием между множествами?
18) Дайте определение функции с точки зрения теории множеств. Приведите пример.
19) Дайте определение бинарного отношения, перечислите свойства.
20) Какие отношения называют рефлексивными, транзитивными?
21) Что такое «класс эквивалентности»?
22) Для чего нужна диаграмма Хассе?
23) Дайте определение нечёткого множества.
24) Какие операции допустимы над нечёткими множествами?
25) Дайте определение расстояний Хемминга и его основных свойств.
26) Перечислите основные алгоритмы генерации множеств.
|
|
|
