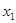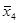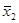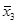|
Практическая работа № 6. Изучение методов минимизации логических функций
|
|
|
|
Цель работы: применение изученных методов минимизации логических функций для решения конкретных задач.
Краткие теоретические сведения
Общая задача минимизации логических функций сводится к построению в базисе Буля функции, содержащей минимально возможное число двоичных переменных. Исходное выражение логической функции может быть представлено формулой в любом базисе. Поэтому на первом этапе осуществляется переход к нормальной форме формулы булевой функции, как правило, совершенной дизъюнктивной нормальной форме.
F 0={×;Ú; –;Å;«;®;½;¯} – сигнатура алгебры логики;
F 1={×;Ú;–} – базис Буля;
F 2={×;–} – базис конъюнктивный;
F 3={Ú;–} – базис дизъюнктивный;
F 4={×;Å; 1} – базис Жегалкина;
F 5={¯} – базис Вебба;
F 6={½} – базис Шеффера;
F 7={®;–} – базис импликативный и т. д.
В таблицах 6.1–4 приведены формулы в некоторых базисах и для некоторых значений функции f (x 1, x 2).
Таблица 6.1 – Формулы, описывающие функции в базисах F0 и F5
| fi | Формулы в базисах F 0 и F 5 |
| f 1 | (x 1× x 2)=(x 1¯ x 2)¯(x 1¯ x 2) |
| f 6 | (x 1Å x 2)=[(x 1¯ x 1)¯(x 2¯ x 2)]¯(x 1¯ x 2) |
| f 7 | (x 1Ú x 2)=(x 1¯ x 2)¯(x 1¯ x 2) |
| f 9 | (x 1«x 2)=[ x 1¯(x 2¯ x 2)]¯[ x 2¯(x 1¯ x 1)] |
| f 13 | (x 1® x 2)=[ x 2¯(x 1¯ x 1)]¯[ x 2¯(x 1¯ x 1)] |
| f 14 | (x 1÷ x 2)=[(x 1¯ x 1)¯(x 2¯ x 2)]¯ [(x 1¯ x 1)¯(x 2¯ x 2)] |
Таблица 6.2 – Формулы, описывающие функции в базисах F0 и F2
| Fi | Формулы в базисах F 0 и F 2 |
| f 6 | (x 1Å x 2)=ù(` x 1×` x 2)×ù(x 1× x 2) |
| f 7 | (x 1Ú x 2)=ù(` x 1×` x 2) |
| f 8 | (x 1¯ x 2)=(` x 1×` x 2) |
| f 9 | (x 1«x 2)=ù(x 1×` x 2)×ù(` x 1× x 2) |
| f 13 | (x 1® x 2)=ù(x 1×` x 2) |
| f 14 | (x 1÷ x 2)=ù(x 1× x 2) |
Таблица 6.3 – Формулы, описывающие функции в базисах F0 и F3
|
|
|
| Fi | Формулы в базисах F 0 и F3 |
| f 6 | (x 1× x 2)=ù(` x 1Ú` x 2) |
| f 7 | (x 1Å x 2)=ù(` x 1Ú x 2)Úù(x 1Ú` x 2) |
| f 8 | (x 1¯ x 2)=ù(x 1Ú x 2) |
| f 9 | (x 1«x 2)=(x 1Ú x 2)Úù(` x 1Ú` x 2) |
| f 13 | (x 1® x 2)=(` x 1Ú x 2) |
| f 14 | (x 1½ x 2)=(` x 1Ú` x 2) |
Таблица 6.4 – Формулы, описывающие функции в базисах F0 и F6
| Fi | Формулы в базисах F 0 и F 6 |
| f 1 | (x 1× x 2)=(x 1½ x 2)½(x 1½ x 2) |
| f 6 | (x 1Å x 2)=[ x 1½(x 2½x2)]½[ x 2½ (x 1½ x 1)] |
| f 7 | (x 1Ú x 2)=(x 1½ x 2)½(x 1½ x 2) |
| f 8 | (x 1¯ x 2)=[(x 1½ x 1)½(x 2½ x 2)½ (x 2½ x 2)] |
| f 9 | (x 1«x 2)=[(x 1½ x 1)½(x 2½ x 2)]½ (x 1½ x 2)] |
| f 13 | (x 1® x 2)=(x 1½(x 2½ x 2). |
Практическая часть
Задание к работе
1. Минимизировать функции с помощью карт Карно или таблицы Куайна.
2. Используя средства Excel и Delphi, построить таблицы истинности заданных логических функций.
3. Сделать выводы.
Примеры выполнения
Пример 1.
Задание:
1. Минимизировать функции с помощью таблицы Куайна.
2. Используя программные средства Delphi, построить таблицы истинности заданных логических функций.
1 Минимизация с помощью таблицы Куайна:
Пусть функция F представлена в виде СДНФ
F 1СДНФ = 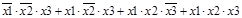
Таблица 6.5 – таблица Куайна
| х1x2x3 | 001 | 101 | 110 | 111 |
| 0 0 1 1 – 1 1 1 – | 1 | 1 | 1 | 1 |
Упростим F 1СДНФ, получим:
F 1МДНФ = 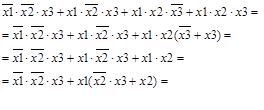
Как мы видим, результат, полученный по таблице Куайна, совпадает с F 1МДНФ.


Рисунок 6.1 – Графический интерфейс
2 Процедура основного обработчика
procedure TForm1. BitBtn1Click (Sender: TObject);
Var i:byte;
x1, x2, x3:boolean;
begin
for i:=1 to 8 do begin
StringGrid1. Cells [0, i]:=IntToStr (i‑1);
If i<=4 then StringGrid1. Cells [1, i]:='0' else StringGrid1. Cells [1, i]:='1';
If (i<=2) or ((i>=5) and (i<7)) then StringGrid1. Cells [2, i]:='0' else StringGrid1. Cells [2, i]:='1';
If (i mod 2>0) then StringGrid1. Cells [3, i]:='0' else StringGrid1. Cells [3, i]:='1';
If i<=4 then StringGrid1. Cells [4, i]:='1' else StringGrid1. Cells [4, i]:='0';
If (i<=2) or ((i>=5) and (i<7)) then StringGrid1. Cells [5, i]:='1' else StringGrid1. Cells [5, i]:='0';
x1:=StrToBool (StringGrid1. Cells [1, i]);
x2:=StrToBool (StringGrid1. Cells [2, i]);
x3:=StrToBool (StringGrid1. Cells [3, i]);
|
|
|
if (not (x1) and not (x2) and x3) or (x1 and x3) or (x1 and x2)
then StringGrid1. Cells [6, i]:='1'
else StringGrid1. Cells [6, i]:='0';
end; end;
Пример 2. Пусть будут заданы номера наборов четырех переменных, на которых логическая функция принимает единичное значение: f (2,5,6,7,10,12,13,14) =1.
Выразим эту логическую функцию в СДНФ (символ конъюнкции писать не будем):
f (0010,0101, 0110, 0111, 1010, 1100, 1101, 1110) =
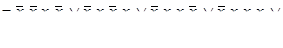 .
.
Таблица 6.6 – карта Карно для функции 4‑х переменных
|
|
|
|
|
|
|
|
| 1100 | 1110 | 0110 | 0100 |
|
|
| 1101 | 1111 | 0111 | 0101 |
|
|
| 1001 | 1011 | 0011 | 0001 |
|
|
| 1000 | 1010 | 0010 | 0000 |
|
|
|
|
|
|
|
|
Таблица 6.7 – заполненная карта

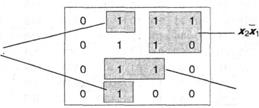
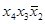
Карта Карно для четырех переменных представлена в виде таблицы 6.6. Каждая клетка карты соответствует конституенте. Заполненная карта представлена таблицы 6.7. Согласно закону склеивания, две смежные конституенты с единичными значениями всегда можно объединить для получения соответствующей импликанты. Причем смежными считаются и те, которые лежат на границах карты. Какие именно единицы требуется объединить для получения подходящей импликанты, легко определить визуально [5]. В соответствии с законом идемпотентности одна и та же единица таблицы 6.7 может склеиваться с двумя или тремя смежными единицами.
Вопросы для самопроверки
1) Перечислите законы алгебры логики, которые наиболее часто используются при упрощении сложных логических выражений?
2) Перечислите правила (следствия), полученные из законов алгебры логики, которые обычно используются при упрощении сложных логических выражений?
3) Какое логическое выражение называется конституентой?
4) Какое логическое выражение называется импликантой?
5) В чём заключается задача минимизации логической функции? Основная операция, используемая при минимизации логической функции?
6) Как выглядит карта Карно для логической функции трёх переменных? Каков принцип её построения?
7) В чём заключается смысл метода карт Карно?
8) Если логическая функция не полностью определена, то каким образом можно задать формулу, описывающую данную функцию?
9) Требует ли метод Куайна этапа предварительной (аналитической) минимизации?
10) Каким образом строится таблица Куайна?
11) По какому принципу выбираются импликанты, образующие минимизированное представление логической функции в методе Куайна?
|
|
|
12) Кратко опишите принцип, на котором базируется метод сочетания индексов.
13) Перечислите известные Вам методы минимизации логических функций.
14) Обязательным ли является условие того, что исходное выражение, описывающее логическую функцию, которое требуется минимизировать, является дизъюнктивной нормальной формой?
15) Какой из методов минимизации логических функций, на Ваш взгляд, проще поддаётся алгоритмизации?
|
|
|