 |
Практическая работа № 3. Элементы теории графов
|
|
|
|
Цель работы: изучение математических структур для представления графов, изучение наиболее известных алгоритмов на графах и построение приложений на Delphi для описания графов в виде математических структур, реализации некоторых алгоритмов на графах.
Теоретическая часть
В данном параграфе многие определения и рисунки взяты из [17] и [19], являются дополнительными сведениями для материала, рассматриваемого в [24].
Пусть V – конечное множество (множество вершин), А – множество упорядоченных пар вершин, элементы которого называются ребрами.
Тогда графом G (V, A) называется совокупность множества вершин и множества ребер. Вершины а и с соединяются ребром, если (а, с)Ì А.
Пусть дано множество вершин V и декартово произведение V х V – множество всевозможных пар вершин. Тогда графом G является подмножество декартового произведения.
Ребро графа G ориентировано, если порядок пары (a, b) существенен.
Ребро графа G не ориентировано, если порядок пары (a, b) несущественен.
Рисунок 3.1 – Ориентированный граф
Граф называется ориентированным, если все его ребра ориентированы.
Граф G называется неориентированным, если все его ребра неориентированы.
Смешанным графом называется граф, у которого есть как ориентированные, так и неориентированные ребра.
Каждому ребру E =í a, b ý можно поставить в соответствие некоторое число.
Граф G, каждому ребру которого присвоено число (например, расстояние) называется сетью.
Пусть даны a, b – вершины графа. Ребро E их соединяет. Тогда говорят, что ребро E инцидентно вершинам a и b. И обратно – вершины a и b инцидентны ребру E.
При изображении графа имеется большая свобода в размещении вершин и дуг.
|
|
|
Рисунок 3.2 – Три изображения одного и того же графа
Пусть G и G 1 графы, V и V 1 – множества их вершин соответственно. Графы G и G 1 изоморфны, если существует взаимнооднозначное соответствие между множествами их вершин V и V 1 и вершины в графе G соединены ребром в том и только том случае, если соответствующие вершины соединены ребром в графе G 1.
Если графы G и G 1 ориентированы, то направления ребер должны соответствовать друг другу. Изоморфные графы имеют одинаковые свойства.
Вершина, не инцидентная никакому ребру, называется изолированной. Граф, состоящий из изолированных вершин, называется нуль граф. Обозначается через О.
Граф, любые две вершины которого соединены ребром, называется полным графом U = U (V).
Петлей называется ребро L =(a, a). Петля считается неориентированным ребром.
Рисунок 3.3 – Петля
Пара вершин может соединяться несколькими различными ребрами.
Пара ребер Ei Ej, ориентированная в противоположном направлении, эквивалентна одному неориентированному ребру.
Таким образом, мы можем любой неориентированный граф превратить в ориентированный. При этом количество ребер увеличивается в 2 раза.
Граф называется плоским, если может быть изображен на плоскости так, чтобы его ребра пересекались только в вершинах.
Граф назовем однородным степени k, если локальные степени во всех его вершинах равны k, т. е. 
Рисунок 3.4 – Бесконечный однородный граф
| 
Рисунок 3.5 – Конечный однородный граф
|
Граф H называется частью графа G, если подмножество вершин его V (H) содержится во множестве вершин V (G) и все ребра части графа H являются ребрами G и обозначается H Ì G.
Для любой части H графа G существует дополнение 
, которое состоит из всех ребер графа G, не принадлежащих H.
|
|
Рисунок 3.6 – Граф G Рисунок 3.7 – Часть графа G
Пусть H 1 и H 2 – две части графа G. Сумма этих частей H 1U H 2 есть часть, состоящая из ребер, принадлежащих H 1 или H 2. Пересечение D = H 1 
H 2 – есть часть, состоящая из ребер, принадлежащих H 1 и H 2 одновременно. Две части не пересекаются по вершинам, если они не имеют общих вершин, и, следовательно, ребер. Части H 1 и H 2 не пересекаются по ребрам, если они не имеют общих ребер H 1 H 2=0. Если H 1 и H 2 непересекающиеся части графа G, то их сумма называется прямой и H 1U H 2= G.
|
|
|
Бинарные отношения и графы
Бинарные отношения можно изобразить графом: вершины графа – элементы множества V, ребра графа соединяют вершины, которые находятся в отношении друг к другу.
Любой граф определяет бинарное отношение R на множестве вершин V, если для каждого ребра (a, b) выполняется aRb. Нельзя говорить о взаимнооднозначном соответствии между графами и бинарными отношениями. Пустому бинарному отношению соответствует нуль-граф О. Универсальному бинарно м у отношению отвечает полный граф U. Бинарному отношению aRb, где R – отрицание R (дополнительное бинарное отношение) отвечает граф G (R)= U (V) – G (R). Обратному бинарному отношению bR * a отвечает обратный граф G (R *), т. е. граф с измененной ориентацией ребер. Операции, которые вводятся для бинарных отношений, могут быть перенесены на графы.
Симметричное бинарное отношение: если aRb, то bRa.
Рефлексивность: бинарное отношение aRa соответствует графу с петлей в каждой вершине.
Транзитивность: если aRb и bRc, то aRc. Для графа это означает, что если существует ребро (a, b) и ребро (b, c), то существует ребро (a, c). Такой граф называется связным.
Свойство связности можно рассмотреть как бинарное отношение, которое:
а) рефлексивно: вершина а связана сама с собой;
б) симметрично: если вершина а связана с вершиной b, то и вершина b связана с вершиной a;
в) транзитивно: если вершина a связана с вершиной b, и b связана с вершиной с, то вершина a связана с вершиной c.
Отношение связности есть отношение эквивалентности, т. е. оно разбивает множество вершин на попарно непересекающиеся классы.
Так как каждое множество Vi – множество связанных вершин, а вершины из разных множеств Vi не связаны, то имеем разложение графа G на части, которые не пересекаются и каждая часть – связная.
Подграфы G (Vi) называются связными компонентами графа G.
|
|
|
Каждый неориентированный граф распадается единственным образом в прямую сумму всех своих связных компонент.
Покрывающие деревья
Граф, не содержащий циклов, называется ациклическим. Деревом называется связный граф, не содержащий циклов. Пусть VG – число элементов в множестве вершин, VL – число элементов множества ребер дерева.
Рисунок 3.8 – Дерево
VG = VL ‑1
Добавим ребро – появляется цикл, удалим ребро – теряется связность. Лесом называется несвязный граф, компонентами которого являются деревья.
Пусть VL l – число элементов в множестве ребер леса, VG l – число элементов в множестве вершин леса, k – число деревьев в лесе.
VL l = VG l - k
Если дерево Т имеет корень, то дерево называется деревом с корнем. Выделим в дереве Т некоторую цепь.
Рисунок 3.9 – Дерево
Задача.
Как узнать, существуют ли циклы в графе?
Для дерева связь между числом ребер и числом вершин такова
V l= VG ‑1. Рассмотрим s= V l- VG +1, s называется цикломатическим числом. Если граф G – дерево, то s=0, если s не равно нулю, то в графе G есть циклы.
Алгоритм построения произвольного покрывающего дерева [20]
Ограничения: в графе не должно быть петель. Букетом называется произвольное дерево в графе.
Шаг 1. Выбираем произвольное ребро и помечаем его х (красим в голубой цвет).
Шаг 2. Выбираем другое произвольное непомеченное ребро. Если оба конца ребра лежат в одном букете, красим ребро в красный цвет. В противном случае – в голубой.
Шаг 3. Если все вершины графа вошли в один букет, то процедура заканчивается, т. к. помеченные голубым ребра образуют покрывающее дерево. В противном случае – перейти к шагу 2.
Рисунок 3.10 – Граф
1 шаг: (a, d) – помечаем голубым
2 шаг: (b, e) – помечаем голубым
3 шаг: (d, e) – помечаем голубым
4 шаг: (a, b) – помечаем красным
5 шаг: (a, c) – получаем голубым
Рисунок 3.11 – Дерево
Алгоритм построения минимального и максимального покрывающего дерева [21]
Пусть каждому ребру графа G присвоена длина (вес) l (x, y) (таблица 3.1). Весом дерева называется сумма весов ребер, входящих в дерево. Минимальным деревом называется дерево с минимальным весом.
|
|
|
Алгоритм формируется так же, как и алгоритм построения произвольного покрывающего дерева. Но ребра просматриваются в порядке возрастания их веса.
Таблица 3.1 – Веса ребер графа
| A | b | c | d | e | |
| a | 0 | 5 | 50 | 85 | 90 |
| b | 5 | 0 | 70 | 60 | 50 |
| c | 50 | 70 | 0 | 8 | 20 |
| d | 85 | 60 | 8 | 0 | 10 |
| e | 90 | 50 | 20 | 10 | 0 |
Порядок просмотра
(a, b) – 5 (b, e) – 50 упорядочим ребра по возрастанию
(c, d) – 8 (b, d) – 60
(d, e) – 10 (b, c) – 70
(c, e) – 20 (a, d) – 85
(a, c) – 50 (a, b) – 90
1 шаг: (a, b) – помечаем голубым
2 шаг: (c, d) – помечаем голубым
3 шаг: (d, e) – помечаем голубым
4 шаг: (c, e) – помечаем красным
5 шаг: (a, c) – помечаем голубым
Дерево построено!
Рисунок 3.12 – Дерево
Алгоритм построения максимального ориентированного дерева(алгоритм Эдмонса) [15]:
Шаг 1. Последовательно в произвольном порядке просматриваем вершины графа G 0. Просмотр вершины заключается в том, чтобы из дуг, заходящих в эту вершину, выбрать дугу с максимальным весом. При просмотре следующих вершин к уже отобранным ранее дугам добавляются новые дуги. Если добавление ребра не нарушает свойства букета, то добавление ребер продолжается. Если новое ребро образует контур, перейти к шагу 2.
Шаг 2. В случае формирования контура строится уменьшенный граф путем стягивания дуг и вершин выявленного контура исходного графа Go в одну вершину V.
В новом графе веса ребер (xi, vi) полагаются равными
l (x, vi)= l (x, y)+ l (r, s) – l (t, y),
где К – контур, а у – вершина, принадлежащая контуру.
l (x, vi) – ребро, переходящее в ребро l (x, vi)
l (r, s) – ребро, имеющее в контуре минимальный вес
l (t, y) – ребро, заходящее в вершину у и имеющее максимальный вес
Шаг 3. Выполняется тогда, когда вершины нового графа попадают в букет, а дуги образуют дерево.
Возможны 2 случая:
вершина Vo является корнем дерева, тогда необходимо рассмотреть ребра букета в новом графе совместно с ребрами контура. Удалить из рассматриваемого множества ребер ребро с минимальным весом;
если Vo не является корнем дерева – в букете нового графа имеется лишь одно ребро, заходящее в некоторую вершину Z и одно ребро контура, заходящее в ту же вершину. Удаляем ребро контура, заходящее в вершину Z.
Пример.
Рисунок 3.13 – Граф
Просмотр вершин: Букет получаемых ребер
a (da)
b (da) (cb)
c (da) (cb) (ac)
d (da) (cb) (ac) (bd)
Ребра (ac) (cb) (bd) (da) образуют контур. Минимальный вес ребра в контуре 2.
Стягиваем контур в одну вершину и рассматриваем граф:
Рисунок 3.14 – Граф
l (fe)=1
|
|
|
l (e, Vo)= l (ea)+2–3=3+2–3=2
l (f, Vo)= l (f, a)+2–3=-1
l (f, Vo) 1= l (fd)+2‑ l (b, d)=1+2–2=1
Просмотр вершин Букет ребер
e (fe)
f (fe)
Vo (f e) (eV o)
Получили множество ребер исходного графа Go такое:
(fe) (ea) – образуют букет
(ac) (cb) (bd) (da) – образуют контур
Vo не является контуром дерева, удаляем (da), поскольку (da) – ребро из контура. Получили дерево:
(fe) (ea) (ac) (cb) (bd) с весом l=1+2+3+2+2=10
Задача о кратчайших путях
Пусть G – ориентированный граф, Е – ребра графа. Каждому ребру соответствует число.
Рисунок 3.15 – Эйлеров цикл
Задача Эйлера о Кенигсбергских мостах [19]: необходимо выйти из любой точки города и вернуться в нее, при этом пройдя по каждому мосту только один раз. Эйлер свел эту задачу к графу: существует ли в конечном графе такой цикл, в котором каждое ребро участвует только один раз? Цикл, в котором каждое ребро графа G участвует всего один раз, называется эйлеровым циклом. Граф, содержащий эйлеров цикл, называется эйлеровым.
Дальнейшее развитие задачи об Эйлеровом цикле
Припишем ребрам графа длину μ (ai, aj). Требуется найти путь в графе, который проходит через все ребра и имеет наименьшую длину.
Пример.
Рисунок 3.16 – Граф
S – стартовая вершина. Из вершины S надо пройти по всем ребрам так, чтобы маршрут имел минимальную длину. Очевидно, что длина маршрута будет минимальной, если каждое ребро будет пройдено всего один раз – т. е. маршрут будет эйлеровым циклом.
Все локальные степени – четные, значит граф эйлеров.
Варианты прохождения по циклу:
1) (sa) (ab) (bc) (cd) (db) (ds)
2) (sa) (ab) (bd) (dc) (cb) (bs)
3) (sb) (bc) (cd) (db) (ba) (as)
4) (sb) (bd) (dc) (cb) (ba) (as)
Длина эйлерова цикла – 22. Любой из вариантов 1–4 содержит каждое ребро графа, следовательно, длина одинакова для всех циклов 1–4. Длина эйлерова цикла не зависит от того, какая вершина будет выбрана за исходную.
Задача поиска эйлерова цикла – это задача о: – поиске наилучшего способа прохождения бригады по дорогам; – прохождении с/х техники по полям.
Впервые эта задача рассматривалась в связи с нахождением оптимального маршрута следования почтальона, который доставляет письма своим адресатам и должен при этом пройти минимальный путь.
Алгоритм нахождения эйлерова цикла для неориентированного графа [19]:
Дан эйлеров граф – т. е. граф с четными локальными степенями.
Найдем первое ребро х, инцидентное вершине S. Затем найдем ребро, смежное с ребром х, которое не образует цикл и еще не было использовано. Продолжим этот процесс до тех пор, пока не вернемся в вершину S. Если в построенный цикл С 1 вошли все ребра графа – задача решена.
Если в построенный цикл С 1 вошли не все ребра – строим цикл С 2, состоящий из неиспользованных ребер и начинающийся с произвольного неиспользованного ребра.
Таким образом, строим циклы С 2, С 3,….Образование циклов продолжается до тех пор, пока не будут использованы все ребра.
Все циклы Сi необходимо объединить в один цикл. Условие объединения циклов С 1 и С 2 – наличие у них общей вершины х. Начинаем движение с любой вершины и двигаемся по циклу С 1 до тех пор, пока не дойдем до х. Затем проходим ребро. С» и возвращаемся в х. Продолжаем обход по оставшимся ребрам до возвращения к исходной точке. Эта процедура легко обобщается на случай любого числа объединяемых циклов.
Циклы Эйлера для ориентированного графа
Алгоритм построения эйлерова цикла в эйлеровом ориентированном графе является аналогом алгоритма построения эйлерова цикла для неориентированного графа.
Строятся циклы Сi с учетом ориентации ребер, и затем все циклы объединяются в один.
Гамильтонов цикл (задача о коммивояжере)
Простой цикл, проходящий через каждую вершину графа только один раз, называется гамильтоновым циклом.
Если ребрам приписана длина, то различные варианты циклов отличаются друг от друга. Поэтому ставится задача нахождения гамильтонова цикла, имеющего минимальную длину.
Гамильтонов цикл наименьшей длины называется оптимальным гамильтоновым циклом (ОГЦ)
Поиск оптимального гамильтонова цикла – задача о коммивояжере, который должен посетить множество пунктов и вернуться домой, пройдя наименьший путь.
Решением задачи о коммивояжере не всегда является ОГЦ.
Гамильтоновы графы применяются для моделирования многих практических задач. Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра – связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, например, расстояние между городами или время движения по дороге. Для решения задачи нам необходимо найти гамильтонов цикл минимального общего веса.
Рисунок 3.17 – Ребра, входящие в гамильтонов цикл С
К сожалению, алгоритм решения данной задачи, дающий оптимальное решение, пока не известен. Для сложных сетей число гамильтоновых циклов, которые необходимо просмотреть для выделения минимального, непомерно огромно. Однако существуют алгоритмы поиска субоптимального решения [1]. Субоптимальное решение необязательно даст цикл минимального общего веса, но найденный цикл будет, как правило, значительно меньшего веса, чем большинство произвольных гамильтоновых циклов! Один из таких алгоритмов – алгоритм ближайшего соседа.
Этот алгоритм выдает субоптимальное решение задачи коммивояжера, генерируя гамильтоновы циклы в нагруженном графе с множеством вершин V. Цикл, полученный в результате работы алгоритма, будет совпадать с конечным значением переменной маршрут, а его общая длина – конечное значение переменной w.
begin
Выбрать v? V;
маршрут:=v;
w:=0;
v':=v;
Отметить v';
while остаются неотмеченные вершины do begin
Выбрать неотмеченную вершину и,
ближайшую к v';
маршрут:= маршрут u;
w:= w + вес ребра v'u;
v':=u;
Отметить v';
end
маршрут:= маршрут v;
w:= w + вес ребра v'v;
end
Пример. Примените алгоритм ближайшего соседа к графу, изображенному на рисунке 3.18. За исходную вершину возьмите вершину D.
Рисунок 3.18 – Граф
Таблица 3.2 – Алгоритм ближайшего соседа
| и | маршрут | w | v' | |
| Исходные значения | – | D | 0 | D |
| С | dc | 3 | С | |
| А | DCA | 9 | A | |
| В | DCAB | 14 | В | |
| Последний проход | В | DCABD | 24 | В |
В результате работы алгоритма был найден гамильтонов цикл DCABD общего веса 24. Делая полный перебор всех циклов в этом маленьком графе, можно обнаружить еще два других гамильтоновых цикла: ABCDA общего веса 23 и ACBDA общего веса 31. В полном графе с двадцатью вершинами существует приблизительно 6,1 * 10^16 гамильтоновых циклов, перечисление которых требует чрезвычайно много машинной памяти и времени.
Реализация примера данного алгоритма в Delphi:
procedure TForm1. Button1Click (Sender: TObject);
const mat:array [1.. 4,1..4] of byte=((0,5,6,8), (5,0,7,10), (6,7,0,3), (8,10,3,0));
Versh:array [1..4] of char=('a', 'b', 'c', 'd');
buk:char='d';
Type t=set of 'a'..'d';
Var dlina, i, j, min, n, k, s:byte;
put:string;
z:t;
begin
dlina:=0;
Memo1. Lines. Clear;
for i:=1 to 4 do if versh[i]=buk then begin n:=i; s:=i;
include (z, buk);
put:=put+buk;
end;
for j:=1 to 3 do begin
if mat [n, 1]<>0 then begin min:=mat [n, 1]; k:=1; end
else begin min:=mat [n, 2]; k:=2; end;
for i:=1 to 4 do
if (mat [n, i]<min) and (mat [n, i]<>0) and (not (versh[i] in z)) then begin
min:=mat [n, i];
k:=i;
end;
dlina:=dlina+min;
put:=put+versh[k];
include (z, versh[k]);
n:=k;
end;
put:=put+'d';
dlina:=dlina+mat [k, s];
Memo1. Lines. Add ('маршрут:'+' '+put);
Memo1. Lines. Add ('длина маршрута='+IntToStr(dlina));
end;
end.
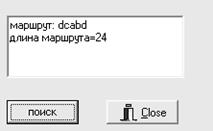
Рисунок 3.19 – Форма с результатом
Практическая часть
Задание к работе
1 изучить теоретический материал по методическому пособию [24], лекциям и записям на практических занятиях;
2 получить задание по индивидуальному варианту в виде графа или матрицы смежности, в первом случае построить матрицу смежности, во втором – нарисовать граф;
3 составить подробное описание графа: ориентированный или неориентированный, количество вершин, дуг (рёбер), содержит ли циклы и какие, найти степени вершин, количество компонент связности и т. д.;
4 создать приложение на Delphi для расчёта матрицы инцидентности по известной матрице смежности (если граф достаточно сложный, то можно взять подграф этого графа);
5 в качестве дополнительного творческого задания создать приложение на Delphi для реализации алгоритма ближайшего соседа, алгоритма Прима, алгоритма Уоршелла, алгоритма Дейкстры, алгоритма определения количества компонент связности графа и других известных алгоритмов на графах. [13], [17], [18], [19], [20], [21].
Примеры выполнения
Пример 1: По заданной матрице смежности построить матрицу инцидентности.
implementation
procedure TForm1. UpDown1Click (Sender: TObject; Button: TUDBtnType);
begin
with UpDown1 do begin
with StringGrid1 do begin
RowCount:=Position;
ColCount:=Position;
end;
StringGrid2. RowCount:=Position;
end;
end;
procedure TForm1. BitBtn1Click (Sender: TObject);
var i, j, CD, P, n:byte;
MS:array of array of byte;
MI:array of array of ShortInt;
begin
P:=StrToInt (Edit1. Text);
SetLength (MS, P, P);
CD:=0;
for i:=0 to P‑1 do for j:=0 to P‑1 do begin
MS [i, j]:=StrToInt (StringGrid1. Cells [j, i]);
if MS [i, j]=1 then inc(CD);
end;
SetLength (MI, P, CD);
for i:=0 to High(MS) do for j:=0 to CD‑1 do MI [i, j]:=0;
n:=0;
for i:=0 to High(MS) do for j:=0 to High(MS) do
if MS [i, j]=1 then begin
MI [i, n]:=1;
MI [j, n]:=-1;
inc(n);
end;
StringGrid2. ColCount:=CD;
for i:=0 to High(MS) do for j:=0 to CD‑1 do
StringGrid2. Cells [j, i]:=IntToStr (MI[i, j]);
end;
end.
Рисунок 3.20 – Форма с результатом
Пример 2: По заданной матрице смежности построить матрицу инцидентности.
var
Form1: TForm1;
const maxv=4;
type canh=record dinh1, dinh2:byte;
dodai:real; end;
dothi=record n:byte;
l:array [1..maxv, 1..maxv] of real;
x, y:set of 1..maxv;
t:array [1..maxv] of canh;
nt:byte;
it:real; end;
implementation
{$R *.dfm}
procedure TForm1. Button1Click (Sender: TObject);
var g:dothi;
min:real;
x, y, x0, y0:1..maxv;
i, j:byte;
begin memo1. Clear;
g.n:=maxv;
edit1. Text:=inttostr(maxv);
stringgrid1.cells [0,0]:=' Номер';
for i:=1 to maxv do begin
stringgrid1.cells [0, i]:=inttostr(i);
stringgrid1.cells [i, 0]:=inttostr(i); end;
g.nt:=0; g.it:=0; g.x:=[1..g.n]; g.y:=[1];
for i:=1 to maxv do
for j:=1 to maxv do g.l [i, j]:=strtofloat (stringgrid1. Cells [j, i]);
while g.nt<g.n‑1 do begin
min:=-1;
for x:=1 to g.n do
for y:=1 to g.n do
if (x in g.y) and (y in (g.x-g.y)) and (g.l [x, y]>0) then
begin
if (min=-1) or (min>g.l [x, y]) then begin
min:=g.l [x, y];
x0:=x; y0:=y; end;
end;
g.y:=g.y+[y0];
g.nt:=g.nt+1;
g.it:=g.it+min;
with g.t [g.nt] do begin
dinh1:=x0;
dinh2:=y0;
dodai:=min; end; end;
for i:=1 to (maxv‑1) do
with g.t[i] do
memo1. Lines.add ('Ребро: '+inttostr(dinh1)+inttostr(dinh2)+' '+
'Весом: '+floattostr(dodai));
end;
end.
Рисунок 3.21 – Форма с результатом
Пример 3: Составить приложение на Delphi, реалилующее алгоритм Уоршелла.
var
Form1: TForm1;
const maxv=4;
type canh=record dinh1, dinh2:byte;
dodai:real; end;
dothi=record n:byte;
l:array [1..maxv, 1..maxv] of real;
x, y:set of 1..maxv;
t:array [1..maxv] of canh;
nt:byte;
it:real; end;
implementation
{$R *.dfm}
procedure TForm1. Button1Click (Sender: TObject);
var g:dothi;
min:real;
x, y, x0, y0:1..maxv;
i, j:byte;
begin memo1. Clear;
g.n:=maxv;
stringgrid1.cells [0,0]:=' Номер';
for i:=1 to maxv do begin
stringgrid1.cells [0, i]:=inttostr(i);
stringgrid1.cells [i, 0]:=inttostr(i); end;
g.nt:=0; g.it:=0; g.x:=[1..g.n]; g.y:=[1];
for i:=1 to maxv do
for j:=1 to maxv do g.l [i, j]:=strtofloat (stringgrid1. Cells [j, i]);
while g.nt<g.n‑1 do begin
min:=-1;
for x:=1 to g.n do
for y:=1 to g.n do
if (x in g.y) and (y in (g.x-g.y)) and (g.l [x, y]>0) then
begin
if (min=-1) or (min>g.l [x, y]) then begin
min:=g.l [x, y];
x0:=x; y0:=y; end;
end;
g.y:=g.y+[y0];
g.nt:=g.nt+1;
g.it:=g.it+min;
with g.t [g.nt] do begin
dinh1:=x0;
dinh2:=y0;
dodai:=min; end; end;
for i:=1 to (maxv‑1) do
with g.t[i] do
memo1. Lines.add ('Ребро: '+inttostr(dinh1)+inttostr(dinh2)+' '+
'Весом: '+floattostr(dodai));
end;
end.
Рисунок 3.23 – Форма с результатом
Вариантв заданий
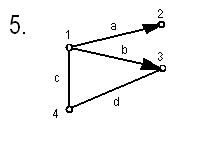
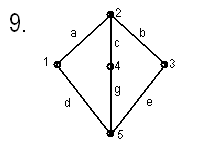
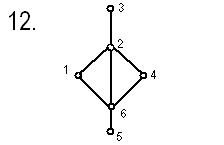
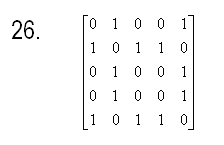
Вопросы для самопроверки
1) Какие операции над графами Вы знаете?
2) Как формируется матрица смежности?
3) Как формируется матрица весов?
4) Как формируется матрица достижимости?
5) Как формируется матрица инцидентности?
6) Перечислите основные понятия, относящиеся к графам-деревьям.
7) Приведите пример сортировки и поиска в деревьях.
8) Для чего применяется алгоритм, подобный алгоритму Дейкстры, в коммуникационных сетях?
9) Перечислите известные Вам алгоритмы обхода графов.
10) Что такое транспортная сеть? Приведите пример.
11) Какой граф называется эйлеровым? Приведите пример эйлерова графа.
12) Какой граф называется гамильтоновым? Приведите пример гамильтонова графа.
13) Какой вид отношений на графах представляет изоморфизм графов?
14) Приведите пример отношения порядка и отношения эквивалентности на графе.
15) Какие алгоритмы обхода графов Вам известны?
16) Какие виды графов Вы знаете?
17) Что понимается под степенью вершины?
18) Как определяются числа внутренней и внешней устойчивости графа?
19) Как определяются хроматическое и цикломатическое числа графа?
20) Сформулируйте транспортную задачу и связанные с ней понятия?
21) Опишите кратко алгоритм управления проектами.
22) Приведите пример построения разреза графа.
23) Приведите пример дерева с корнем.
|
|
|
