 |
1. Основное уравнение движения атмосферы
|
|
|
|
1. Основное уравнение движения атмосферы
Динамика изучает движение атмосферы под действием заданного поля силы.
При изучении атмосферных движений широко используются общие законы гидромеханики и термодинамики.
Возьмем уравнение Навье – Стокса, которое является самым общим уравнением движения для газа, где n - молекулярная вязкость.
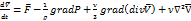
Это уравнение записано по отношению к абсолютной системе координат. Оно следует из второго закона Ньютона:
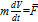
Для метеорологии это неудобно, так как нас интересует движение относительно Земли. Поэтому нужно перейти к относительному движению.
Два последних члена в уравнении обозначим через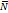 
.
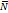– ускорение, вызванное внутренним трением жидкости.
В метеорологии играет роль не просто молекулярная вязкость n, а турбулентная вязкость. С другой стороны, роль вязкости очень мала, и сила 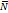в вопросах движения средней атмосферы и прогноза играет очень малую роль.
Из механики известно, что абсолютное ускорение на Земле складывается из относительного, переносного и ускорения, вызванного отклоняющей силой вращения Земли.
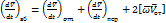
Нас интересует относительное ускорение 
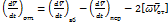
Подставим в уравнение (4) вместо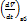 
уравнение Навье-Стокса.
(*)
В уравнении (*) все члены имеют размерность ускорения, т. е. все силы отнесены к единице массы.
Рассмотрим член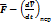 
Сила 
- напряженность поля массовых сил (для силы тяжести величина 
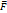равна ускорению свободного падения 
): 
|
|
|
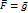
- ускорение переносного движения, вызванное вращением Земли.
- это величина центробежной силы, рассчитанной на единицу массы.
r = 6, 4× 106 м – средний радиус Земли
w = 7, 3× 10-5 1/с – угловая скорость вращения Земли
w2 r = 0, 034 м/с2
» 10 м/с2
> > w2 r, т. е. переносное ускорение не превышает 0, 3 % от ускорения силы тяжести.
Значит,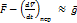 
Ускорение Кориолиса тоже невелико. Если принять Vот = 10 м/с, то
2wVот = 2× 7, 3× 10-5 1/с × 10 м/с2 » 0, 001 м/с2
По отношению к ускорению силы тяжести 
эта величина очень мала, но при горизонтальном движении роли не играет, а остается только сила Кориолиса. Поэтому при горизонтальном движении ею пренебрегать нельзя. В дальнейшем мы будем рассматривать только относительное движение, поэтому обозначение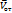 
, 
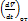не будем писать. И тогда основное уравнение движения атмосферы будет записано в таком виде:
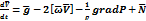
2. Основное уравнение движения в декартовой системе координат.
Обычно в теоретических рассуждениях и некоторых частных решениях применяется декартова система координат. Это прямоугольная, как правило, правовращающая система координат, связанная с вращающейся Землей. Обычно ось x направлена по параллели на восток, ось y – по меридиану на север, ось z – вертикально вверх. Она сохраняет проекции, соответствующие отношению площадей на местности и на карте, позволяет просто выполнять векторные операции и выражать производные от функции простыми соотношениями.
Декартова система координат называется еще и стандартной системой. Запишем основное уравнение движения (7) и спроектируем все члены уравнения на оси декартовой системы координат (x, y, z).
|
|
|
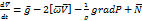
Спроектируем все члены уравнения на оси x, y, z.
; 
; 
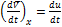Сила тяжести не имеет горизонтальной составляющей
gx = 0; gy = 0; gz = -g
Прежде чем развернуть выражение для силы Кориолиса в стандартных координатах, напомним, что собой представляет угловая скорость вращения Земли (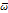 
). Это вектор, направленный по оси вращения с юга на север. Это вектор меридиональный, поэтому его проекция на ось х равна нулю, т. е. wх=0.
Другие компоненты wy и wz, лежащие в плоскости меридиана, легко выражаются через широту места j.
Рассмотрим меридиональный разрез земного шара.
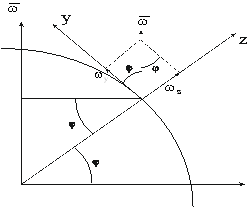
Меридиональный разрез земного шара
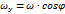
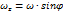
Вертикальная компонента угловой скорости вращения Земли положительна в северном полушарии и отрицательна в южном.
Запишем векторное произведение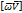 
в стандартных координатах.
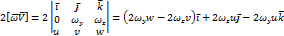
Компоненты силы Кориолиса:
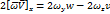
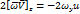
Вертикальная скорость w значительно меньше горизонтальной (u и v) w < < u, v поэтому w » 0. Учитывая связь wy и wz с w, запишем проекции силы Кориолиса на оси x, y, z.
|
|
|
