 |
- параметр Кориолиса.. 3. Основное уравнение движения в натуральных координатах.
|
|
|
|
- параметр Кориолиса.
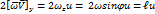
Запишем проекции на оси x, y, z силы барического градиента.
; 
; 
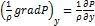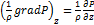
Вязкие силы в проекциях на оси x, y, z будут Nx, Ny, Nz. Теперь запишем проекции основного уравнения движения на оси декартовой (стандартной) системы:
; 
; 
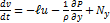Третью проекцию на ось z можно значительно упростить.
Nz < < (очень мало) g и 
Поэтому ими, по сравнению с 
, можно пренебречь. Тогда от третьего уравнения остается уравнение статики атмосферы. Эта замена называется гидростатическим приближением, или отфильтрованием мелких колебаний давления, не влияющих на погоду, на изменение давления.
Таким образом, уравнение движения в проекциях на оси декартовой системы координат:
При горизонтальном движении остаются проекции 1) и 2).
3. Основное уравнение движения в натуральных координатах.
Натуральная система координат 
тесно связана с движением. Скорость в ней направлена по касательной к траектории движения.
Ускорение частицы при произвольном горизонтальном движении в естественных координатах запишется следующим образом:
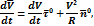
где 
- касательное (тангенциальное) ускорение
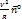- нормальное (центростремительное) ускорение.
Рассмотрим горизонтальное движение на сфере. Пусть по поверхности сферы (Земного шара) движется т. М
В любой момент это движение можно рассматривать как движение по окружности, центр которой легко найти. МС = R - радиус кривизны в точке М.
Ð МОС обозначим через a. Ось ОМ – это вертикальная ось (Z).
В точке М проведем линию горизонта. Эта линия пересекает ОС в точке С1. Линия МС1 – линия горизонта. На этой линии горизонта выберем направление нормали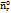 
(горизонтальная нормаль к траектории). МС1 = Rг, т. е. горизонтальный радиус, который мы обнаруживаем на карте. В точке М образуется прямоугольная правая система координат.
|
|
|
Горизонтальное движение на сфере
- это три вектора образуют правую взаимно ортогональную систему координат.
Запишем основное уравнение движения:
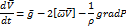
Спроектируем члены уравнения движения на горизонтальные оси естественной системы координат:
; 
Получили проекцию на касательную
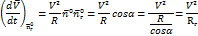
Из DСМС1:
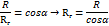
Из DСOМ:
Спроектируем правую часть на оси .
Сила тяжести не имеет горизонтальной составляющей. Поэтому единственной отличной от нуля составляющей будет вертикальная компонента силы тяжести.
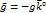
Сила Кориолиса в натуральных координатах выразится так:
Мы видим, что сила Кориолиса не имеет составляющей в направлении движения. Она лишь отклоняет частицу перпендикулярно ее траектории. Поэтому она и называется отклоняющей силой вращения Земли.
Градиент давления в естественных координатах можно представить так:
Теперь запишем проекции уравнения движения на оси натуральной системы координат.
на ось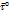 
:
Изменение скорости вдоль траектории произойдет, если будет изменяться вдоль траектории давление.
на ось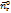 
:
на ось 
:
Последнее уравнение мы можем упростить, отбросив 
, 
, которые очень малы по сравнению с 
. От третьей проекции остается уравнение статики
Можно сделать вывод, что каков бы ни был горизонтальный ветер, распределение давления по вертикали будет такое же, как в случае покоя.
Умножим первое уравнение (проекцию 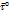на ) на 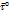, а второе (проекцию 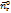на ) на 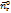и сложим, получим проекции уравнения движения на оси натуральной системы координат.
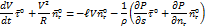
- полная горизонтальная производная, т. е. горизонтальное ускорение.
Рассмотрим, что такое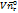 
?
|
|
|
Раскроем векторное произведение 
Следовательно, 
Введем понятие горизонтального градиента давления
Запишем уравнение горизонтального движения в натуральных координатах.
|
|
|
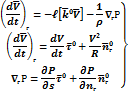
