 |
11. Высота обращения ветра. 12. Определение термического ветра на карте относительной топографии. 13. Градиентный ветер.
|
|
|
|
11. Высота обращения ветра.
Z обр – высота, при которой ветер поворачивает на 180º. (см. формулу в 10 вопр. «Случай №2»)
12. Определение термического ветра на карте относительной топографии.
Вспомним формулу для расчета относительного геопотенциала:
Нотн = Н2 – Н1 – толщина слоя между изобарическими поверхностями Р1 и Р2.
Обозначим постоянные 
через а1-2.
Нотн = Н2 – Н1 = а1-2Тср
Продифференцируем последнее уравнение по x и y.
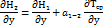
Умножим обе части уравнения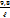 
и вспомним, что 
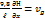, а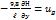 
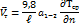
Формула для расчета скорости термического ветра на карте относительной топографии (ОТ) по внешнему виду такая же, как и формула для расчета геострофической скорости на карте абсолютной топографии (АТ), только в формуле 
- градиент относительного геопотенциала.
А барический закон выполняется и для термического ветра: термический ветер, направлен вдоль изотерм (или изогипс карты ОТ), так что область повышенных температур (относительного геопотенциала) остается справа.
13. Градиентный ветер.
Понятие геострофического ветра очень удобно, т. к. дает возможность по градиенту давления определить главную составляющую ветра. Но для анализа движения частицы атмосферы по криволинейным траекториям на карте геострофический ветер не очень удобен, так как он направлен по прямолинейным траекториям. Поэтому введено понятие градиентного ветра (Vgr), а геострофический ветер является частным случаем градиентного, когда изобары, выпрямляются.
Вспомним основное уравнение горизонтального движения в натуральных координатах из системы:
Градиентным ветром называется ветер, дующий с постоянной скоростью вдоль траектории.
|
|
|
Проекция уравнения движения на ось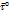 
:
При градиентном движении 
значит и 
, т. е. вдоль траектории давление не меняется. Значит градиентный ветер дует вдоль изобары и
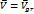
Уравнение градиентного движения запишется с учетом уравнений системы (3). Т. к. , то от ускорения останется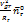 
, а т. к. , то от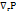 
останется 
.
Получим уравнение (1).
Решим это уравнение относительно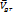 
.
Умножим векторно на 
.
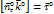
По правилу векторного произведения: если смотреть с конца 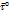, то переход от 
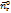к происходит против часовой стрелки.
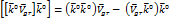
, т. к. 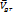перпендикулярно . 
.
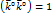Поэтому
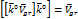
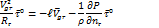
Таким образом, мы получили, что градиентный ветер направлен по касательной к траектории (изобаре) 
.
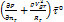– величина всегда положительная и на знак не влияет.
Значит на знак влияет только барический градиент 
.
В частном случае градиентный ветер переходит в геострофический, когда движение будет вдоль прямолинейных изобар. Тогда второй член скобки уравнения (! ) пропадает и остается:
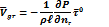
Если траектория движения криволинейная или замкнутая, то кроме сил барического градиента и Кориолиса появляется центробежная сила. При равномерном движении по криволинейной или круговой траектории эти три силы должны уравновеситься.
14. Равновесие сил в циклоне. Циклострофический ветер в циклоне.
Сила барического градиента 
направлена в сторону пониженного давления, т. е. к центру циклона. Центробежная сила 
всегда направлена от центра, и она меньше силы барического градиента.
Одна она уравновесить силу барического градиента не может, поэтому сила Кориолиса направлена противоположно силе барического градиента и примерно одного порядка с ней, поэтому может ее уравновесить. Сила Кориолиса направлена под углом 90º вправо от направления движения. Поэтому движение в циклоне должно быть против часовой стрелки. Таким образом, сумма сил центробежной и Кориолиса уравновешивает силу барического градиента.
|
|
|
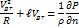
Решим квадратное уравнение
Перед корнем надо выбрать знак. Если 
, то 
, а это будет, когда скобка обращается в нуль. Значит перед корнем нужно оставить знак минус. Тогда:
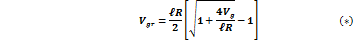
Формула (*) – для расчета скорости градиентного ветра при циклонической кривизне траектории.
|
|
|
