 |
15. Равновесие сил в антициклоне. Циклострофический ветер в АЦ.
|
|
|
|
15. Равновесие сил в антициклоне. Циклострофический ветер в АЦ.
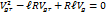
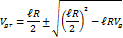
При 
, то 
Перед корнем должен стоять знак минус. Тогда:
Формулы для циклона и антициклона следующим образом:
(циклон Zn) 
(антициклон Az)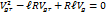
(циклон) 
(1)
(антициклон)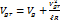 
(2)
Из формул (1) и (2) видно, что циклоническая кривизна уменьшает скорость ветра, по сравнению с геострофической, а антициклоническая – увеличивает.
В формуле для антициклона под корнем стоит разность. Поэтому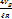 
не может быть больше единицы, т. к. в противном случае будут мнимые корни, которые физического смысла не имеют. Поэтому в антициклоне
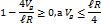
Значит, геострофический ветер и градиент давления не могут быть какими угодно, а зависят от размеров антициклона. Из формулы следует, что существует максимальное значение скорости градиентного ветра в антициклоне больше которого она на данной широте и на данном расстоянии от центра кривизны быть не может.
В циклоне же величина градиента давления, а значит, скорость ветра теоретически могут быть сколь угодно большими. Никаких ограничений на эти величины не налагается. Таким образом, циклоны в атмосфере могут быть сколь угодно глубокими, в то время как интенсивность антициклонов ограничена.
16. Геострофическая адвекция на высоте.
Адвекция – это горизонтальный перенос любого метеорологического свойства.
Мы хотим предсказать изменение температуры в данной точке. Для этого запишем полную производную по времени от температуры по оператору Эйлера.
|
|
|
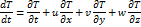
Изменение температуры в данной точке 
происходит за счет изменения температуры внутри частицы 
и за счет адвекции. Обычно предполагают, что для краткосрочных прогнозов можно считать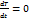 
, т. е. частица переходит с места на место, не меняя своей температуры. Это предположение близко к истине, т. к. радиационное изменение температуры внутри частицы происходит очень медленно. Тогда:
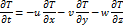
Так как основной перенос происходит только в горизонтальном направлении, то главным направлением в данной точке является геострофический ветер. Поэтому мы можем заменить фактический ветер геострофическим:
; 
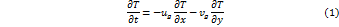
Это приращение температуры и носит название геострофической адвекции, т. е. приращения температуры за счет геострофического переноса.
Подставим в формулу (1) вместо 
и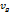 
их выражения через градиенты давления.
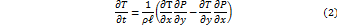
Скобка в уравнении (2) получила в метеорологической литературе название «адвективный фактор Погосяна-Таборовского», а в математике – это оператор Якоби (якобиан).
Свойства якобиана:
- перестановка аргументов в якобиане приведет к изменению знака:
- якобиан от одной и той же величины равен нулю: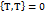 
В случае баротропной среды, когда плотность является функцией только давления или температуры, геострофическая адвекция не существует, т. к. в этом случае получится: 
.
Значит, адвекция температуры происходит только в бароклинной, т. е. реальной, атмосфере, когда 
.
Выразим якобиан через горизонтальные градиенты температуры и давления.
Составим векторное произведение градиентов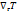 
и 
.
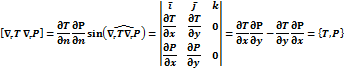
Значит, якобиан – это векторное произведение двух векторов градиентов.
Таким образом, запишем формулы для расчета геострофической адвекции.
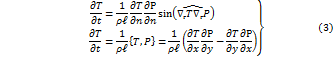
Угол, отсчитываемый против часовой стрелки – положительный, а по часовой стрелке – отрицательный.
На картах барической топографии формулы (3) использовать нельзя, т. к. на них наносятся абсолютные геопотенциальные высоты той или иной изобарической поверхности. Поэтому формулы для расчета геострофической адвекции на картах барической топографии можно получить, подставив в уравнение (1) проекции геострофической скорости в изобарической системе координат.
|
|
|
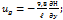
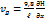
Обычно считается, что за период краткосрочного прогноза якобиан остается постоянным, поэтому уравнения (3) и (4) являются прогностическими.
|
|
|
