 |
9. Термический ветер. Тогда вектор термического ветра должен быть направлен по изотерме так, чтобы высокая температура оставалась справа.
|
|
|
|
9. Термический ветер.
Следовательно, вектор термического ветра является добавочным вектором и в сумме с вектором геострофического ветра на нижнем уровне образует вектор геострофического ветра на верхнем уровне.
Таким образом, изменение геострофического ветра с высотой происходит за счет изменения температуры 
и за счет добавочного термического ветра. До большой высоты множитель близок к единице. На уровне моря 
, на высоте 5 км 
, на высоте 11 км 
, то есть можно приравнять к единице в тропосфере.
Тогда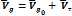 
Исследуем направление термического ветра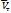 
по отношению к горизонтальному градиенту температуры 
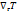. По формуле (31) 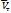пропорционален векторному произведению 
. По правилу векторного произведения вектор 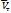направлен перпендикулярно плоскости векторов 
и 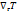и с конца его должен быть виден переход от векторов к 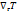против часовой стрелки.
Покажем это на рисунке 6: на горизонтальной плоскости проведем изотермы. Горизонтальный градиент температуры направлен в математике в сторону увеличения температуры, а вектор - вертикально вверх.
Тогда вектор термического ветра должен быть направлен по изотерме так, чтобы высокая температура оставалась справа.
Направление термического ветра
Следовательно, для термического ветра средний горизонтальный градиент температуры играет ту же роль, что и барический градиент для геострофического ветра.
Найдем компоненты 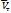в стандартных координатах.
- проекция на ось х
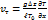– проекция на ось y
Модуль скорости термического вектора будет равен корню квадратному из суммы квадратов проекций.
Наличие угла между изобарами и изотермами приводит к перестройке термобарического поля. Так как геострофический ветер направлен по изобаре, то поворот геострофического ветра с высотой связан с поворотом изобар.
|
|
|
10. Четыре случая изменения геострофического ветра с высотой.
Рассмотрим влияние термобарического поля на изменение геострофического ветра с высотой.
Ранее было:
Найдем модуль геострофической скорости 
. Для этого уравнение возведем в квадрат.
Скалярное произведение 
.
Обозначим угол между векторам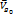и 
и 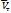через a. Покажем это на рисунке:
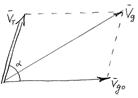
Угол между векторам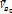и 
и 
Таким образом, значение ветра на высоте зависит и от угла a между изобарой и изотермой. Рассмотрим некоторые закономерности изменения геострофического ветра с высотой. Будем считать горизонтальный градиент температуры не меняющийся с высотой.
Проанализируем четыре характерных случая изменения геострофического ветра с высотой.
1) В первом случае барический и термический градиенты совпадают по направлению, а значит изобары и изотермы параллельны.
Ð a = 0 cosa = 1
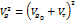
Геострофический ветер на нижнем уровне и термический ветер в слое направлены в одну сторону и алгебраически складываются. Это значит, что при совпадении направления градиентов температуры и давления ветер с высотой усиливается, не меняя своего направления.
2) 
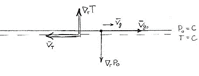Во втором случае градиент температуры направлен противоположно градиенту давления, т. е. изобары и изотермы антипараллельны.
Ð a = 180º; cosa = -1
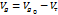
Рассмотрим изменение ветра с высотой на рисунке:
Изменение ветра с высотой
Из рисунка видно, что в случае, когда градиенты давления и температуры направлены противоположно друг другу, геострофический ветер с высотой ослабевает, на некоторой высоте обращается в нуль, а затем принимает противоположное направление, постепенно усиливаясь с высотой, если первоначальное условие относительного расположения векторов 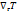и 
сохраняется на всех рассматриваемых высотах. Таким образом, ветер как бы поворачивает на 180º, т. е. происходит обращение ветра.
|
|
|
Если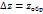 
, то 
и
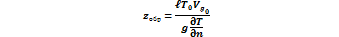
3) В третьем случае градиент температуры направлен вправо от градиента давления. Следовательно, область более высоких температур располагается в направлении, противоположном направлению ветра. В результате в т. М с течением времени будут приходить частицы с все более высокой температурой, т. е. этот случай соответствует адвекции тепла.
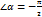, т. к. угол отсчитывается по часовой стрелке от 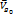к 
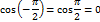
Значение скорости ветра на верхнем уровне может быть найдено по теореме Пифагора. Из рисунка видно, что ветер с высотой повернул вправо.
Таким образом, в слое адвекции тепла геострофический ветер поворачивает с высотой вправо.
4) В четвертом случае градиент температуры направлен влево от градиента давления, что соответствует расположению области более низких температур в направлении, противоположном направлению ветра. В результате в т. М с течением времени будут приходить частицы с все более низкой температурой, то есть имеет место адвекция холода.
; 
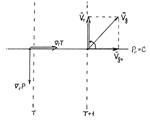
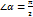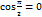Ð a > 0, т. к. от 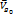к отсчитывается против часовой стрелки
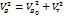
Так же, как и в случае (3) квадрат гипотенузы равен сумме квадратов катетов. Видно, что ветер с высотой повернул влево.
Таким образом, в слое адвекции холода геострофический ветер поворачивает с высотой влево .
|
|
|
