 |
4. Основное уравнение движения в сферических координатах.
|
|
|
|
4. Основное уравнение движения в сферических координатах.
Уравнения написаны при допущении, что влиянием на атмосферные движения кривизны земной поверхности можно пренебречь. Такое допущение справедливо во всех случаях, за исключением того, когда рассматривается задача об общей циркуляции атмосферы.
В этом случае масштаб рассматриваемого движения сравним с масштабом земного шара и поэтому уравнения необходимо заменить соответствующими уравнениями в сферических координатах. Запишем проекции уравнения движения в сферической системе координат.
Положение точки В определяется тремя сферическими координатами: r, j, l.
Между сферическими и стандартными координатами есть связь.
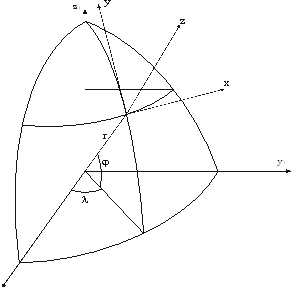
Сферическая система координат
Теперь можно преобразовать уравнения из стандартной в сферическую систему координат:
Строго говоря, все прогностические схемы следовало бы рассматривать в сферической системе. Но эта система очень сложна, поэтому уравнения в этой системе применяются для долгосрочных прогнозов погоды, так как за большие промежутки времени частица огибает большие дуги. А при краткосрочном прогнозе Землю можно считать плоской и использовать уравнения в стандартных координатах.
5. Геострофическое движение.
Если нормальная и тангенциальная компоненты ускорения равны нулю, то горизонтальное движение без трения называется геострофическим.
Если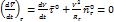 
, то 
– геострофический ветер.
Условие требует, чтобы обе проекции по отдельности равнялись нулю.
Проекция уравнения на ось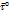 
натуральной системы координат выглядит так:
|
|
|
По условию геострофического движения проекция 
на ось 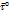равна 0, значит 
, т. е. геострофический ветер направлен вдоль изобары и траектория движения является изобарой.
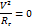
Это равенство осуществляется тогда, когда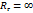 
. На карте это прямая линия. Значит при геострофическом движении траектория является прямой линией. В системе было:
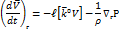
При геострофическом движении ускорение равно нулю. Тогда получим
Из этого уравнения желательно получить вектор геострофической скорости. Для этого умножим векторно обе части уравнения на 
.
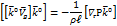
Раскроем двойное векторное произведение
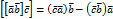
У нас получится:
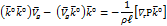
Скалярное произведение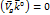 
, т. к. 
находится в горизонтальной плоскости, – в вертикальной и скалярное произведение взаимно перпендикулярных векторов равно нулю: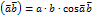 
. Скалярное произведение коллинеарных векторов равно единице: 
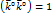. Тогда наше уравнение примет вид:
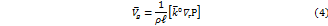
Минуса перед правой частью нет, т. к. мы поменяли местами векторы в векторном произведении 
.
Полный градиент давления 
состоит из градиента вертикального и горизонтального: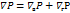 
.
Горизонтальный градиент давления приблизительно в 2500 раз меньше, чем вертикальная составляющая.
Составим векторное произведение 
:
, т. к.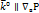 
Следовательно: 
Тогда скорость геострофического ветра запишется так:
Таким образом, прямолинейное равномерное движение воздуха в горизонтальной плоскости под действием силы барического градиента и силы Кориолиса при отсутствии силы трения называется геострофическим ветром.
6. Геострофический ветер в стандартной системе координат.
Найдем проекции геострофической скорости на оси стандартной системы координат:
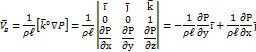
Уравнение позволяет рассчитать модуль геострофической скорости.
Вспомним проекции уравнения движения на оси x и y стандартной системы координат. Для свободной атмосферы (без учета трения) первые два уравнения будут выглядеть так:
|
|
|
Из этих уравнений видно, что геострофический ветер имеет место при уравновешивании отклоняющей силы вращения Земли и силы барического градиента.
Легко увидеть, что направление геострофического ветра перпендикулярно направлению градиента давления. Это следует и из формулы.
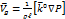– векторное произведение всегда перпендикулярно двум другим векторам и 
.
Кроме того, умножая первое уравнение системы на 
, второе на 
и складывая оба уравнения, имеем:
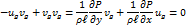
Если скалярное произведение векторов равно нулю, то эти векторы взаимно перпендикулярны.
Значит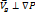 
.
Если бы не было разности давлений, то есть силы барического градиента, то не возникло бы движение частиц воздуха. Но как только под влиянием каких-то причин (например, местного нагрева или охлаждения подстилающей поверхности) возникла разность давлений, частица из точки А начинает движение в сторону низкого давления.
Движение частицы из т. А в сторону низкого давления
Если бы Земля не вращалась, то движение происходило бы всегда от большего давления к меньшему. Но с появлением и увеличением скорости движения одновременно начинает действовать все возрастающая отклоняющая сила вращения Земли. Под ее влиянием возникающий ветер будет все больше и больше отклоняться от направления силы барического градиента в северном полушарии вправо, а в южном – влево. Наконец, ветер отклонится от силы градиента на прямой угол, при котором силы барического градиента и отклоняющая направлены противоположно друг другу.
В таком положении сила барического градиента уже не может вызвать увеличение скорости, поэтому возрастание скорости ветра прекратится. При равенстве сил барического градиента и отклоняющей силы вращения Земли ветер приобретает устойчивое направление и постоянную скорость, то есть движение становится установившимся, а ветер геострофическим, направленным вдоль траектории (изобары), так что высокое давление остается справа (в северном полушарии).
Таким образом, мы можем сформулировать барический закон ветра:
|
|
|
