 |
Данные своего варианта принять по таблице 4 , рисунок 4
|
|
|
|
Данные своего варианта принять по таблице 4, рисунок 4
Таблица 4
| номер варианта | F1, kH | F2, kH | A1, см2 | A2, см2 | |||||||||
| 5, 6 | 9, 2 | 0, 4 | 0, 6 | ||||||||||
| 1, 2 | 3, 6 | 0, 5 | 1, 9 | ||||||||||
| 2, 4 | 6, 5 | 1, 2 | 3, 2 | ||||||||||
| 0, 9 | 2, 4 | ||||||||||||
| 1, 4 | 3, 8 | 0, 7 | 1, 2 | ||||||||||
| номер схемы на рисунке 4 | - | - | - | - | |||||||||
| - | - | - | - | ||||||||||
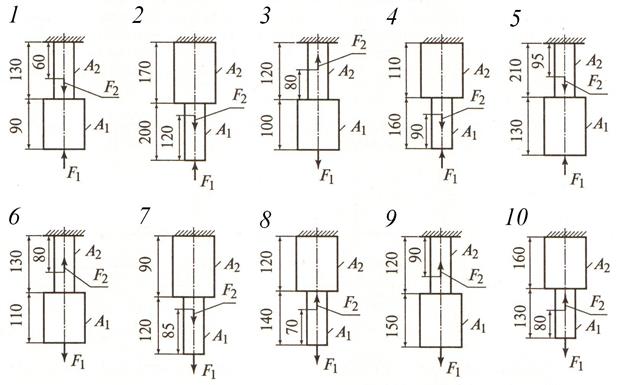
Рисунок 4
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению контрольной работы № 1
В рекомендованных учебниках, а также в руководствах и интернет ресурсах обучающиеся найдут достаточное число примеров задач, подобных тем, которые включены в контрольную работу, поэтому ниже даны лишь необходимые краткие методические указания к решению задач контрольной работы.
Задачи №№ 1-10 следует решать после изучения тем 1. 1 - 1. 2 раздела «Теоретическая механика». В задачах рассматривается равновесие плоской системы сходящихся сил и требуется определить равнодействующую системы си.
Последовательность решения задач №№ 1-10
1. Указывают точку, равновесие которой рассматривается
В задачах такой точкой является центр тяжести тела или точки пересечения всех стержней и нитей.
2. Прикладывают к рассматриваемой точке активные силы
Активными силами являются собственный вес тела или вес груза, которые направлены к центру тяжести земли. При наличии блока вес груза действует на рассматриваемую точку вдоль нити. Направление действия этой силы устанавливается из чертежа. Вес тела принято обозначать G
3. Мысленно отбрасывают связи, заменяя их действия реакциями связей
|
|
|
При замене связей реакциями следует помнить, что реакция плоскости направлена по нормали (перпендикуляру)к ней в точке контакта, а реакции стержня и нити – по их осям. Реакцию нити и стержня принято называть усилиями.
1. Выбираем положение прямоугольной системы координат
Начало координат совмещают с точкой, равновесие которой рассматривается.
5. Составляют уравнения равновесия вида: Σ Fx= 0; Σ Fу = 0
Напомним! если в результате решения искомая реакция получается положительной, то это значит, что направление ее выбрано верно, если отрицательной, то направление реакции необходимо заменить на противоположное (модуль ее при этом остается прежним).
6. Выполняем проверку решения графическим или геометрическим способом.
7. Определяем равнодействующую силу Численное значение равнодействующей силы 
через ее проекции определяется по формуле
Направление определим по косинусам углов, которые эта сила образует с координатными осями:
Пример 1.
Фонарь весом 80 Н подвешен на кронштейне АВС, укреплённом на вертикальной стене (рис. 2-а). Определить усилия возникшие в горизонтальном стержне СВ и наклонной тяге АВ после подвески фонаря, если СВ=1м и АВ= 1, 2м. Соединения в точках А, В и С – шарнирные.
|
Дано: АВ-1, 2м
СВ=1 м
G=80Н
Определить: RA, RB.
 |
1 Рассматриваем равновесие шарнира В.
|
|
|
2 Освобождаем шарнир В от связей и изображаем
действующие на него активные силы и реакции связей (рис. 2-б).
2-б У 3 Выбираем систему координат и составляем уравнение
RA для системы сил, действующих на шарнир В
α β Σ F Х = 0 - RА cos α – RС = 0 (1)
RС Х Σ F У = 0 RА cos β - G = 0 (2)
G
4. Определяем реакции стержней, решая уравнения (1) и (2).
Из уравнения (2): RА = G / cos β
По теореме Пифагора находим АС: АС = √ АВ2 –ВС2 = √ 1, 22 –12 = 0, 664 м.
cos β = 0, 664 / 1, 2, тогда RА = ( 80 · 1, 2) / 0, 664 = 144, 5 Н
Из уравнения (1): - RС = RА cos α ; RС = 144, 5 · (1/ 1, 2) = - 120, 5 Н
Знак минус перед значением RС указывает на то, что направление реакции в
противоположную сторону, т. е. к шарниру В. (деформация сжатия)
5. Правильность полученных результатов можно проверить, решая задачуграфически.
Для решения задачи графическим способом выбирают масштаб (например 1: 20) и строят кронштейн АВС. Для чего из произвольной точки С (рис. 2-в) проводим горизонтальную и вертикальную линии. На горизонтальной линии отложим отрезок СВ= (1м=1000мм/20)=50 мм. При помощи циркуля из точки В отложим отрезок АВ=60 мм. Построенный треугольник АВС изображает в масштабе данный в условии задачи кронштейн. (2-в)
|
а
отрезком ВД=20 мм.
 |
Значит масштаб построения для сил:
М = G / ВД = 80 Н / 20 мм = 4 Н/мм ( 4 Н в 1 мм ).
|
|
|
Благодаря тому, что в точках А, В и С кронштейна соединения шарнирные, стержни, находясь под действием веса фонаря, либо сжимаются, либо растягиваются. Иными словами, искомые усилия действуют вдоль стержней.
Изобразим направление действия искомых сил линиями Аа и Сс, пересекающимися в точке В – точка приложения к кронштейну веса фонаря. Из точки Д (конца вектора G ) проводим прямые ДМ параллельно Аа. В получившемся параллелограмме ВМДL стороны ВМ и ВL изображают силы RА и RС , действующие соответственно на тягу АВ и стержень ВС. При помощи масштабной линейки измерим отрезки ВМ и ВL: ВМ = 36 мм, ВL = 30 мм
Следовательно: RА = МF · ВМ = 4 Н/ мм · 36 мм = 144 Н
RС = МF · В L = 4 Н/ мм · 30 мм = 120 Н
Графическое решение подтверждает правильность аналитического решения.
Ответ: RА = 144 Н, RС = 120 Н.
Определяем равнодействующую силу Численное значение равнодействующей силы через ее проекции определяется по формуле
Задачи №№ 11-20; следует решать после изучения тем 1. 1 - 1. 2. раздела «Теоретическая механика». В задачах требуется определить реакции в опорах балок Обучающимся необходимо уметь определять реакции опор, так как с этого начинается решение многих задач по сопротивлению материалов и деталям машин.
|
|
|
