 |
Последовательность решения задач №№ 11-20;
|
|
|
|
Последовательность решения задач №№ 11-20;
1. Заменяют распределённую нагрузку её равнодействующей
Для равномерно распределённой нагрузки равнодействующая равна произведению интенсивности нагрузки g на длину участка ℓ , на котором она действует G = gℓ
Перед решением задач рекомендуется уяснить и закрепить порядок нахождения равнодействующей и определения расстояний от неё до опор. При отсутствии навыков решения таких задач необходимо указывать положение равнодействующей относительно опор.
2. Обозначают опоры
Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно – неподвижную и вторую шарнирно –подвижную опору.
3. Освобождают от опор и заменяют их действие на балку реакциями.
В задачах на балку действуют только вертикальные нагрузки и сосредоточенные моменты. Реакции опор при нагрузке будут только вертикальными. Обычно их направляют вверх (против действия основной нагрузки) и обозначают реакцию опор
А - RА, В – RВ
4. Составляют уравнения равновесия вида: Σ МА = 0, Σ МВ = 0
Напомним, что моментом силы относительно точки называется произведение этой силы на плечо – кратчайшее расстояние от этой точки приложения силы (в общем случае до линии действия силы).
Если сила стремится повернуть балку относительно рассматриваемой точки по часовой стрелке, то будем считать её момент положительным, а если против – отрицательным.
Сосредоточенный момент не умножается на расстояние до опоры, а правило знаков остаётся тем же, что для момента силы.
5. Выполняют проверку решения: Для этого составляют уравнение равновесия:
Σ Fy= 0
|
|
|
Пример 2
Определить реакции: 
, 
и 
.
Направления реакций выбираем произвольно. Направим обе вертикальные реакции вверх, а горизонтальную реакцию – влево.
Для вычисления значений реакций опор составим уравнения статики:
Сумма проекций всех сил (активных и реактивных) на ось z равна нулю: 
.
Поскольку на балку действуют только вертикальные нагрузки (перпендикулярные к оси балки), то из этого уравнения находим: горизонтальная реакция неподвижной шарнирной опоры 
.
Сумма моментов всех сил относительно опоры А равна нулю: 
.
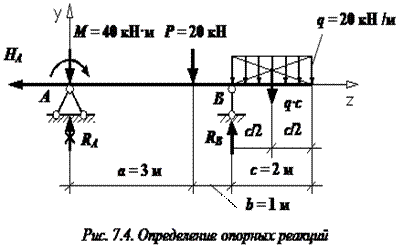
Правило знаков для момента силы: считаем момент силы положительным, если он вращает балку относительно точки по ходу часовой стрелки.
Необходимо найти равнодействующую равномерно – распределенной погонной) нагрузки. Распределенная погонная нагрузка равна площади эпюры распределенной нагрузки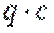 
и приложена в центре тяжести этой эпюры (посредине
участка длиной 
), тогда
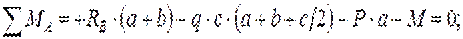
кН.
Сумма моментов всех сил относительно опоры B равна нулю: .
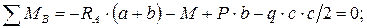
кН.
Знак «минус» в результате говорит: предварительное направление опорной реакции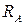 
было выбрано неверно. Меняем направление этой опорной реакции на противоположное (см. рис. 7. 4) и про знак «минус» забываем.
Проверка опорных реакций
Сумма проекций всех сил на ось y должна быть равна нулю: .
Силы, направление которых совпадает с положительным направлением оси y, проектируются на нее со знаком «плюс»:
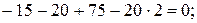
(верно).
Задачи №№ 21-30 следует решать после изучения темы1, 3. Центр тяжсти.
Основные формулы и предпосылки:
Центры тяжести простейших сечений (рис. 3-а)
рис. 3 - а
|
Геометрические характеристики стандартных прокатных профилей (Приложение 1)
|
|
|
Методы расчёта: - метод симметрии;
- метод разделение на простые части
- метод отрицательных площадей
Координаты центра тяжести сложных и составных сечений:
Хс = ∑ Аk • Xk / A; Yс = ∑ Аk • Yk / A;
Аk -площади частей сечения,
Xk , Yk - координаты ЦТ частей сечения,
А – суммарная площадь сечения: А = ∑ Аk
|
|
|
