 |
1.2. Формулы алгебры логики. 1.3. Приложение алгебры логики. Релейно-контактые схемы
|
|
|
|
1. 2. Формулы алгебры логики
Формулами алгебры логики называются выражения, полученные из переменных x, y, … посредством применения логических операций: отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, а также сами переменные, принимающие значения истинности высказываний x, y, ….
Формулы алгебры логики будем обозначать большими буквами латинского алфавита: А, В, …..
Если в формулу алгебры логики вместо переменных x, y, … подставить конкретные высказывания, то получится высказывание, имеющее логическое значение «1» или «0».
Пример.
Высказывание x: «Волга впадает в Каспийское море» – истинное (x = 1),
высказывание y: «Число 16 кратно 3» – ложное (y = 0),
тогда формула А = x Ú y будет иметь логическое значение «1»: А = 1 (см. таблицу истинности для х Ú y).
На основе таблиц истинности основных логических операций можно составлять таблицы истинности для различных формул алгебры логики.
Две формулы алгебры логики называются равносильными или эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы переменных (элементарных высказываний). Равносильность формул А и В будем обозначать знаком «º »: А º В.
Равносильность логических формул можно установить при помощи их таблиц истинности.
Пример. С помощью таблиц истинности проверить, являются ли равносильными формулы А = 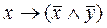 и В =
и В = 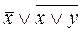 .
.
Решение. Составим таблицы истинности для каждой из формул А и В.
| x | y | 
| 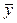
|  Ù Ù 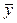
| А = 
|
| x | y | 
| x Ú y | 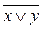
| В = 
|
Ответ: данные формулы являются равносильными.
|
|
|
Другой способ доказательства равносильности логических формул – их упрощение с использованием основных равносильностей.
Основные равносильности.
Для любых элементарных высказываний x, y, z справедливы следующие равносильности, которые можно разбить на 3 группы.
1. Основные законы:
1) x Ù x º x; 2) x Ú x º x; 3)  º x;
º x;
4) x Ù 0 º 0; 5) x Ú 0 º x; 6)  Ù x º 0;
Ù x º 0;
7) x Ù 1 º x; 8) x Ú 1 º 1; 9)  Ú x º 1;
Ú x º 1;
законы поглощения:
10) x Ù (y Ú x) º x; 11) x Ú (y Ù x) º x.
2. Выражения одних логических операций через другие:
12) x ® y º  Ú y; 13)
Ú y; 13)  ;
;
14) x « y º (x ® y) Ù (y ® x); 15)  .
.
3. Свойства логических операций:
16) x Ù y º y Ù x; 17) x Ú y º y Ú x;
18) x Ù (y Ù z) º (x Ù y) Ù z; 19) x Ú (y Ú z) º (x Ú y) Ú z;
20) x Ù (y Ú z) º (x Ù y) Ú (x Ù z); 21) x Ú (y Ù z) º (x Ú y) Ù (x Ú z).
Множество высказываний с введенными для них логическими операциями и основными равносильностями называется алгеброй Буля.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквиваленция. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
Пример. Упростить логическую формулу:  .
.
Решение. Используем основные равносильности.

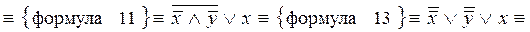
 .
.
Ответ: А º x Ú y.
1. 3. Приложение алгебры логики. Релейно-контактые схемы
Релейно-контактной схемой (РКС) или переключательной схемой называется схематическое изображение устройства, состоящего из следующих элементов:
1) переключателей (контактов, реле, ламп и др. );
|
|
|
2) соединительных проводников;
3) входов-выходов (полюсов РКС).
Рассмотрим простейшую РКС, содержащую один переключатель Р. Если переключателю Р поставить в соответствие высказывание х: «Переключатель Р замкнут», то истинному значению х (х = 1) будет соответствовать замкнутое состояние переключателя, при котором РКС проводит ток, т. е. импульс, поступающий на вход, может быть снят на выходе. Значению х = 0 будет соответствовать разомкнутое состояние РКС (ток не проводится).
Каждой РКС, состоящей из нескольких переключателей, можно поставить в соответствие высказывание, выраженное некоторой формулой А, таким образом, что истинному значению формулы (А = 1) будет соответствовать замкнутое состояние РКС, а значению А = 0 – разомкнутое состояние. Примеры таких соответствий приведены в таблице.
Простейшие РКС и соответствующие им формулы логики.
| РКС | Формула | Значения |
Переключатель х:
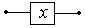
| Простейшее высказывание: х | х = 1, если переключатель замкнут; х = 0, если переключатель разомкнут |
Переключатель 
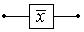
| Отрицание простейшего высказывания: 
|  = 0, если переключатель замкнут; = 0, если переключатель замкнут;
 = 1, если переключатель разомкнут = 1, если переключатель разомкнут
|
Последовательное соединение:
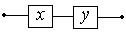 (схема замкнута, когда
оба переключателя замкнуты)
(схема замкнута, когда
оба переключателя замкнуты)
| Конъюнкция высказываний: x Ù y | 
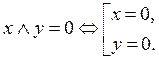
|
Параллельное соединение:
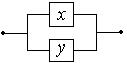 (схема разомкнута, когда
оба переключателя разомкнуты)
(схема разомкнута, когда
оба переключателя разомкнуты)
| Дизъюнкция высказываний: x Ú y | 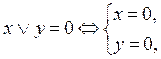
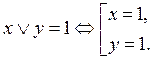
|
Схема, которая всегда разомкнута

| x Ù 
| x Ù  º 0 º 0
|
Схема, которая всегда замкнута

| x Ú 
| x Ú  º 1 º 1
|
Из простейших РКС путем их последовательного и параллельного соединения могут быть построены более сложные переключательные схемы.
Доказано, что любая формула алгебры логики может быть преобразована к виду, содержащему только операции отрицания, конъюнкции и дизъюнкции. Это позволяет изображать логические формулы при помощи РКС, а РКС задавать формулами.
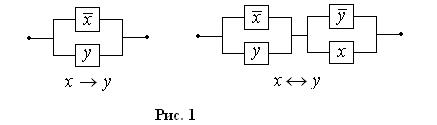
Например, согласно формулам основных равносильностей
x ® y º  Ú y и x « y º (x ® y) Ù (y ® x),
Ú y и x « y º (x ® y) Ù (y ® x),
следовательно, логическим операциям импликации и эквиваленции соответствуют РКС, изображенные рис. 1.
 Используя равносильные преобразования логической формулы, соответствующей некоторой РКС, можно упростить РКС, т. е. привести ее к виду, содержащему меньшее число переключателей.
Используя равносильные преобразования логической формулы, соответствующей некоторой РКС, можно упростить РКС, т. е. привести ее к виду, содержащему меньшее число переключателей.
|
|
|
 Пример. Упростить РКС, изображенную на рис. 2.
Пример. Упростить РКС, изображенную на рис. 2.
Решение. Запишем соответствующую РКС формулу, используя таблицу простейших РКС и соответствующих им формул логики:
 .
.
Упростим формулу, используя основные равносильности:
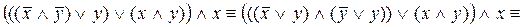
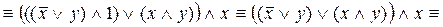
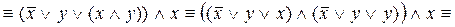
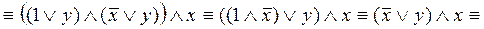

 .
.
Таким образом,  . Построим РКС, соответствующую упрощенной формуле (рис. 3).
. Построим РКС, соответствующую упрощенной формуле (рис. 3).
|
|
|


