4.2. Экстремумы функционала

Функционал I [y (x)], определенный на некотором пространстве функций (кривых) достигает на кривой y = y₀(x) экстремума, если существует 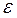-окрестность этой кривой, в которой приращение функционала сохраняет знак, причем, если DI = I [y] – I [y₀] > 0, то функционал I [y] достигает на кривой y = y₀(x)  минимума, а если DI < 0, то функционал I [y] достигает на кривой y = y₀(x) максимума. Функцию y₀(x) называют соответственно точкой минимума  или  точкой максимума.

Теорема. (Необходимое условие локального экстремума).

Если функционал I [y (x)], имеющий вариацию, достигает минимума или максимума на кривой y = y₀(x), где y₀(x) – внутренняя точка области определения функционала, то при y(х)= y₀(x) вариация функционала равна нулю:

d I [y₀(x)] = 0.                                          (3)

Функции, удовлетворяющие условию (3), называются экстремалями функционала.

Вариационная задача: среди функций (кривых) y (x), принадлежащих некоторому множеству М, требуется найти кривую y = y*(x), на которой функционал I [y (x)], определенный на множестве М, достигает экстремума, т. е. .

Решение этой задачи заключается в поиске экстремалей, т. е. функций, «подозрительных на экстремум», и в последующей проверке выполнения достаточных условий существования экстремума. На практике, как правило, экстремалей немного, и установить наличие (или отсутствие) на них экстремума функционала удается, исходя из смысла задачи. Следует отметить, что вариационная задача не всегда имеет точное решение, а если решение существует, то оно не всегда единственно.

Рассмотрим пространство M функций y (x), дифференцируемых на отрезке [a; b] и удовлетворяющих граничным условиям:

y(a) = A, y(b) = B,                                           (4)

то есть все кривые проходят через две закрепленные граничные точки.

Пусть на этом пространстве M определен функционал

I [y (x)] = 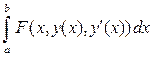,                    (5)

где подынтегральная функция 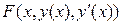 имеет непрерывные частные производные до второго порядка включительно по всем переменным.

Требуется найти экстремали функционала I [y (x)].

Можно доказать, что, если для функционала (5) выполнено необходимое условие (3), то функция 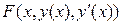 удовлетворяет уравнению Эйлера:

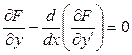                          (6)

Так как  тоже является функцией от , то это уравнение можно записать в развернутой форме:

.               (7)

При   уравнение Эйлера  представляет собой обыкновенное дифференциальное уравнение второго порядка относительно функции y (x). Его общее решение зависит от двух произвольных постоянных С₁, С₂, которые можно найти из граничных условий (4).

Пример. Найти экстремали функционала , удовлетворяющие граничным условиям y(0) = 0, y(ln2) = 2.

Решение. Запишем уравнение Эйлера (7) для данного функционала. Для подынтегральной функции , получаем частные производные

, .

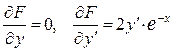Тогда уравнение Эйлера:  или 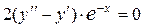. Учитывая, что 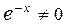, получаем  – однородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно функции y (x).

Его характеристическое уравнение k² – k = 0 имеет корни k₁ = 0, k₂ = 1.

Напомним, что общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами в зависимости от корней характеристического уравнения имеет вид:

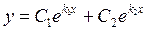, если  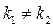 (корни вещественные различные);

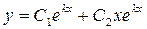, если  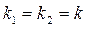(корни вещественные равные);

, если  (корни комплексно-сопряженные).

В данном случае k₁ = 0, k₂ = 1, 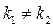и общее решение уравнения имеет вид .

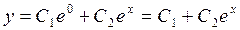Определим произвольные постоянные С₁, С₂ из граничных условий

Отсюда получаем С₁ = –2, С₂ = 2, следовательно,  экстремаль функционала .

Ответ. .

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: