 |
5. Оптимальное управление. 5.1. Математическая модель системы управления. 5.2. Оптимальное управление динамической системой
|
|
|
|
5. Оптимальное управление
5. 1. Математическая модель системы управления
Система управления состоит из управляющего устройства (УУ) и объекта управления (ОУ). Примерами систем управления служат семейный бюджет, экономика отрасли, технологический процесс, научное исследование и т. д.
УУ передает в ОУ сигнал – управление. Управление может быть механическим воздействием, электромагнитным импульсом, потоком инвестиций и др. Под воздействием сигнала u (t), где t – время, u (t) – скалярная или векторная функция, система изменяет свое состояние (возможна обратная связь). Простейшая математическая модель системы управления без учета внешних воздействий включает:
• модель ОУ – оператор, в соответствии с которым осуществляется преобразование входа – управления u (t) в реакцию системы;
• алгоритм управления, который зависит от цели управления и наличия обратной связи.
В общем случае состояние динамической системы управления характеризуется n-мерным вектором (матрицей-столбцом)
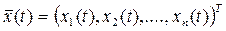 ,
,
где xj (t) для j = 1, 2, …, n называют фазовыми координатами, а  – фазовым вектором.
– фазовым вектором.
Например, положение самолета определяет 6-мерный вектор, в котором 3 координаты задают положение центра масс самолета в пространстве и 3 координаты – его вращение относительно центра масс. Курс самолета – это вектор-функция 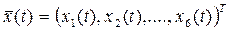 .
.
Модель ОУ обычно описывается уравнениями состояний, отражающих законы физики, экономики и прочее. Довольно часто процесс управления без учета внешних воздействий может быть задан системой обыкновенных дифференциальных уравнений:
 (8)
(8)
или, в векторной форме: 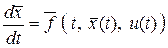 , где
, где 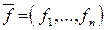 – вектор-функция, характеризующая изменение состояния системы, u (t) – функция управления. В реальных условиях множество управлений ограничено:
– вектор-функция, характеризующая изменение состояния системы, u (t) – функция управления. В реальных условиях множество управлений ограничено:  , где U – класс допустимых управлений.
, где U – класс допустимых управлений.
|
|
|
Для того, чтобы процесс управления был определен на некотором промежутке 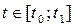 , необходимо задать начальное состояние системы – вектор
, необходимо задать начальное состояние системы – вектор  . Тогда
. Тогда 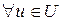 будет соответствовать траектория – вектор-функция
будет соответствовать траектория – вектор-функция  , переводящая систему из состояния
, переводящая систему из состояния  в
в 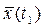 – состояние, достижимое из состояния
– состояние, достижимое из состояния  на данном классе управлений U.
на данном классе управлений U.
5. 2. Оптимальное управление динамической системой
Рассмотрим некоторый процесс управления без учета внешних воздействий, заданный системой обыкновенных дифференциальных уравнений  , где
, где  – заданная вектор-функция, u (t) – функция управления из некоторого класса допустимых управлений U, и
– заданная вектор-функция, u (t) – функция управления из некоторого класса допустимых управлений U, и 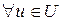 соответствует фазовый вектор
соответствует фазовый вектор  (траектория).
(траектория).
Если определена цель управления, то имеет смысл искать наилучшее (оптимальное) управление для достижения этой цели. В большинстве случаев цель управления можно задать в форме вариационной задачи – поиска экстремума некоторого функционала I [u (t)] на классе допустимых управлений U. Тогда задача оптимального управления: найти оптимальное управление u*(t) и соответствующую ему оптимальную траекторию  , для которых
, для которых
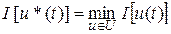 (другая форма записи:
(другая форма записи:  ),
),
или  (
( 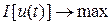 ).
).
Функционал I [u ] называется критерием качества управления. Например, в так называемой «задаче Лагранжа» роль критерия качества выполняет интегральный функционал вида
 (9)
(9)
где 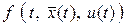 – заданная функция.
– заданная функция.
5. 3. Принцип максимума Понтрягина
Рассмотрим простейшую задачу управления: задана модель системы управления  , где
, где 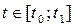 ,
,  – непрерывная вектор-функция,
– непрерывная вектор-функция,  – функция управления, и критерий качества управления
– функция управления, и критерий качества управления
 .
.
Пусть каждому управлению  соответствует траектория
соответствует траектория  , переводящая систему из состояния
, переводящая систему из состояния  в
в 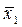 , где
, где  и
и 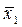 фиксированы.
фиксированы.
Требуется найти оптимальное управление u*(t) и соответствующую ему оптимальную траекторию  , для которых
, для которых 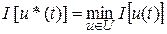 . Это задача Лагранжа с фиксированным временем и закрепленными концами траекторий:
. Это задача Лагранжа с фиксированным временем и закрепленными концами траекторий:  ,
,  .
.
|
|
|
Допустим, существует оптимальное управление 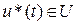 и соответствующая ему оптимальная траектория
и соответствующая ему оптимальная траектория  , удовлетворяющие условиям задачи.
, удовлетворяющие условиям задачи.
Введем вспомогательную вектор-функцию  , где
, где 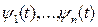 – неизвестные функции, кусочно-непрерывные на
– неизвестные функции, кусочно-непрерывные на 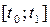 , и построим функцию Гамильтона-Понтрягина (гамильтониан):
, и построим функцию Гамильтона-Понтрягина (гамильтониан):

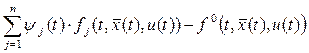 . (10)
. (10)
Очевидно, что  .
.
При фиксированных  гамильтониан является функцией управления. Можно доказать, что если u*(t) – оптимальное управление, то при u = u*(t) гамильтониан достигает максимума по управлению и выполняются условия
гамильтониан является функцией управления. Можно доказать, что если u*(t) – оптимальное управление, то при u = u*(t) гамильтониан достигает максимума по управлению и выполняются условия
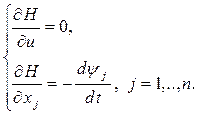
Принцип максимума Понтрягина.
Если 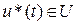 – оптимальное управление, переводящее систему из состояния
– оптимальное управление, переводящее систему из состояния  в
в 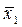 и
и  – соответствующая ему оптимальная траектория, которая в первый раз достигает точки
– соответствующая ему оптимальная траектория, которая в первый раз достигает точки 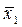 в момент t1, то
в момент t1, то
1) существует вектор 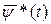 , соответствующий u*(t) и
, соответствующий u*(t) и  , причем
, причем 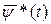 и
и  являются решениями системы дифференциальных уравнений
являются решениями системы дифференциальных уравнений
 (11)
(11)
удовлетворяющими условиям
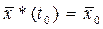 ,
,  ; (12)
; (12)
2) в каждой точке непрерывности функции u*(t) достигается максимум гамильтониана по управлению:
 . (13)
. (13)
Система (11) называется канонической системой задачи оптимального управления. Для получения ее частного решения (определения констант интегрирования) используют граничные условия (12).
Принцип максимума представляет собой необходимое условие оптимальности. Если получается несколько управлений, удовлетворяющих условиям (11)-(13), то проверяют выполнение достаточных условий, или выбирают одно из них, исходя из смысла задачи.
Идея принципа максимума: чтобы найти u*(t) – оптимальное управление, минимизирующее функционал I [u (t)], нужно найти управление, максимизирующее гамильтониан: 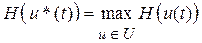 .
.
|
|
|


