 |
2. Булевы функции. 3.1. Основные определения
|
|
|
|
2. Булевы функции
Будем рассматривать логические переменные x1, x2, …, xn, принимающие только два значения: «1» или «0».
Булевой функцией f (x1, x2, …, xn) называется произвольная функция, аргументами которой являются логические переменные и принимающая только одно из двух значений: «1» или «0».
Количество булевых функций одного аргумента равно 22 = 4, это функции:
f1(x) = 0, f2(x) =1, f3 (x) = x и f4(x) = 
.
Булевых функций двух аргументов всего 24 = 16, а количество булевых функций n аргументов равно 
.
Всякой формуле алгебры логики, составленной из элементарных высказываний x1, x2, …, xn соответствует булева функция f (x1, x2, …, xn), аргументы которой принимают значения истинности соответствующих элементарных высказываний: «1» или «0». Две равносильные формулы алгебры логики определяют одну и ту же булеву функцию, т. к. значения истинности этих формул совпадают для одинаковых значений входящих в них переменных.
Для булевых функций можно составлять таблицы значений – всякую булеву функцию n аргументов можно задать таблицей из 2n строк.
Например, таблица значений некоторых функций 2-х аргументов, соответствующих основным логическим операциям (отрицание одного аргумента, конъюнкция, дизъюнкция, импликация и эквиваленция) выглядит так:
| x1 | x2 | 
| x1 Ù x2 | x1 Ú x2 | x1 ® x2 | x1 « x2 |
Значение булевой функции f (x1, x2) при известных значениях аргументов устанавливается по строке таблицы, соответствующей заданным значениям x1 и x2. Например, для функции f (x1, x2) = x1 ® x2 значение f (1, 0) = 0, а значение f (1, 1) = 1.
Каждой релейно-контактной схеме (РКС), составленной из переключателей x1, x2, …, xn, можно поставить в соответствие булеву функцию, называемую ее функцией проводимости:
|
|
|
Функция проводимости РКС задается при помощи формулы логики, соответствующей этой РКС. Например, РКС, изображенная на рис. 2, имеет функцию проводимости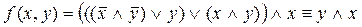 
, таблица значений которой имеет вид:
| х | y | f(x, y) |
3. Графы
3. 1. Основные определения
Рассмотрим некоторое конечное множество точек V = {v1, v2, …, vn} и конечное множество линий Х, соединяющих некоторые пары из точек множества V. Полученная совокупность точек и линий называется графом и обозначается G = {V, X}.
Элементы множества V называются вершинами графа, а элементы множества Х – ребрами.
Граф можно изобразить при помощи геометрической конфигурации. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины (рис. 4). При этом несущественным является расположение вершин, форма и длина ребер графа, важно лишь, соединены две данные точки ребром, или нет.
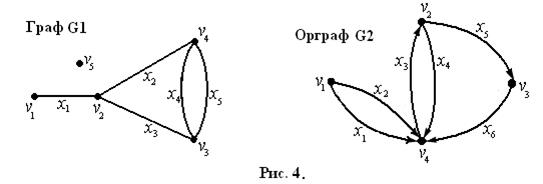Ребра, соединяющие одну и ту же пару вершин, называются кратными (или параллельными) ребрами (ребра х4, х5 графа G1 на рис. 4).
Если х – ребро графа, соединяющее вершины vi, vj, то вершины vi и vj называются концами ребра х.
Множество ребер графа Х можно задать, как множество пар вершин из множества V. Если пары в этом множестве Х являются упорядоченными, то граф называется ориентированным или орграфом. Ребра орграфа называют дугами и на рисунках помечают стрелками (рис. 4).
Если х = (vi, vj) – дуга орграфа, то вершина vi называется началом дуги х, а вершина vj – концом дуги х.
При помощи графов удобно изображать связь атомов в молекуле, кристаллические решетки, схемы дорог, маршруты движения, электрические цепи, экономические связи объектов, графики работ и др.
|
|
|
