 |
Решение примерного варианта контрольной работы
|
|
|
|
Задача 1. Дана формула алгебры логики: 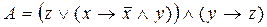 .
.
Требуется:
1) при помощи равносильных преобразований упростить формулу;
2) построить релейно-контактные схемы для исходной и упрощенной формул.
Решение.
1). Упростим заданную формулу, используя принятый порядок выполнения операций  . Сначала выразим импликации через дизъюнкции согласно формуле 12 основных равносильностей:
. Сначала выразим импликации через дизъюнкции согласно формуле 12 основных равносильностей:
x ® y º  Ú y
Ú y 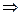 x ®
x ®  Ù y º
Ù y º  Ú (
Ú (  Ù y), y ® z º
Ù y), y ® z º  Ú z,
Ú z,
затем используем формулы 16, 11 и 21:
x Ù y º y Ù x 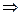
 Ù y º y Ù
Ù y º y Ù  ,
,  Ú z º z Ú
Ú z º z Ú  ,
,
x Ú (y Ù x) º x 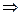
 Ú (y Ù
Ú (y Ù  ) º
) º  ,
,
x Ú (y Ù z) º (x Ú y) Ù (x Ú z) 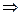 (z Ú
(z Ú  ) Ù (z Ú
) Ù (z Ú  ) º z Ú (
) º z Ú (  Ù
Ù  ),
),
откуда получаем: 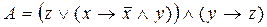 º
º
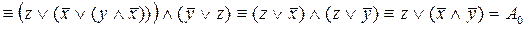 .
.
2). Построим РКС для исходной формулы А, используя таблицу простейших РКС и соответствующих им формул логики:
– конъюнкции  Ù y соответствует последовательное соединение элементов
Ù y соответствует последовательное соединение элементов  и y;
и y;
– импликации x ®  Ù y соответствует параллельное соединение элементов
Ù y соответствует параллельное соединение элементов  и (
и (  Ù y);
Ù y);
дизъюнкции z Ú (x ®  Ù y) соответствует параллельное соединение элементов z и (x ®
Ù y) соответствует параллельное соединение элементов z и (x ®  Ù y);
Ù y);
– импликации y ® z соответствует параллельное соединение элементов  и z;
и z;
– конъюнкции  соответствует последовательное соединение элементов (z Ú (x ®
соответствует последовательное соединение элементов (z Ú (x ®  Ù y)) и (y ® z).
Ù y)) и (y ® z).
Построим РКС для упрощенной формулы  : конъюнкции
: конъюнкции  Ù
Ù  соответствует последовательное соединение элементов
соответствует последовательное соединение элементов  и
и  , а дизъюнкции z Ú (
, а дизъюнкции z Ú (  Ù
Ù  ) соответствует параллельное соединение элементов z и (
) соответствует параллельное соединение элементов z и (  Ù
Ù  ).
).
Полученные в результате РКС изобразим на рис. 5.
Ответы:
1) результат упрощения формулы A:  ;
;
2) РКС, соответствующие исходной формуле А и упрощенной формуле А0 приведены на рис. 5.

Задача 2. Дана булева функция f (x, y) = (x Ú y) ® (x Ù 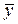 Ú
Ú  ®
® 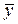 ). Составить таблицу значений функции и указать значение f (0, 1).
). Составить таблицу значений функции и указать значение f (0, 1).
|
|
|
Решение. Известно, что порядок выполнения операций определен следующим образом:  . Используя таблицы истинности для отрицания, конъюнкции, дизъюнкции, импликации составим вспомогательную таблицу значений каждой из операций функции f (x, y).
. Используя таблицы истинности для отрицания, конъюнкции, дизъюнкции, импликации составим вспомогательную таблицу значений каждой из операций функции f (x, y).
| x | y | x Ú y | 
| 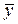
| x Ù 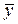
| x Ù 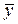 Ú Ú 
| x Ù 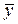 Ú Ú  ® ® 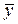
| (x Ú y)®
(x Ù 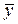 Ú Ú  ® ® 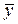 ) )
|
Составим таблицу значений функции f (x, y):
| x | y | f (x, y) = (x Ú y)®(x Ù  Ú Ú  ® ®  ) )
|
По таблице значений функции найдем значение f (0, 1), соответствующее значениям аргументов x = 0, y = 1 (третья строка): f (0, 1) = 0.
Ответы: таблица значений функции приведена выше; f (0, 1) = 0.
Задача 3. Составить список дуг ориентированного графа, изображенного на рисунке 6. Сформировать матрицу инцидентности и матрицу смежности этого орграфа.
 Решение.
Решение.
1. Для составления списка дуг орграфа G составим вспомогательную таблицу, каждая строка которой соответствует одной дуге. В строке записываем обозначение дуги и номера вершин, инцидентных этой дуге, причем сначала указываем начальную вершину, затем – конечную, т. к. граф ориентированный.
| Дуга | Вершины |
| x1 | v2, v1 |
| x2 | v2, v3 |
| x3 | v1, v4 |
| x4 | v4, v1 |
| x5 | v2, v4 |
Получаем список дуг орграфа:
X = {(v2, v1), (v2, v3), (v1, v4), (v4, v1), (v2, v4)}.
2. Для построения матрицы инцидентности орграфа G составим таблицу, используя формулы (1). Заполняем таблицу по столбцам, соответствующим дугам орграфа: в j-м столбце ставим i-й строке «–1», если вершина vi является началом дуги хj, ставим «1», если вершина vi является концом дуги хj и ставим «0», если вершина vi и дуга хj неинцидентны.
При заполнении таблицы можно использовать список дуг орграфа.
|
|
|
| x1 | x2 | x3 | x4 | x5 | Получили матрицу инцидентности: В(G2) = | |
| v1 | –1 | |||||
| v2 | –1 | –1 | –1 | |||
| v3 | ||||||
| v4 | –1 |
3. Для построения матрицы смежности орграфа G составим таблицу, используя формулы (2). Так как граф G ориентированный, то элемент матрицы aij равен количеству ребер с началом в i-й вершине, а концом в j-й вершине.
| v1 | v2 | v3 | v4 | Получили матрицу смежности A(G) = | |
| v1 | |||||
| v2 | |||||
| v3 | |||||
| v4 |
Ответы: список дуг орграфа X = {(v2, v1), (v2, v3), (v1, v4), (v4, v1), (v2, v4)};
матрица инцидентности и матрица смежности:
В(G) = 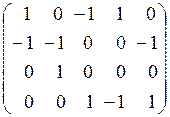 ; A(G) =
; A(G) = 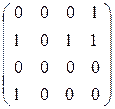 .
.
Задача 4. Дан функционал  . Найти экстремали функционала, удовлетворяющие граничным условиям y(0) = –1, y(π ) = 0.
. Найти экстремали функционала, удовлетворяющие граничным условиям y(0) = –1, y(π ) = 0.
Решение. Запишем уравнение Эйлера  = 0 для данного функционала.
= 0 для данного функционала.
Для подынтегральной функции 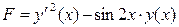 получаем частные производные:
получаем частные производные:

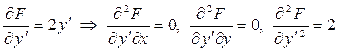 .
.
Тогда уравнение Эйлера имеет вид: 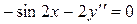 или
или  – простейшее дифференциальное уравнение второго порядка. Его общее решение получаем двукратным интегрированием:
– простейшее дифференциальное уравнение второго порядка. Его общее решение получаем двукратным интегрированием:
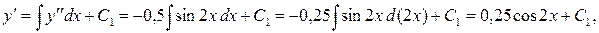

 .
.
Определим произвольные постоянные С1, С2 из граничных условий

Отсюда получаем С1 = 1/π , С2 = –1, следовательно, экстремалью функционала является функция  .
.
Ответ.  .
.
Задача 5. Дана модель объекта управления, описываемая системой дифференциальных уравнений  и граничными условиями x1(0) = 0, x2(0) = 3, x1(3) = 2, x2(3) = –1, где t – время (t
и граничными условиями x1(0) = 0, x2(0) = 3, x1(3) = 2, x2(3) = –1, где t – время (t 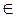 [0; 3]),
[0; 3]),  – фазовый вектор (траектория объекта), u(t) – функцияуправления объектом.
– фазовый вектор (траектория объекта), u(t) – функцияуправления объектом.
Требуется найти оптимальное управление объектом u*(t) и соответствующую ему оптимальную траекторию 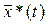 , если задан критерий качества управления:
, если задан критерий качества управления: 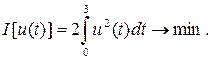
Решение.
1. Введем вспомогательный вектор 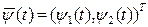 , где
, где  – неизвестные функции, и построим гамильтониан данной задачи:
– неизвестные функции, и построим гамильтониан данной задачи:

 =
=
 ,
,
где функции  – это правые части дифференциальных уравнений
– это правые части дифференциальных уравнений  а
а 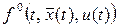 – подынтегральная функция критерия качества управления
– подынтегральная функция критерия качества управления  .
.
По условию задачи 

Отсюда получаем  =
=  .
.
2. Находим максимум гамильнониана по управлению:  ,
,  – критическая точка. Вторая производная
– критическая точка. Вторая производная  , следовательно, при
, следовательно, при  достигается максимум гамильнониана по управлению.
достигается максимум гамильнониана по управлению.
3. Составим каноническую систему дифференциальных уравнений, подставив в формулу (8)  и частные производные гамильнониана
и частные производные гамильнониана  , и решим эту систему. Каноническая система имеет вид:
, и решим эту систему. Каноническая система имеет вид:
|
|
|

Общее решение системы находим последовательным интегрированием:
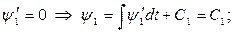
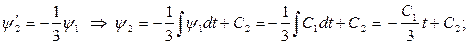


 .
.
Найдем частное решение системы, удовлетворяющее граничным условиям x1(0) = 0, x2(0) = 3, x1(3) = 2, x2(3) = –1.
Из первых двух условий получаем: 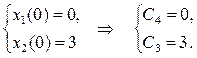
Подставив эти значения в другие два условия  получаем:
получаем:

Вычитая из 1-го уравнения 2-е, получаем  , затем
, затем 
Подставив найденные значения констант, получим оптимальную траекторию и оптимальное управление:
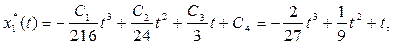


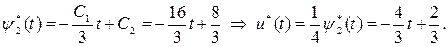
Ответы: оптимальная траектория 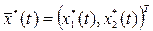 , где
, где 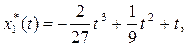
 ; оптимальное управление
; оптимальное управление 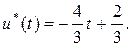
|
|
|


