 |
3.2. Матрицы графов. 4. Элементы вариационного исчисления. 4.1. Функционалы в линейном нормированном пространстве
|
|
|
|
3. 2. Матрицы графов
Для того, чтобы задать граф, необходимо задать множества его вершин и ребер(V и X). Иногда граф задают списком ребер (дуг), например, орграф G2, изображенный на рис. 4, можно задать следующим списком дуг:
X = {х1, х2, х3, х4, х5, х6} = {(v1, v4), (v1, v4), (v4, v2), (v2, v4), (v2, v3), (v3, v4)}.
В этом списке каждой из 6-ти дуг орграфа соответствует упорядоченная пара вершин (если граф неориентированный, то порядок записи вершин в каждой паре – произвольный).
Если граф содержит изолированные вершины, т. е. не связанные ни с одной другой вершиной ребрами (дугами) графа (см. вершину v5 в графе G1 на рис. 4), то список ребер не даст полного представления о графе. Кроме того, использовать список ребер (дуг) можно только при относительно небольшом количестве вершин графа. Для практического использования более удобен матричный способ задания графов.
Пусть G = {V, X} – граф, где V = {v1, v2, …, vn}, X = {x1, …, xm}.
Если вершины графа vi, vj являются концами ребра х, то говорят, что вершины vi, vj и ребро х инцидентны.
Матрицей инцидентности графа G называется матрица размерности n´ m B(G), элементы которой
bij =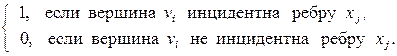 
Строки матрицы инцидентности графа соответствуют его вершинам, а столбцы – ребрам.
Для орграфа вершина vi идуга хj инцидентны, если vi является началом или концом дуги хj. Элементы матрицы инцидентности орграфа определяются по формулам:
bij =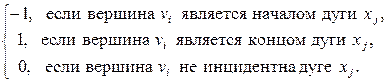 
(1)
Вершины vi, vj графа G называются смежными, если существует ребро х = (vi, vj)Î X, инцидентное этим вершинам (соединяющее эти вершины).
Матрицей смежности графа G называется квадратная матрица A(G) порядка п, каждый элемент которой aij равен количеству ребер, инцидентных вершинам vi и vj.
Для орграфа G = {V, X} элементы матрицы смежности определяются по формулам:
|
|
|
aij = 
(2)
Пример. Записать матрицу инцидентности и матрицу смежности для орграфа G2, изображенного на рис. 4.
Решение. Данный граф является ориентированным. Для построения матрицы инцидентности составим таблицу, используя формулы (1). Заполняем таблицу по столбцам, соответствующим дугам орграфа: в j-м столбце ставим в i-й строке
«–1», если вершина vi является началом дуги хj,
«1», если вершина vi является концом дуги хj,
«0» в остальных случаях (вершина vi и дуга хj неинцидентны).
| x1 | x2 | x3 | x4 | x5 | x6 | Получили матрицу инцидентности: В(G2) = | |
| v1 | –1 | –1 | |||||
| v2 | –1 | –1 | |||||
| v3 | –1 | ||||||
| v4 | –1 |
.
Для построения матрицы смежности составим таблицу, используя формулы (2). Так как граф G2 ориентированный, то элемент матрицы aij равен количеству ребер с началом в i-й вершине, а концом в j-й вершине.
| v1 | v2 | v3 | v4 | Получили матрицу смежности A(G2) = | |
| v1 | |||||
| v2 | |||||
| v3 | |||||
| v4 |
Матрица инцидентности более информативна, чем матрица смежности, т. к. по ней можно восстановить не только нумерацию вершин и связи между ними, но и нумерацию ребер. Однако, при помощи матрицы инцидентности задают только графы, не имеющие изолированных вершин (в матрице смежности изолированной вершине соответствуют нулевая строка и нулевой столбец).
Кроме матриц инцидентности и смежности существуют и другие формы матричного задания графов. Матричный метод задания графов удобен для обработки данных на ЭВМ.
4. Элементы вариационного исчисления
4. 1. Функционалы в линейном нормированном пространстве
Линейным пространством Е называется множество элементов
{x, y, z, …. }, в котором определены операции сложения элементов и умножения элемента на число, удовлетворяющие 8 свойствам:
|
|
|
1. x + y = y + x 
;
2. (x + y) + z = x + (y + z) 
;
3. λ (mx) = (λ m) x 
, где λ , m – числа;
4. (λ + m) x = λ x + mx , где λ , m – числа;
5. λ (x + y) = λ x + λ у , где λ – число;
6. 1·x = x ;
7. существует нулевой элемент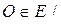 
O + x = x ;
8. для существует противоположный элемент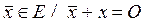 
.
Примеры линейных пространств:
• координатное пространство Rn с элементами – n-мерными векторами либо точками;
• пространство матриц размерности 
;
• Cn[a; b] – пространство функций, непрерывных на промежутке [a; b] вместе со своими производными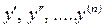 
.
В линейном пространстве вводится понятие нормы элемента.
Нормой элемента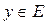 
называется число, обозначаемое 
и удовлетворяющее трем условиям:
1. 
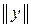³ 0 и 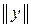= 0 тогда и только тогда, когда у = О;
2. 
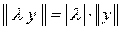
, где λ – число;
3. 
, где λ – число.
Пример. В пространстве C[a; b] (пространство функций, непрерывных на промежутке [a; b]) норма элемента у может быть введена следующим образом:
.
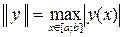Если каждой функции из некоторого линейного нормированного пространства функций У ставится в соответствие число, то говорят, что на множестве У задан функционал I [y (x)].
Примеры функционалов.
• 
– функционал, заданный на пространстве функций, имеющих непрерывные производные на промежутке [a; b], т. е. на C1[a; b];
• 
– функционал, заданный на пространстве функций, интегрируемых на промежутке [0; 1].
Рассмотрим пространство C[a; b] – множество функций (кривых), непрерывных на промежутке [a; b], и функционал I [y (x)], определенный на этом пространстве.
ε -окрестностью кривой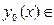 
C[a; b] называется совокупность кривых 
C[a; b], таких что
.
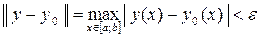Разность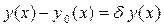 
называется вариацией аргумента функционала. Вариация d y (x) есть функция от x и тоже принадлежит функциональному пространству C[a; b].
Приращением функционала называется разность DI = I [y(x)] – I [y0(x)], где y0(x) – фиксированная функция, а y (x) – произвольная функция из пространства C[a; b].
Используя вариацию d y (x), можно представить приращение функционала в виде 
.
Линейным функционалом называется функционал I [y (x)], удовлетворяющий следующим условиям:
1) I [λ y (x)] = λ I [y (x)], где λ – число;
2) I [y1(x) + y2(x)] = I [y1(x)] + I [y2(x)].
Вариацией функционала называется главная часть его приращения, линейная относительно d y (x).
Если приращение функционала можно представить в виде
|
|
|
,
где 
– линейный функционалотносительно d y (x), и функционал 
при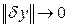 
, то d I [y] = 
– вариация функционала I [y (x)].
|
|
|
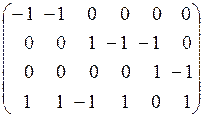