 |
Математические модели основных термодеформационных процессов, протекающих в зоне точечной сварки
|
|
|
|
Нагрев и пластическая деформация металла в зоне сварки относятся к термодеформационным процессам, наиболее значимо влияющим на устойчивость процесса формирования соединения и во многом предопределяющим его конечные результаты. Это можно считать признанным всеми специалистами. Если нагреву посвящено много экспериментальных и теоретических исследований, предложено большое количество расчетных методик определения его параметров, как аналитических, так и численных, то сведения о процессах пластических деформаций носят в основном самый общий характер. Практически отсутствует их математическое описание (см. раздел 2.5). Вместе с тем, очевидно, что при отсутствии математических моделей этих процессов, методик расчетов количественных значений их параметров, ни о каком научно обоснованном программировании параметров режима точечной сварки не может быть и речи, не говоря уже о создании систем автоматического проектирования технологических процессов (САПР ТП).
Оптимизация параметров силового и энергетического воздействия на детали в современных способах КТС, в том числе и с программированием их параметров режима, затруднительна без определения количественного соотношения между параметрами основных термодеформационных процессов, протекающих в зоне формирования сварного соединения. Определение же количественного соотношения между параметрами основных термодеформационных процессов, протекающих в зоне сварки, невозможно без формального математического их описания, то есть без разработки их математических моделей.
Точное описание формальным языком изменения параметров термодеформационных процессов, протекающих в зоне формирования соединения, а также их взаимозависимости и взаимовлияния, затрудняются их сложностью и динамичностью. Поэтому наиболее рациональным методом решения поставленной задачи является метод идентификации реальных процессов с идеализированными моделями, которые представляется возможным описать математическим языком.
|
|
|
Разработка математической модели термодеформационного равновесия процесса точечной сварки по существу представляет собой математическое описание физической модели процесса формирования соединения, описанной выше в п. 2.5.2. Иными словами, математическая модель термодеформационного равновесия процесса КТС — это математическое описание напряженно-деформированного состояния металла в зоне сварки при формировании точечного сварного соединения. Она основана на результатах экспериментальных исследований процесса сварки, в частности, на вышеуказанном выводе о том, что между тепловыми и деформационными процессами в зоне формирования соединения должно существовать определенное равновесное соотношение, которое зависит от режима сварки, теплофизических свойств металла и геометрических параметров деталей и электродов. При этом подразумевается, что при условиях формирования точечного сварного соединения, близких к условиям оптимальным, система электрод–детали–электрод в силовом отношении замкнута, и силы, действующие на каждый ее элемент, уравновешены в любой момент процесса сварки. Нагрев, разупрочнение, плавление, дилатация и пластическая деформация металла в зоне сварки не нарушают этого равновесия. Выплески же или непровары являются следствием нарушения этого равновесного состояния, вызванного воздействием каких-либо возмущающих факторов. Экспериментальным подтверждением сказанного выше являются как пространственная неподвижность зоны сварки, так и изменение площадей контактов деталь–деталь и электрод–деталь в процессе формирования соединения.
|
|
|
3.1 Термодеформационное равновесие силовой системы
электрод - детали – электрод при традиционных способах сварки
Математическая модель [205, 206], описывающая силовое взаимодействие свариваемых деталей и электродов в контактах деталь–деталь и электрод–деталь, по существу представляет собой математическое описание силового равновесия деталей в процессе формирования соединения при контактной точечной сварке.
Рассмотрим элемент системы электрод–детали–электрод — одну свариваемую деталь, в равновесии в какой-либо фиксированный момент времени t после момента t НП начала плавления металла в контакте деталь–деталь до момента t СВ окончания его нагрева, т. е. при 
(рис 3.1). Равновесие свариваемой детали в дискретный момент t будем рассматривать в цилиндрической системе координат.
Пусть в какой-либо дискретный момент времени t распределение нормальных, относительно плоскости свариваемого контакта, напряжений по площади S Э t контакта электрод–деталь описывается функцией:
[1], (3.1)
а по площади S П t свариваемого контакта, внутри контура уплотняющего пояска, функцией:
. (3.2)
В свариваемых деталях наблюдается растекание сварочного тока и угол α между линиями тока j в приконтактных областях деталей меньше 180°. А поскольку ток в них протекает в противоположных направлениях, то между этими линиями тока действуют элементарные электродинамические силы отталкивания Fj, которые стремятся раздвинуть и свариваемые детали. Пусть их распределение по площади Sjt растекания тока, приведенное к плоскости свариваемого контакта и направленных нормально к ней, описывается функцией:
. (3.3)
В работах [3, 16, 207] показано, что давление расплавленного металла в ядре имеет градиент по координате r, который обусловлен воздействием магнитного поля на жидкий металл. Поэтому распределение давления по площади S Я t ядра в плоскости свариваемого контакта в общем случае следует описывать функцией координат r и φ:
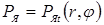. (3.4)
|
|
|
При сближении свариваемых деталей из-за упругой их деформации в них возникают напряжения. Составляющие этих напряжений, нормальные к плоскости свариваемого контакта, препятствуют сближению свариваемых деталей, т. е., как показано в п. 2.1.2, они уравновешивают часть усилия сжатия электродов. Пусть распределение этих напряжений по цилиндрической поверхности, образующая которой параллельна оси электродов, а направляющей является граница контакта деталь–деталь, и ограниченной плоскостями поверхностей свариваемых деталей, описывается функцией:
. (3.5)
Для того, чтобы эта система, имеющая одну степень свободы — возможность перемещения в направлении оси электродов, находилась в равновесии, необходимо, чтобы сумма проекций всех сил на координату z равнялась нулю. В данном случае это условие равновесия можно записать следующим образом:
,
где β1, β2, β3, β4, β5 — углы между соответствующими элементарными силами и координатой z, в данном случае равные нулю, потому что по принятым в зависимостях (3.1)…(3.5) условиям элементарные силы нормальны к плоскости свариваемого контакта; dS — площадь действия элементарной силы.
При условии равенства нулю углов β соответствующие значения 
будут равны единице. Тогда написанное выше уравнение равновесия можно преобразовать к следующему виду:
. (3.6)
Условие равновесия (3.6) фактически является интегральным и в цилиндрической системе координат, в интегральной форме может быть записано следующим образом:
, (3.7)
где Lt – контур контакта деталь–деталь.
Данное интегральное условие равновесия включает в себя два важных взаимосвязанных технологических параметра: напряжения в контакте электрод–деталь — 
, и площадь уплотняющего пояска — S П t, т. е. параметры внешнего силового воздействия на зону сварки и деформирования в ней металла. Это дает возможность при известных остальных его составляющих, выражающих параметры внутренних термодеформационных процессов, определять величину одного из них при заданном значении другого. Кроме того, все составляющие условия (3.7) зависят от термодинамического состояния металла в зоне сварки, характеризуемого температурой и фазовым состоянием, а потому описывают изменение и взаимовлияние всех основных термодеформационных процессов, протекающих в зоне сварки. Поэтому его можно назвать «уравнением термодеформационного равновесия процесса контактной точечной сварки».
|
|
|
Точные вычисления непосредственно по уравнению (3.7) весьма затруднительны. Это объясняется отсутствием или сложностью аналитических решений ряда частных задач, входящих в данное уравнение. Например, таких, как распределение напряжений в контактах и их изменение в ходе процесса формирования соединения, определение значений давления в ядре и его градиента в плоскости свариваемого контакта, а также функций, точно описывающих граничные условия и их изменение в процессе сварки. Поэтому для приближенных решений технологических задач уравнение (3.7) целесообразно упростить.
Допущение об осесимметричности зоны формирования соединения при КТС значительно упрощает определение пределов интегрирования. Тогда, для рассматриваемой в равновесии одной детали уравнение (3.7) можно переписать со следующими пределами интегрирования:
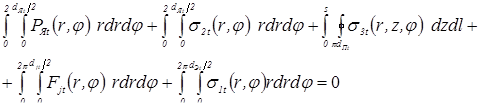, (3.8)
где s – толщина свариваемых деталей, d Я t, d П t, d Э t, djt, – диаметры соответственно ядра, контакта деталь–деталь, контакта электрод–деталь и площади растекания линий сварочного тока в момент времени t.
Приближенные вычисления значений Fjt показали, что при применяемых режимах сварки электродинамические силы, раздвигающие свариваемые детали из-за растекания в них сварочного тока, очень малы и составляют незначительную часть от сварочного усилия (меньше 0,5 %). Поэтому, при приближенных технологических расчетах этими силами можно пренебречь и 4-й интеграл в (3.8) можно принять равным нулю:
.
Очевидно, что интегрирование напряжений в контакте электрод-деталь по площади этого контакта, при любом их распределении, даст величину, равную усилию сжатия деталей электродами. Поэтому 5-й интеграл в (3.8), выражающий сумму напряжений в площади контакта электрод–деталь, можно принять равным усилию сжатия электродов F Э t в момент времени t:
.
Третий интеграл в (3.8), описывающий сумму напряжений от упругой деформации деталей при их прогибе, после вычислений по цилиндрической поверхности равен усилию F Д t, которое необходимо для сближения свариваемых деталей до их соприкосновения:
.
Усилие F Д t в условиях сварки может достигать 10 % [100]. Оно практически не изменяется в процессе формирования соединения [81] и при выборе режимов сварки может учитываться как постоянная составляющая. При приближенных технологических расчетах величину F Д t можно вычислять по зависимости (2.5).
|
|
|
Приближенные расчеты по зависимостям, приведенным в работах [3, 16, 207] показали, что градиент давления в ядре, обусловленный электродинамическим действием сварочного тока, не превышает 5 % от средней его величины, которая определяется термодеформационными процессами в зоне сварки. Поэтому, с целью упрощения расчетов, можно считать, что градиент давления в ядре отсутствует, т. е. допустить, что давление в ядре постоянно по всему объему и не зависит от координат r и φ. Тогда после вычисления 1-го интеграла в (3.8), который выражает величину усилия F Я t,развиваемого давлением жидкого металла в площади ядра, получаем:
, (3.9)
где РЯ t – среднее значение давления расплавленного металла в ядре;
Напряжения во 2-м интеграле уравнения (3.8), который выражает сумму нормальных напряжений в площади уплотняющего пояска, рационально учитывать через их среднее значение, не зависящее от координат r и φ. По теореме о среднем [208] — среднее значение напряжений в площади уплотняющего пояска σСР t можно выразить следующим образом:
.
Отсюда интеграл, который выражает сумму нормальных напряжений в площади уплотняющего пояска, можно определить следующим образом:
, (3.10)
где F П t – усилие в площади уплотняющего пояска.
Тогда интегральное уравнение (3.8) термодеформационного равновесия процесса формирования соединений при традиционных способах КТС можно, с учетом сказанного выше, преобразовать к окончательному виду, удобному для практических расчетов:
, (3.11)
где, для момента времени t, d Я t и d П t – диаметры, соответственно, ядра расплавленного металла и уплотняющего пояска; P Я t – давление расплавленного металла в ядре; σ СР t – среднее значение нормальных напряжении в площади уплотняющего пояска; F Д t – усилие, необходимое для сближения свариваемых деталей до соприкосновения их поверхностей; F Э t – усилие сжатия деталей электродами.
Уравнение термодеформационного равновесия процесса контактной точечной сварки (3.11) позволяет для любого момента процесса формирования соединения решать две задачи.
Первая из этих задач — технологическая. Решение данной задачи позволяет рассчитывать усилие сжатия электродов F Э t, как параметр режима сварки, которое необходимо для формирования уплотняющего пояска заданного диаметра d П t, величину которого можно задавать из условия устойчивого формирования соединения при КТС.
Вторая задача — исследовательская. Ее решение может быть использовано при отработках новых технологий КТС. При решении этой задачи, наоборот, для любого момента процесса формирования соединения, по уравнению (3.11) можно рассчитывать диаметр уплотняющего пояска d П t при заданном значении усилия сжатия электродов F Э t.
Очевидно, что оба этих решения имеют большое практическое значение. Первое решение позволяет определить требуемое усилие сжатия электродов при выборе режимов сварки, а второе — моделировать термодеформационные процессы, протекающие в зоне сварки. При этом, для решении любой из этих задач необходимо для любого момента процесса сварки определять все составляющие уравнения (3.11), т. е. количественно определять параметры основных термодеформационных процессов, которые протекают в зоне формирования соединения.
3.2. Термодеформационное равновесие силовой системы
электрод-детали-электрод при контактной точечной сварке
с обжатием периферийной зоны соединения
Способы КТС с обжатием периферийной зоны соединений, описанные в п. 1.2.3, в которых обжатие осуществляют в области уплотняющего пояска (см. рис. 1.7), не нашли широкого практического применения в основном из-заотносительно низкой стойкости токопроводящего электрода. Причиной этого является то, что обжатие деталей в области уплотняющего пояска вызывает необходимость уменьшения внутреннего диаметра обжимной втулки и, следовательно, наружного диаметра рабочей части токопроводящего электрода до значений, близких к диаметру ядра, которые значительно меньше стандартных. В результате токопроводящий электрод перегревается из-за высокой плотности тока и ухудшения условий его охлаждения вследствие уменьшения площади сечения его токопроводящей части. В связи с этим был разработан способ КТС с обжатием периферийной зоны соединений вне контура уплотняющего пояска, в котором силовое взаимодействие деталей значительно сложнее, чем при традиционных способах КТС, и уже не описывается уравнением (3.11).
|
|
|
