Методика расчета среднего значения нормальных напряжении в контакте деталь - деталь

Точно рассчитать распределение напряжений в контактах при КТС по-видимому не представляется возможным из-за сложности и динамичности, протекающих в них термодеформационных процессов. Приближённое решение данной задачи [206, 217, 218] основано на допущении, что характер распределения напряжений в контакте деталь–деталь при точечной сварке подобен характеру распределения напряжений в контакте пуансон–деталь при осадке полосы. Это предположение сделано на основании анализа опубликованных работ С. И. Губкина, Е. П. Унксова, В. В. Соколовского и других исследователей, посвященных определению напряжений в контактах. Ими установлено, что в общем случае в площади контакта имеется три участка, которые отличаются распределением касательных напряжений (рис. 3.19). Качественно такой характер распределения нормальных напряжений в контактах электрод–деталь и деталь–деталь при точечной сварке подтверждается экспериментами по затеканию (пластической деформации) металла в узкую щель в электроде (рис. 3.20) и характером деформации периодического рельефа на поверхности детали (рис. 3.21).

Можно предположить, что и при сварке в площади контакта в момент времени t имеется три участка (рис 3.19 и 3.22), отличающихся распределением касательных напряжений τ,подобно осадке полосы [219]:

1) зона скольжения (участки a ₁ b ₁ и b ₂ a ₂) ;

2) зона торможения (участки b ₁ c ₁ и c ₂ b ₂) ;

3) зона застоя (участки c ₁ о и о c ₂) ;

где σ _Z — напряжения, нормальные к плоскости свариваемого контакта;
μ — коэффициент трения; r — радиальные координаты точек в плоскости поверхности деталей.

Наличие таких участков в контактах при КТС экспериментально подтверждается, например, в работе [129].

Решением приближенного уравнения равновесия, предложенного
Е. П. Унксовым [219, 220],

,

где s — толщина детали; σ _z, σ _r, и σ_θ — соответственно, нормальные относительно плоскости свариваемого контакта, радиальные и окружные напряжения; совместно с условием пластичности Губера – Мизеса

,                                  (3.45)

где σ_Д — это сопротивление пластической деформации металла в области уплотняющего пояска; получены функции, описывающие изменение нормальных напряжений σ_{1 Z}, σ_{2 Z}, σ_{3 Z} на различных участках контакта, которые, применительно к условиям точечной сварки, имеют следующий вид:

- первый участок при r_b ≤ r ≤ r_a

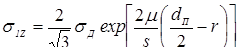;                            (3.46)

- второй участок при r_c ≤ r ≤ r_b

;                        (3.47)

- третий участок при 0 ≤ r ≤ r_c

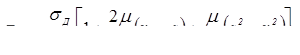.                (3.48)

Здесь μ – коэффициент трения; d _П – диаметр контурной площади контакта (уплотняющего пояска).

Координату границы зоны торможения r_b можно определить по зависимости, приведенной в работе [221], которая, применительно к условиям точечной сварки имеет вид

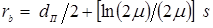.                           (3.49)

Поскольку при КТС в контакте электрод–деталь и, в особенности, деталь–деталь наблюдается схватывание металла [128, 129], то коэффициент трения μ можно принять равным 0,5. Тогда, согласно (3.49) при μ = 0,5 — координата , т. е. зона скольжения (участки a ₁ b ₁ и a ₂ b ₂) отсутствуют, а зона торможения (участки b ₁ c ₁ и b ₂ c ₂) доходит до границы контакта.

Расчеты показали, что, пренебрегая уменьшением касательных напряжений в зоне застоя (с₁о и ос₂ (см. рис. 3.19)), получаем абсолютную ошибку при определении средней величины нормальных напряжений σ_СР, не превышающую 5...10 %, причем в свариваемом контакте только до начала плавления металла. Поэтому, чтобы упростить расчеты, можно допустить, что распределение касательных напряжений τ в области 0 ≤ r ≤ d _П / 2 равномерно и зона торможения распространяется до центра контакта, т. е. r _С = 0.

Тогда по известной теореме о среднем, после подстановки в нее зависимости (3.47), среднее значение сжимающих нормальных напряжений в свариваемом контакте σ_{СР t} в любой момент процесса формирования соединения t можно определить следующим образом

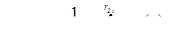,                                 (3.50)

где r _{1 t} и r _{2 t} – соответственно нижний и верхний пределы интегрирования.

При КТС нижний r _{1 t} и верхний r _{2 t} пределы интегрирования изменяются в течение процесса формирования соединения. До момента начала образования ядра контакт твердого металла осуществляется по всей площади уплотняющего пояска. Поэтому в этот период пределы интегрирования r _{1 t} = 0 и r _{2 t} = d _{П t} / 2 и интегрирование зависимости (3.47) следует проводить в интервале 0… d _{П t} / 2. При появлении ядра контакт твердого металла осуществляется по уплотняющему пояску шириной b _{П t} = d _{П t} / 2 – d _{Я t} / 2. Следовательно, интегрирование зависимости (3.47) в этот период следует проводить в интервале d _{Я t} / 2… d _{П t} / 2. Поскольку до начала плавления металла d _{Я t} = 0, то интервал интегрирования d _{Я t} / 2… d _{П t} / 2 может быть принят для любого момента КТС при 0 ≤ t ≤ t _СВ. Тогда, после подстановки в (3.50) зависимостей (3.47) и (3.49) количественное значение σ_{СР t} можно определить следующим интегральным выражением

,

из которого после вычисления интеграла с вышеуказанными переменными пределами интегрирования получаем формулу для приближенных количественных расчетов среднего значения нормальных напряжений σ_{СР t} в контакте деталь–деталь в любой момент t процесса формирования соединения

.                        (3.51)

Здесь, для момента t процесса формирования соединения, σ_{Д t} — сопротивление деформации металла; d _{Я t} и d _{П t} — текущие значения диаметров, соответственно, ядра и уплотняющего пояска; К_σ – коэффициент, характеризующий неравномерность распределения в площади контакта нормальных напряжений по координате r, который для условий КТС следует принимать в пределах 0,25...0,5.

Согласно выражению (3.47) напряжения σ_{2 Z} на краю контакта при 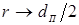 во всех случаях стремятся к значениям сопротивления деформации металла 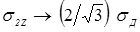, а в центре контакта при  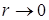они растут с увеличением отношения диаметра контакта к толщине детали : . Это изменение неравномерности распределения напряжений по координате r, как следует из формулы (3.51), существенно влияет и на средние их значения σ_{СР t} в площади контакта. Так, минимальные значения  получаются при , в случае отсутствия ядра расплавленного металла, или же при уменьшении ширины уплотняющего пояска, т. е. разности  после начала расплавления металла. Причем, это влияние увеличивается с уменьшением толщины свариваемых деталей вследствие увеличения отношения d _{П t} / s.

Точность методики расчета σ_{СР t} до начала плавления металла представляется возможным оценить прямыми измерениями, поскольку при этом условии σ_{СР t} равно среднему давлению в контакте, которое можно определить делением усилия сжатия электродов F _Э на его площадь S _К: . Например, свариваемые детали сжимали между электродами на экспериментальной установке, описанной в п. 2.1.2 (рис. 2.7), и измеряли при этом контурную площадь контакта по методике угольных пленок (рис. 2.3). Затем определяли экспериментальные значения σ_СР и сравнивали их со значениями, рассчитанными по формуле (3.51). Пример такого сравнения для холодных контактов показан на рис. 3.23. Проведенные исследования показали удовлетворительную сходимость экспериментальных (показаны точками) и расчетных (кривая 1) значений напряжений в контактах.

Все, сказанное выше, не противоречит существующим представлениям о распределении нормальных напряжений в контактах.

 

3.4.2. Методика расчета давления расплавленного металла в ядре

Сведения о давлении расплавленного металла в ядре в литературе по сварке носят в основном предположительно-описательный характер. Это объясняется особенностями точечной сварки, не позволяющими измерить его экспериментально, и сложностью термодеформационных процессов в зоне сварки на стадии нагрева, которая затрудняет расчетное определение его величины.

Ниже изложена методика, разработанная [206, 218, 222] на основании приведенных исследований термодеформационных процессов, протекающих в зоне сварки на стадии нагрева, которая позволяет приближенно рассчитать давление расплавленного металла в ядре в любой момент процесса его формирования. Поставленная цель достигается тем, что реальный процесс пластической деформации металла, окружающего ядро, с определенными допущениями, в частности, об осесимметричности зоны сварки, сводится к решению задачи о деформировании сферической оболочки внутренним давлением Р (рис. 3.24).

Согласно решению данной задачи Ляме [223] компоненты напряжений в сферических полярных координатах определяются зависимостями:

,

,

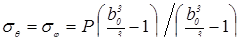где σ _r, и σ_θ, σ_φ — радиальное и окружные напряжения; Р — давление в полости, b ₀ — наружный радиус сферы; а — радиус полости.

Р. Хилл [224], применив условие пластичности Треска – Сен-Венана

,                                      (3.52)

где σ_Т — предел текучести, распространил это решение на случай упругопластического деформирования внутренним давлением толстостенной сферической оболочки. Согласно этому решению распределение напряжений в толстостенной сферической оболочке при упругопластическом ее деформировании внутренним давлением Р (слева на рис. 3.24) описывается следующими зависимостями: в упругой области, при c ≤ r ≤ b ₀

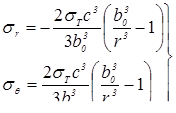,                              (3.53)

в пластической области, при а ≤ r < с

,                 (3.54)

где a — радиус полости; b ₀ — наружный радиус сферы; с — радиус границы пластической области.

В упругой области оба компонента напряжения уменьшаются с увеличением координаты r. В области пластических деформаций с увеличением r радиальное напряжение уменьшается по величине, тогда как, по условию пластичности, окружное напряжение увеличивается. Максимальное значение окружного напряжения достигается на границе пластического и упругого состояний металла (радиус с). Аналогичный характер изменения напряжений по координате r получен при решении подобной задачи и в работе [225].

Экспериментально установлено (см. п. 2.5.2), что на стадии нагрева максимальные относительные пластические деформации свариваемых деталей по координате r, достигающие 15 %, локализованы в области контура сварочного контакта, диаметром d _{П t}, и в узком поясе (шириной
≤ 0,05...0,15 d _{П t}) вокруг него. Упругие же радиальные деформации свариваемых деталей вне этой зоны незначительны, и поэтому ими можно пренебречь. Тогда процесс деформации металла в зоне формирования соединения при контактной точечной сварке можно уподобить процессу деформации металла сферической оболочки с бесконечно толстыми стенками,
т. е. при b ₀ → ∞ (справа на рис 3.24).

Так как металл, выдавливаемый в зазор деталь–деталь, при несвободном расширении в площади уплотняющего пояска, шириной , преодолевает силу реакции противоположной детали, то можно предложить, что он находится в объемно-сжатом напряженном состоянии аналогично металлу зоны а — д при деформации сферической оболочки. При сварке давление в ядре и напряжения в уплотняющем пояске стремятся раздвинуть свариваемые детали аналогично тому, как и давление в полости сферы и напряжения в зоне объемно-сжатого металла
а — д при деформировании сферической оболочки. При деформировании сферической оболочки разъединению полусфер препятствует металл с растягивающими окружными σ_θ напряжениями при r > c, в процессе же сварки разъединению деталей препятствует усилие сжатия электродов F _Э. Поскольку ядро в плоскости свариваемых деталей имеет форму круга, в плоскости оси электродов — эллипса, а пластические деформации металла локализованы в области уплотняющего пояска, то можно допустить, что характер напряженного состояния пластически деформируемого металла в приконтактной области уплотняющего пояска подобен характеру напряженного состояния металла в объемно-сжатой зоне а — д при деформировании сферической оболочки с бесконечно толстой стенкой.

Поэтому процесс деформации металла в зоне сварки на стадии роста ядра можно приближенно уподобить процессу деформации при расширении сферической полости в оболочке с бесконечно толстыми стенками, если оболочку мысленно рассечь по диаметральной плоскости, и сумму растягивающих окружных напряжений σ_θ, при r > д заменить усилием сжатия электродов, т. е. принять, что:

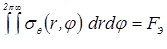.                                (3.55)

Таким образом, определить давление Р в ядре можно, решая задачу только в пластической области, так как упругие деформации влияния на его величину практически не оказывают. При этом контуром уплотняющего пояска можно считать границу металла при деформировании сферической оболочки, находящегося в объемно-сжатом состоянии.

Тогда изменение напряжений по координате r в пластической области (а ≤ r < с) при b ₀ → ∞, согласно зависимостям (3.54) можно описать следующим образом:

.                             (3.56)

Более точные результаты, по мнению ряда исследователей [220, 225], получаются при использовании условия пластичности не Треска – Сен-Венана (3.52), а Губера – Мизеса (3.45).

При высоких скоростях деформации и высокой температуре деформируемого металла, что имеет место при точечной сварке, «деформируемость» металла точнее характеризуется не пределом текучести σ_Т, а сопротивлением пластической деформации σ_Д металла с учетом процессов его упрочнения и разупрочнения [226]. Поэтому для условий пластической деформации металла при точечной сварке предел текучести σ_Т в условии пластичности (3.45) рационально заменить сопротивлением пластической деформации σ_Д. Тогда давление в полости сферической оболочки, которое равно радиальному напряжению металла на поверхности полости, но с обратным знаком, необходимое для осуществления пластического течения металла до радиуса с, по зависимости (3.56) можно рассчитать следующим образом:

.                              (3.57)

Координату пластической области с можно выразить через координату д границы объемно-сжатого металла из зависимостей (3.56), так как при r = д окружные напряжения σ_θ = 0. После преобразований получаем следующее соотношение с и д:

.                              (3.58)

Согласно принятой модели можно записать следующее соотношение координат элементов сферической оболочки и зоны сварки: д = d _{П t} / 2, а
а = d _{Я t} / 2. Причем, значение координаты области пластических деформаций, выраженной зависимостью (3.58), практически совпадает с координатой, полученной при экспериментальных исследованиях пластических деформаций металла в зоне формирования соединения при КТС (см. п. 2.5.2).

С учетом сказанного выше зависимость (3.57) для расчета давления расплавленного металла в ядре Р_{Я t} в любой момент времени t процесса формирования соединений при КТС можно преобразовать к следующему окончательному виду:

,                     (3.59)

где для момента времени t, Р_{Я t} – давление расплавленного металла в ядре; σ_{Д t} –сопротивление пластической деформации металла в области уплотняющего пояска; d _{Я t} и d _{П t} – диаметры, соответственно, ядра и уплотняющего пояска.

Из формулы (3.59) следует, что давление расплавленного металла в ядре прямо пропорционально сопротивлению пластической деформации металла и логарифму отношения диаметра уплотняющего пояска к диаметру ядра. Поэтому давление расплавленного металла в ядре в процессе его формирования может только уменьшаться, поскольку всегда уменьшается как сопротивление деформации металла σ_{Д t}, так и отношение d _{П t} / d _{Я t}. Очевидно, что при при уменьшении ширины уплотняющего пояска, то есть разности , давление в ядре, как средние значения напряжений σ_{СР t}, стремятся к минимальному значению: .

Проверить точность расчетной методики прямым измерением давления расплавленного металла в ядре пока не представляется возможным. Поэтому экспериментальную оценку точности зависимостей для расчета давления в ядре Р_{Я t} (3.59) и средних значений нормальных напряжений σ_{СР t} (3.51) производили косвенно. Такую экспериментальную оценку, пример которой показан на рис. 3.25, осуществляли следующим образом.

Сваривали образцы деталей, последовательно прерывая процесс сварки на различных его стадиях (через 0,02 с). При этом для моментов прерывания измеряли текущие значения (показаны круглыми точками) диаметров уплотняющего пояска (свариваемого контакта) d _П и ядра d _Я (после начала плавления металла). По ним определяли экспериментальные значения среднего давления по площади свариваемого контакта  — (показаны треугольными точками). Кроме того, для этих же моментов процесса сварки, используя измеренные значения d _Я и d _П, рассчитывали Р_Я и σ_СР по зависимостям (3.59) и (3.51), а также значения среднего давления по площади свариваемого контакта 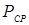 по зависимости:  (значения сопротивления деформации металла σ_{Д t} в зависимостях (3.59) и (3.51) определяли по методике, описанной ниже в разделе 3.5).

Очевидно, что до начала плавления металла (~ 0,375 t _СВ) значения Р_СР и σ_СР совпадают (показаны сплошной линией). После начала плавления металла значения σ_СР меньше, чем значения Р_СР (показаны пунктирной линией), так часть усилия сжатия уравновешивается давлением Р_Я расплавленного металла в ядре.

Об адекватности расчетных значений Р_Я и σ_СР и их значений в реальном процессе КТС судили по расхождению значений  и 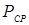 для различных условий сварки (они не превышают 10...20 %). Это, по-видимому, можно считать вполне приемлемым для приближенных методик расчета.

Таким образом, разработанные модели силового взаимодействия деталей в площади свариваемого контакта позволяют в любой момент процесса сварки рассчитать давление расплавленного металла в ядре и величину нормальных напряжений в площади свариваемого контакта. Однако для этого необходимо в любой момент процесса иметь возможность определять сопротивление пластической деформации металла в зоне сварки, величина которого входит в зависимости (3.51) и (3.59).

Предыдущая10111213141516171819202122232425Следующая

Поделиться:

Воспользуйтесь поиском по сайту: