 |
Методики расчета изменения диаметра уплотняющего пояска в процессе контактной точечной сварки
|
|
|
|
Математическое моделированиепроцессов контактной точечной сварки осуществляется решением уравнений термодеформационного равновесия процесса сварки (3.11) или (3.17) относительного диаметра уплотняющего пояска d П t в отдельные дискретные моменты времени t от начала до окончания импульса тока. При этом параметры внешнего силового воздействия на детали (усилия сжатия электродов F Э t) заданы, как параметры режима сварки. В силу использования для оценки теплового состояния зоны сварки расчетно-экспериментального метода, выраженного зависимостью (3.36), подразумевается, что величина сварочного тока заданна такой, чтобы обеспечивала получение заданных геометрических размеров ядра (высоты h Я и диаметра d Я). В процессе решения уравнений (3.11) или (3.17) относительно d П t для каждого момента времени t рассчитывается и все остальные его составляющие, которые отражают изменение термодеформационных процессов, протекающих в зоне сварки на стадии нагрева.
Расчет изменения диаметра уплотняющего пояска в процессе формирования соединения решением уравнений (3.11) или (3.17) относительно d П t осложняется тем, что эти уравнения относительно d П t являются трансцендентными. Поэтому в методиках расчета изменений диаметра уплотняющего пояска в процессе сварки, описанных ниже, решение уравнений (3.11) и (3.17) относительно d П t осуществляется методом итераций.
4.1.1. Методика расчета изменения диаметра уплотняющего пояска
при традиционных способах контактной точечной сварки
Расчет изменения диаметра уплотняющего пояска в процессе формирования соединения при традиционных способах контактной точечной сварки осуществляется  решением уравнения (3.11) относительно d П t для условий сварки деталей одинаковых толщин из одного и того же материала. Алгоритм [206, 210, 253] решения поставленной задачи по моделированию КТС рассчитан на машинный счет и осуществляется следующим образом (рис. 4.1).
решением уравнения (3.11) относительно d П t для условий сварки деталей одинаковых толщин из одного и того же материала. Алгоритм [206, 210, 253] решения поставленной задачи по моделированию КТС рассчитан на машинный счет и осуществляется следующим образом (рис. 4.1).
|
|
|
Блок 2 алгоритма осуществляет ввод исходных данных, которые рационально разбить на три группы. В особенности это целесообразно делать при расчетах нескольких вариантов одного и того же задания.
Первая группа исходных данных предназначена для управления работой программы. В ней задается, например, число шагов расчета по времени, условия вывода результатов расчетов и т. п.
Вторая группа исходных данных содержит параметры теплофизических и прочностных характеристик свариваемого материала (табл. 4.1).
Таблица 4.1
Исходные данные для расчетов по уравнениям термодеформационного
равновесия процесса сварки
| № пп | Параметры | Обозначение | Единицы измерения | ||
| Характеристики свариваемого материала | |||||
| 1 | Температура плавления | ТПЛ | °С | ||
| 2 | Температурный коэффициент линейного расширения | α | 1/оС | ||
| 3 | Коэффициент расширения при плавлении | β* | % | ||
| 4 | Предел текучести | σТ | Па | ||
| 5 | Температура расчёта σТ | Тσ | °С | ||
| 6 | Базисное значение сопротивление деформации | σД0 | Па | ||
| 7 | Данные для аппроксимации изменения термомеханических коэффициентов: кТ, кε и к U и предела текучести σ02 | АТ, ВТ, nT , Аε, Вε, n ε, А u, В u, В σ, nσ | б/р | ||
| 8 | Коэффициент Пуассона | μ | б/р | ||
| 9 | Модуль Юнга | Е | Па | ||
| Данные по технологии и режиму сварки | |||||
| 10 | Толщина свариваемыхдеталей | s | м | ||
| 11 | Конечные диаметр и высота ядра | d Я, h Я | м | ||
| 12 | Шаг между точками * | t | м | ||
| 13 | Ширина нахлёстки * | c | м | ||
| 14 | Величина зазора * | δ | м | ||
| 15 | Радиус или диаметр рабочих поверхностей электродов | R Э, d Э | м | ||
| 16 | Время сварки | t СВ | c | ||
| 17 | Время начала плавления металла** | t НП | c | ||
| 18 | Максимальная температура под электродом ** | ТЭ | °С | ||
| 19 | Коэффициенты для формул (3.36) и (3.51) | m 1, n 1, m 2, n 2, Кσ | б/р | ||
| * — могут не вводиться при δ = 0;
** —– могут не вводиться и рассчитываться по зависимостям (3.37) и (3.38) | |||||
Поскольку зависимость термомеханических коэффициентов от степени и скорости деформации металла, от его температуры, а также зависимость предела текучести от последнего параметра в справочной литературе (например в [242]) в большинстве приводится в виде графиков (см. рис. 3.26) или таблиц, то вводить их рационально в виде аппроксимированных функций, например, вида:
 , (4.1)
, (4.1)
 , (4.2)
, (4.2)
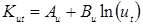 , (4.3)
, (4.3)
 , (4.4)
, (4.4)
для которых коэффициенты аппроксимации определяется по графическим или табличным справочным данным.
Третья группа исходных данных (табл. 4.1) характеризует в основном технологию и режим сварки. Поскольку известны способы точечной сварки как неизменными во время импульса тока параметрами усилия сжатия электродов (см. п.1.2.2), так и с изменяющейся их величиной по определенной программе [3, 54, 58, 253, 260, 261], то в последнем случае рационально их также задавать в виде аппроксимированных функций.
Практически любую известную в технологии точечной сварки программу изменения усилия сжатия токопроводящих электродов F Э t в процессе формирования соединения можно описать двумя степенными функциями изменения программированного параметра Р с одной точкой разрыва Bi в момент времени t 1 (рис. 4.2). В общем случае, для аппроксимации подобного изменения в процессе точечной сварки любого параметра Р функции можно записать следующим образом:
 , (4.5)
, (4.5)
 , (4.6)
, (4.6)
где АР, ВР и C Р — значения программируемого параметра в момент времени 0, t 1 и t СВ; a, b — показатели степени.
В случае, если изменение программируемого параметра Р t может быть описано одной функцией, то t 1 рационально принимать равным 0, т. е. изменение параметра Р t описывать в интервале времени t 1 … t СВ.
Коэффициенты аппроксимации АР, ВР, C Р, t 1, a, b, которые в этом случае определяются для программы изменения F Э в процессе КТС, водятся в исходных данных (табл. 4.2).
|
|
|
 Поскольку многие ошибки в исходных данных приводят к прерываниям вычислений (например, деление на нуль, логарифм отрицательного числа и т. п.), то рационально осуществлять их контроль после ввода (блок 3). Если обнаружена такая ошибка, то об этом выводится информация (блок 15) выполнение задачи прекращается.
Поскольку многие ошибки в исходных данных приводят к прерываниям вычислений (например, деление на нуль, логарифм отрицательного числа и т. п.), то рационально осуществлять их контроль после ввода (блок 3). Если обнаружена такая ошибка, то об этом выводится информация (блок 15) выполнение задачи прекращается.
В блоке 4 рассчитываются параметры, которые не зависят от времени [2]. Причем, в нем же осуществляется подготовка к выполнению циклов по времени t, в частности, определяется шаг расчета по времени Δ t = t СВ /п, где п — число шагов расчета, обнуляются требуемые переменные и задаются их начальное значения. Цикл по времени выполняется блоками 5...13 и заканчивается при выполнении заданного числа i шагов расчета.
Таблица 4.2
Исходные данные силового воздействия на детали при расчете диаметра уплотняющего пояска по уравнению (3.11)
| № пп | Параметры | Обозначение | Единица измерения |
| 1 | Неизменное усилие сжатия электродов | F Э | Н |
| 2 | Данные для аппроксимации программированного усилия сжатия электродов | А Р, В Р, CР, t1, a, b | б/р |
Вычисление диаметра пояска d П t в фиксированный момент t, осуществляется методом итераций путем последовательного приближения с уменьшением шага Δ d П (рис. 4.3). Поэтому в блоке 6 задается начальное значение d П t, равное диаметру ядра d Я t: d П t = d Я t. Это означает, что до начала плавления металла при t ≤ t НП начальное значение d П t = 0, а при t > t НП значение d П t задается равным d Я t.
 С блока 7 начинается участок алгоритма, осуществляющий цикл по диаметру уплотняющего пояска (блоки 8...11). В нем при каждом цикле по d П t его текущее значение изменяется на Δ d П. В блоке 8 последовательно осуществляются вычисления значений параметров термодеформационных процессов, которые заканчиваются расчетом усилия сжатия
С блока 7 начинается участок алгоритма, осуществляющий цикл по диаметру уплотняющего пояска (блоки 8...11). В нем при каждом цикле по d П t его текущее значение изменяется на Δ d П. В блоке 8 последовательно осуществляются вычисления значений параметров термодеформационных процессов, которые заканчиваются расчетом усилия сжатия 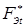 в площади уплотняющего пояска по уравнению равновесия (3.11), с учетом зависимостей (3.9) и (3.10), преобразованному к следующему виду:
в площади уплотняющего пояска по уравнению равновесия (3.11), с учетом зависимостей (3.9) и (3.10), преобразованному к следующему виду:
 , (4.7)
, (4.7)
где F Я t – усилие,развиваемое давлением жидкого металла в площади ядра; F П t – усилие в площади уплотняющего пояска; F Д t — усилие, необходимое для деформации деталей при их сближении до соприкосновения.
|
|
|
Горячая обработка металлов давлением производится, как правило, при температурах выше температуры рекристаллизации. Для этого интервала температур и определены в основном параметры сопротивления деформации материалов. Для области низких температур эти данные зачастую отсутствуют. Поэтому при расчетах с использованием параметров сопротивления деформации металла, его значения на область низких температур остается только экстраполировать. Однако для этих интервалов температур для большинства материалов известны зависимости от температуры их пределов текучести. Поэтому, при температурах материала, меньше которых не определены значения сопротивления деформации σ Д t (при T Д t < T σ), его значения рационально принимать равными пределу текучести σ Т t (блок 8). Это условие, при отсутствии значений сопротивления деформации, позволяет расчеты вообще производить по пределу текучести.
Использование в расчетах σ Д t и σ Т t оправдало двумя обстоятельствами. Во-первых, при сварке значения T Д t достигают значений T σ как правило за время t < 0,05…0,1 t СВ. Во-вторых, разница значений σ Д t и σ Т t быстро уменьшается по мере уменьшения жесткости режимов сварки и увеличения толщины свариваемых деталей.
Рассчитанное в блоке 8 значение усилие сжатия электродов 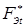 сравнивается с заданным F Э t (блок 9). Пока выполняется условие, что
сравнивается с заданным F Э t (блок 9). Пока выполняется условие, что  , цикл по d П t продолжается с тем же шагом Δ d П j переходом в блок 7. Если же это условие не выполняется, то есть
, цикл по d П t продолжается с тем же шагом Δ d П j переходом в блок 7. Если же это условие не выполняется, то есть 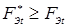 , то абсолютная разность между ними
, то абсолютная разность между ними 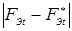 сравнивается с заданной погрешностью е F (блок 10). В случае, если
сравнивается с заданной погрешностью е F (блок 10). В случае, если  , то значение d П t уменьшается на Δ d П j, а Δ d П j уменьшается вдвое (блок 11) и осуществляется переход в блок 7, где d П t увеличивается на измененное значение Δ d П j и циклы по d П t продолжаются[3]. Если же
, то значение d П t уменьшается на Δ d П j, а Δ d П j уменьшается вдвое (блок 11) и осуществляется переход в блок 7, где d П t увеличивается на измененное значение Δ d П j и циклы по d П t продолжаются[3]. Если же  , то абсолютная разность между истинным значением диаметра уплотняющего пояска d П0 и расчётным d П i меньше или равна допускаемой погрешности е d:
, то абсолютная разность между истинным значением диаметра уплотняющего пояска d П0 и расчётным d П i меньше или равна допускаемой погрешности е d: 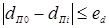 (см. рис. 4.3). На этом циклы по d П t заканчиваются и фиксируются результаты расчётов (блок 12). При условии, что i < n + 1 (блок 13), осуществляется переход в блок 5 и цикл по времени продолжается на следующем шаге расчета по t. После выполнения заданного числа шагов расчетов по времени t производится заданный вывод полученных результатов (блок 14) и решение задачи заканчивается.
(см. рис. 4.3). На этом циклы по d П t заканчиваются и фиксируются результаты расчётов (блок 12). При условии, что i < n + 1 (блок 13), осуществляется переход в блок 5 и цикл по времени продолжается на следующем шаге расчета по t. После выполнения заданного числа шагов расчетов по времени t производится заданный вывод полученных результатов (блок 14) и решение задачи заканчивается.
Диаметр уплотняющего пояска относится к тем немногочисленным параметрам процесса точечной сварки, которые можно легко измерить экспериментально. Вследствие этого, измеряя изменение диаметра уплотняющего пояска в процессе формирования соединения, представляется возможность оценить точность методики расчетов как диаметра уплотняющего пояска, так и обобщенно всех параметров термодеформационных процессов, используемых при решении уравнения (3.11).
|
|
|
Для проверки описанной выше термодеформационной модели процесса точечной сварки детали сваривали с прерываниями его в моменты ti (через 0,02 с) и измеряли полученный диаметр уплотняющего пояска. Для этих же условий сварки и моментов ti процесса формирования соединения производили расчет диаметра уплотняющего пояска d П t по описанной выше методике и сравнивали расчетные его значения с его величиной, измеренной экспериментально. Например, на рис. 4.4 показано изменение диаметра уплотняющего пояска в процессе формирования соединения, полученная экспериментально (кривая 1) и расчетом по описанной выше методике математического моделирования процесса КТС (кривая 2).
 Многочисленные сравнения расчетных и экспериментальных значений диаметра уплотняющего пояска показали, что их расхождения не превышает 5…15 %. Это, в определенной мере, отражает степень адекватности термодеформационной модели процесса формирования соединения и реального процесса точечной сварки, подтверждает приемлемость сделанных допущений и показывает допустимость использования данной модели для приближенных решений технологических задач КТС [206, 217].
Многочисленные сравнения расчетных и экспериментальных значений диаметра уплотняющего пояска показали, что их расхождения не превышает 5…15 %. Это, в определенной мере, отражает степень адекватности термодеформационной модели процесса формирования соединения и реального процесса точечной сварки, подтверждает приемлемость сделанных допущений и показывает допустимость использования данной модели для приближенных решений технологических задач КТС [206, 217].
|
|
|


