Оценка теплового состояния зоны сварки на стадии нагрева

 

Температура металла в зоне сварки является основным фактором, определяющим его сопротивление пластической деформации. Оно же, в свою очередь, через процессы микро- и макропластических деформаций определяет интенсивность процессов выделения и перераспределения теплоты и, в конечном итоге, размеры ядра расплавленного металла. Кроме того, нагрев вследствие дилатации металла, является активным фактором процесса макропластических деформаций при формировании соединения. В силу этого математическое моделирование изменения температурного поля при КТС является исходным условием разработки математических моделей других термодеформационных процессов. При этом анализ термодеформационных процессов на аналитических моделях становится возможным только в том случае, если математическая модель температурного поля удовлетворяет, по крайней мере, двум условиям: описывается непрерывной функцией; в достаточной степени точно отражает динамику его изменения в процессе формирования соединения.

Очевидно, что численные методы расчета температуры при КТС методами конечных разностей или конечных элементов (см. п. 2.4.2), хотя и наиболее точные в настоящее время, не удовлетворяют условию непрерывности функции. В аналитических моделях их иногда рационально использовать на стадии количественных расчетов.

Известные же аналитические методы, также приведенные в п. 2.4.2, как показывают сравнения расчетных и экспериментальных значений температуры, не удовлетворяют требованиям современных способов точечной сварки по точности получаемых результатов.

Вместе с тем, в теории и практике обработки металлов давлением для исследований термодеформационных процессов часто используют расчетно-экспериментальные методы. Анализ результатов исследований тепловых процессов в зоне точечной сварки показывает, что для исследований термодеформационных процессов в ряде случаев и при КТС допустимо использование подобных методов. При решении таких задач использование расчетно-экспериментального метода оценки теплового состояния зоны формирования соединения является компромиссным вариантом удовлетворения вышеуказанных условий. Причем, применительно к условиям точечной сварки их разработка облегчается такими свойствами процессов КТС, установленными рядом исследователей [73...76], как монотонность и подобие изменения параметров термодеформационных процессов при формировании точечных сварных соединений.

Ниже изложен метод оценки теплового состояния зоны формирования точечного сварного соединения на стадии нагрева (по содержанию типичный расчетно-экспериментальный) [214, 215], специально разработанный для аналитического моделирования термодеформационных процессов в условиях точечной сварки [206, 216].

3.3.1 Экспериментально - расчетный метод оценки теплового
состояния зоны сварки на стадии нагрева

Температурное поле при конкретных условиях формирования соединения и его изменение во время импульса сварочного тока можно описать функциями, аппроксимированными по экспериментально определенным характерным пространственно-временным точкам. Например, при точечной сварке относительно просто экспериментально можно определить ряд параметров температурного поля в зоне формирования соединения:

- изменение по времени и максимальную температуру в контакте электрод–деталь Т_Э;

- время t_НП, за которое температура в контакте деталь-деталь достигает значений температуры плавления Т_ПЛ свариваемого металла;

- изменение геометрического положения изотермы температуры плавления Т_ПЛ во времени (границы ядра расплавленного металла);

- температуру в контакте деталь-деталь Т_Д и температуру на границе уплотняющего пояска Т_П.

В общем случае, задача идентификации является задачей оценки параметров априорно заданной функции. Если тип нелинейной функции неизвестен, то аппроксимация истинной нелинейности может быть выполнена, например, с помощью полиномов. Однако во всех случаях идентификацию можно проводить только в предположении некоторого специфического типа нелинейной аппроксимирующей функции, параметры которой подлежат идентификации.

Для нахождения вида аппроксимирующих функций (рис. 3.5), которые с достаточной точностью отображали бы изменение температуры в плоскости оси электродов по координатам z (рис. 3.5, а) и r (рис. 3.5, б) для конкретного процесса сварки в любой его момент экспериментально можно определить значение температуры, по крайней мере, в четырёх характерных точках. По координате z:

- температуру Т_Э в контакте электрод-деталь (2 точки);

- температуру плавления Т_ПЛ по координатам границы (2 точки);

и по координате r:

- температуру плавления Т_ПЛ по координатам границы ядра (2 точки);

- температуру плавления Т_ПЛ по координатам границы ядра (2 точки);

Анализом имеющихся экспериментальных результатов и результатов, полученных расчетом температуры в зоне точечной сварки методом конечных разностей, установлено, что изменение температуры по координатам z и r (рис. 3.5) удовлетворительно описывается функцией вида

,                         (3.24)

где x — произвольная переменная; a и b — коэффициенты, которые можно определять по имеющимся экспериментальным значениям температуры.

Из анализа известных результатов экспериментальных и расчётных исследований можно сделать заключение о том, что изменение температуры по времени на стадии нагрева в любой точке зоны сварки подобно характеру изменения температуры в контакте электрод–деталь (рис. 3.6). При этом общеизвестно, что температура в контакте электрод–деталь в процессе сварки на стадии нагрева возрастает монотонно (рис. 3.6, а).

При точечной сварке непосредственное измерение температуры в контакте деталь–деталь и свариваемых деталях затруднено малыми размерами и закрытым характером зоны формирования соединения, а также быстротечностью процесса КТС. Вместе с тем, о характере изменения температуры в центре контакта деталь–деталь можно судить по трем характерным точкам, которые представляется возможным определить экспериментально (рис. 3.6, б):

- в начале процесса температура в центре контакта равна температуре окружающей среды (при t = 0 — Т _t = 0);

- в момент начала плавления t _НП она равна температуре плавления Т_ПЛ металла (при t = t _НП — Т _t = Т_ПЛ);

- в момент выключения сварочного тока t _СВ она достигает максимального Т _M значения (при t = t _СВ — Т _t = Т _M).

Приемлемую сходимость расчетных и экспериментальных значений температуры в интервале времени до начала плавления металла (0 ≤ t ≤ t _НП) позволяют получить показательная и логарифмическая функции вида:

и ,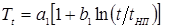

где a₁ и b₁ – коэффициенты, которые могут быть определены по имеющимся экспериментальным значениям температуры.

Однако при сварке на относительно жестких режимах, когда отношение t _НП / t _СВ = 0,15...0,3, а — Т_М/Т_ПЛ = 1,1...1,25, что обычно и имеет место при сварке на режимах средней жесткости, показательная функция в интервале t _НП … t _СВ имеет локальный максимум температуры, что противоречит имеющимся экспериментальным и расчетным данным о монотонном характере увеличения температуры во время действия импульса сварочного тока. Логарифмическая же функция не имеет этого недостатка. Поэтому она и была принята для описания изменения температуры по времени в первоначальном варианте данного экспериментально-расчетного метода [214], разработанном для условий КТС деталей из легких сплавов электродами со сферической рабочей поверхностью. Однако окончательные зависимости для расчетов параметров термодеформационных процессов при описании изменения температуры по времени логарифмической функцией получались неоправданно громоздкими [216]. Поэтому, в дальнейшем, при его совершенствовании применительно к особенностям сварки деталей из сталей электродами с плоской рабочей поверхностью, а также точечной сварки с обжатием периферийной зоны соединений, логарифмическая функция была заменена на степенную [210, 215, 217] вида:

,                                     (3.25)

где n и c – коэффициенты, которые подлежат идентификации.

Данная функция при указанных выше соотношениях t _НП / t _СВ и Т_М /Т_ПЛ не имеет локального максимума в интервале t _НП … t _СВ, хотя несколько и завышает значения температуры при t ≤ t _НП по сравнению с результатами, которые получаются при расчетах численными методами. Вместе с тем эксперименты показывают, что действительная скорость нарастания температуры в контакте деталь–деталь очень высока, так как следы оплавления на поверхностях деталей, по крайней мере, при сварке сталей, наблюдаются уже через один полупериод протекания сварочного тока. При относительной простоте степенная функция дает хорошую сходимость расчетных и экспериментальных результатов.

Разработка математической модели температурного поля по расчетно-экспериментальному методу, в сущности, сводится к определению и математическому описанию взаимосвязей аппроксимирующих функций (3.24), описывающих изменение температуры по координатам z и r, и функции (3.25), описывающей ее изменение по времени t.

При описании изменения температуры T_Zt по оси электродов (по координате z), в дискретный момент времени t, значения коэффициентов b и a в зависимости (3.24) применительно к конкретному процессу сварки можно найти, если представляется возможным экспериментально определить значения температуры в характерных точках в разные моменты процесса сварки. Для этого, предварительно для момента времени t преобразовав зависимость (3.24) к виду

,                               (3.26)

можно составить систему уравнений, учитывая, что при z = h _{Я t} /2 температура T_Zt = T _ПЛ, а при z = s — T_Zt = T _{Э t}:

 ,

где для момента времени t, h _{Я t} — высота ядра расплавленного металла;
T _{Э t} — температура на поверхности деталей под электродами; T _ПЛ — температура плавления свариваемого металла; s — толщина деталей.

Решив эту систему уравнений, находим значения коэффициентов b_t и a_Zt:

, ,

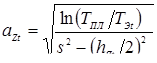подставив которые в (3.26) получим зависимость для расчета температуры T_Zt на оси электродов в точке с координатой z в момент времени t. После преобразований она будет иметь следующий вид:

.                      (3.27)

Эта зависимость имеет хорошую сходимость результатов при расчете изменения температуры по координате z, с результатами расчетов температуры численными методами, в частности, методом конечных разностей (рис. 3.7). Это, например, подтверждается на изменением температуры по оси электродов в момент выключения сварочного тока при сварке сплава АМг6 (рис. 3.7, а), рассчитанное по формуле (3.27) и методом конечных разностей в работе [165].

Для расчета в момент времени t изменения температуры T_rt по координате r зависимость (3.24) преобразуем к виду

.                               (3.28)

Определить коэффициенты  и а _rt можно аналогично тому, как определяли коэффициенты a_Zt и b_t, по известным значениям температуры T_rt в характерных точках (рис. 3.5, б): при r = d _{П t} /2 значение температуры T_rt на границе уплотняющего пояска равно T _П, то есть T_rt = T _П, при r = d _{Я t} /2 — T_rt = T _ПЛ и при r = 0 — T_rt = T _М.

Поскольку в точке с координатами  и  температура имеет максимальное значение T _М, то из зависимостей (3.27) и (3.28) можно записать следующее соотношение:

,

из которого можно определить коэффициент  для данных условий

,

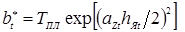а зависимость для расчета температуры по координате r можно записать следующим образом:

.

Поскольку на границе ядра расплавленного металла при  металл нагрет до температуры его плавления T _ПЛ, то из этой зависимости можно определить значение коэффициента а _rt, которое будет равно

.                                   (3.29)

Тогда зависимость для расчета изменения температуры по координате r в окончательном варианте имеет следующий вид

.                  (3.30)

Изменение температуры по координате r в момент выключения сварочного тока, рассчитанное по зависимости (3.30), также хорошо согласуется с результатами расчетов методом конечных разностей (рис.3.7, б).

 

Для расчетов изменения температуры в любой точке плоскости z – r зависимости (3.27) и (3.30) следует объединить. Это можно сделать, если учесть, что температурное поле неразрывно, а температура на оси электродов T_Zt при любом значении координаты z является максимальным значением температуры Т_М по координате r,т. е. при r = 0 значение T_Zt = Т_М. Из зависимостей (3.27) и (3.30) это соотношение температур по координатам z и r  можно выразить следующим образом:

.

Отсюда после преобразований получаем зависимость для расчета температуры в момент времени t в любой точке плоскости z – r в пределах зоны сварки, которая имеет следующий вид:

.           (3.31)

Характер изменения температурного поля по координатам z и r, рассчитанный по зависимости (3.31) в момент выключения сварочного тока, показан на рис. 3.8.

Зависимость (3.31) описывает изменение температурного поля в любой точке плоскости z – r только в отдельные дискретные моменты

времени t. Для анализа термодеформационных процессов в зоне сварки необходимо математически описать изменение температуры в каждой ее точке и по времени. Это можно сделать, если с зависимостью (3.31) функционально увязать зависимость (3.25), которая и описывает изменение тем

пературы по времени.

Определить значения коэффициентов n и c в зависимости (3.25) можно исходя из следующего.

В момент времени t _НП начала плавления металла в контакте деталь–деталь температура в точке с координатами z = 0и r = 0 равна значениям температуры плавления металла Т_ПЛ, т. е. при t = t _НП — T_t = Т_ПЛ. В момент же окончания импульса тока t _СВ температура в контакте деталь-деталь достигает максимальных значений Т_М, т. е. при t = t _СВ — T_t = Т_М. Это позволяет составить следующую систему уравнений

,

после решения которой и находим искомые коэффициенты n и c:

, .

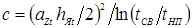Тогда зависимость для расчета изменения температуры в центре контакта деталь–деталь можно записать в виде

,                                    (3.32)

где с — коэффициент, определяемый для момента t = t _СВ, т. е. по конечной высоте ядра h _Я, и равный

,

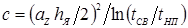где a_Z – значение коэффициента a_Zt, определяемого по зависимости (3.27) также для момента t = t _СВ, т. е. так же по конечной высоте ядра h _Я и максимальной температуре T _Э в контакте электрод–деталь:

.

Характер изменения температуры в центре свариваемого контакта, рассчитанный по зависимости (3.32) для различных условий сварки, показан на рис.3.9. Такое изменение температуры вполне согласуется с имеющимися данными, полученными как экспериментально, так и расчетами методом конечных разностей.

Выразим значение температуры плавления металла Т_ПЛ в формуле (3.32) через Т_М из формулы (3.31) при z = 0 и r = 0

и подставим это выражение в зависимость (3.32). Тогда эту зависимость можно преобразовать к следующему виду:

.                        (3.33)

Если допустить, что характер изменения температуры по времени от нуля до ее максимальных значений в любой точке зоны формирования соединения подобен характеру изменения температуры в центре контакта деталь–деталь, то значение Т_М в зависимости (3.33) равно значению Т _{z , r , t} рассчитанному по зависимости (3.31). Тогда зависимость (3.33) с учетом (3.31) и (3.29) можно преобразовать к следующему виду:

.                 (3.34)

Зависимость (3.34) описывает изменение температуры в зоне сварки на стадии нагрева по координатам z и r, а также по времени t при допущении, что характер изменения температуры по времени во всех точках зоны формирования точечного сварного соединения подобен характеру изменения температуры в центре контакта деталь–деталь.

Однако, в действительности, как показали расчеты температурных полей методом конечных разностей, характер изменения температуры по времени на периферии зоны сварки несколько иной, чем характер изменения температуры в центре контакта деталь–деталь. Это означает, что величина коэффициентов a_z и a_r, характеризующих градиент температуры по координатам z и r, должна изменяться по времени и зависеть от условий сварки, в частности, от формы рабочей поверхности электродов.

Проведенные исследования показали, что изменение значений коэффициентов a_z и a_r может быть аппроксимировано функцией вида [217]

,                          (3.35)

где a_t и a – текущие и конечные значения коэффициента a_z или a_r при их изменении по времени; т и п – экспериментально определяемые коэффициенты аппроксимации.

Тогда окончательно формулу для расчета изменения температуры в любой точке зоны сварки в любой момент времени в интервале 0 < t ≤ t _СВ с учетом сказанного выше можно представить в следующем виде:

,                        (3.36)

где t — координата времени; c, a_zt и a_rt – коэффициенты, характеризующие изменение в процессе сварки градиента температуры по цилиндрическим координатам z и r и времени t:

,            ,           ,

,       ;

Т_Э — максимальное значение температуры в контакте электрод–деталь;
t _НП — время начала плавления металла в контакте деталь–деталь; m ₁, n ₁, m ₂ и n ₂ — опытные коэффициенты, учитывающие изменение во времени градиента температуры по координатам z и r (см. ниже табл. 3.2).

Известные трудности при расчетах температуры по зависимости (3.36) представляет точное определение для конкретных условий сварки момента начала плавления металла в контакте деталь–деталь t _НП, максимальной температуры в контакте электрод–деталь Т_Э, а также коэффициентов m ₁, n ₁, m ₂ и n ₂, которые учитывают изменение во времени градиента температуры по координатам z и r. Несомненно, что при решении научно-исследовательских задач они в каждом конкретном случае должны определяться индивидуально. При приближенных технологических расчетах они могут быть определены по приведенным ниже обобщенным данным.

Наиболее просто определять момент t _НП начала плавления металла в контакте деталь–деталь. Это можно осуществить прерыванием процесса сварки (на серийных машинах это можно сделать с шагом 0,02 или 0,01 с). Установлено, что с увеличением жесткости режима сварки момент начала плавления металла t _НП смещается к началу процесса и существует корреляционная зависимость между значением t _НП и проплавлением деталей, выраженным отношением высоты ядра расплавленного металла к суммарной толщине деталей h _Я /2 s. Усредненная для способов КТС зависимость значений t _НП от проплавления деталей h _Я /2 s, показанная на рис. 3.10, вполне удовлетворительно описывается функцией, интерполированной по полиному Лагранжа [217]:

, (3.37)

где t _СВ – время сварки; h _Я – высота ядра; s –толщина детали.

Экспериментальное определение максимального значения температуры в контакте электрод-деталь Т_Э не имеет принципиальных препятствий. Этоможно сделать по любой из известных методик, например, описанным в работах [14, 207]. Основная трудность таких измерений — это их относительно большая трудоемкость.

Проведенными исследованиями и обработкой известных результатов экспериментов других исследователей, а также результатов расчетов температуры методом конечных разностей, установлено наличие корреляционной зависимости между максимальным значением температуры в контакте электрод–деталь Т_Э и относительным проплавлением деталей h _Я / 2 s (рис. 3.10). Зависимость  удовлетворительно описывается следующей, относительно простой, аппроксимированной функцией:

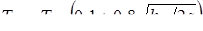,                           (3.38)

где Т_ПЛ — температура плавления металла; h _Я — высота ядра; s —толщина свариваемых деталей.

Наиболее трудоемко определение изменения в процессе формирования соединения коэффициентов a_zt и a_rt, характеризующих изменение градиента температуры по координатам z и r. Для этого необходимо измерять значения температуры в характерных точках (см. рис. 3.5), а затем определять значения a_zt и a_rt обратным расчетом по зависимости (3.36). Трудоемкость определения этих коэффициентов можно несколько уменьшить после начала плавления металла. Для этого экспериментально следует измерять изменение высоты h _{Я t} и диаметра d _{Я t} ядра, а коэффициенты a_zt и a_rt так же определять обратным расчетом по зависимостям (3.40) и (3.41). Обработкой значительного числа экспериментальных данных установлено, что характер изменения коэффициентов a_zt и a_rt в процессе формирования точечных сварных соединений зависит в основном от геометрии рабочей поверхности электродов и жесткости режимов сварки.

Наиболее близкий характер изменения градиента температуры по координатам z и r в процессе формирования соединения при сварке электродами со сферической рабочей поверхностью (рис. 3.11). При сварке электродами со сферической рабочей поверхностью плавление металла начинается в относительно небольшом объёме и увеличение высоты h _{Я t} (рис. 3.11, а) и диаметра d _{Я t} (рис. 3.11, б) ядра происходит плавно. Это обусловлено тем, что градиент изменения температуры по координатам z и r в начале процесса нагрева весьма высок, а в процессе сварки плавно уменьшается, вследствие чего уменьшаются и значения коэффициентов a_zt (рис. 3.11, а) и a_rt (рис. 3.11, б).

Изменения градиента температуры по координатам z и r в процессе формирования соединения при сварке электродами с плоской рабочей поверхностью различаются в большей степени, в особенности в начале процесса сварки (рис. 3.12).
При сварке электродами с плоской рабочей поверхностью плавление металла начинается по большей площади контакта, чем при сварке электродами со сферической рабочей поверхностью, что обусловлено меньшим градиентом температуры по координате r. Затем, увеличение высоты h _{Я t} (рис. 3.12, а) и диаметра d _{Я t} (рис. 3.12, 6) ядра также происходит плавно. Градиент изменения температуры по координате z изменяется аналогично предыдущему, соответственно изменяется и a_zt (рис. 3.12, а). Отличия носят лишь количественный характер. Градиент же изменения температуры по координате r в процессе сварки, в отличие от предыдущего случая, почти не изменяется, хотя в начальной стадии наблюдается повышенный его разброс. Это предопределяет относительно большие начальные значения диаметров ядра (рис. 3.12, б) и относительно не большие изменения значений a_rt (рис. 3.12, б).

При точечной сварке с обжатием периферийной зоны соединения плавление металла начинается по еще большей площади контакта, чем при сварке электродами с плоской рабочей поверхностью (рис. 3.13).

Затем, увеличение высоты h _{Я t} (рис. 3.13, а) и диаметра d _{Я t}
(рис. 3.13, б) ядра также происходит плавно. Градиент изменения температуры по координате z изменяется аналогично предыдущим случаям, соответственно изменяется и a_zt (рис. 3.13, а). Отличия носят лишь количественный характер. Градиент же изменения температуры по координате r, в отличие от предыдущих случаев, в начале процесса сварки меньше чем в конце и монотонно возрастает в процессе формирования соединения. Это предопределяет несколько большие начальные значения диаметров ядра (рис. 3.13, б) и увеличение значений a_rt в процессе сварки (рис. 3.12, б).

Конечно, полученные таким образом значения коэффициентов a_zt и a_rt весьма приближённы, но, как показали сравнения расчётных и экспериментальных значений температуры и размеров ядра, приемлемы для решения приближенных технологических задач. Для практических расчетов полученные значения коэффициентов a_zt и a_rt обобщены аппроксимированными функциями, описывающими их изменение в процессе формирования соединений (зависимости (3.35) и (3.36)). Значения коэффициентов m ₁, n ₁, m ₂ и n ₂, необходимые для расчетов температуры в зоне формирования соединения по данному расчетно-экспериментальному методу, для различных условий сварки обобщены в табл. 3.2 [215, 217].

Таблица 3.2

Значения коэффициентов m ₁, n ₁, m ₂ и n ₂ для расчетов температуры в зоне формирования соединения при различных условиях сварки

Условия точечной сварки	Значения коэффициентов*)
	m 1	n1	m2	n2
Электродом со сферической рабочей поверхностью	1,9...2,1	0,5...0,7	1,4...2,1	0,5...0,7
Электродом с плоской рабочей поверхностью	1,6...1,9	0,35...0,45	1,9...2,1	0,45...0,55
С обжатием периферии сварной точки	1,2...1,8	0,25...0,35	0,05...0,8	0,35...0,45
*) Большие значения относятся к более жестким режимам

 

Изменение температуры в процессе КТС в различных точках зоны сварки, рассчитанное по данному расчетно-экспериментальному методу, в частности, в центре контакта деталь–деталь, в контакте электрод–деталь вполне согласуется с имеющимися данными, полученными экспериментально (осциллографированием) и расчетами методом конечных разностей и конечных элементов (рис 3.14).

Так, температура в центре контакта деталь–деталь (кривая 1) быстро, за время равное 0,1...0,2 t _СВ, нарастает до температуры, близкой к температуре плавления, а затем рост температуры замедляется. Причем изменение температуры в центре контакта деталь–деталь, рассчитанное по формулам (3.34) и (3.36) совпадает. Это объясняется тем, что она не зависит от координат, т. е. градиента температуры в зоне сварки, и фактически определяется зависимостью (3.33). Изменение же температуры в контакте электрод–деталь, рассчитанное по зависимости (3.36) (кривая 2), ближе к экспериментальным результатам (кривые 3), чем рассчитанное по зависимости (3.34) (кривая 4), поскольку она учитывает различия градиента температуры в разных точках зоны сварки.

Температурное поле в зоне сварки по координатам и времениотличается весьма высоким градиентом температур (рис. 3.15).

Характер изменения температурного поля по координатам и времени вполне соответствует имеющимся данным, полученным как экспериментально, так и решениями дифференциальных уравнений методами конечных разностей и конечных элементов.

3.3.2 Методики расчетного определения размеров ядра и средних
значений температуры в зоне сварки

При решении большинства технологических задач КТС, в частности определения силовых параметров режимов сварки, возникает необходимость в расчетном определении размеров ядра (как правило, его диаметра и высоты) и средних значений температуры в определенных участках зоны формирования соединения.

Размеры ядра расплавленного металла можно определить по положению изотермы температуры плавления, в частности, высоту h _{Я t} и диаметр d _{Я t} ядра можно определить по координатам пересечения изотермы температуры плавления Т_ПЛ с координатными осями z и r. Положение изотермы любой температуры в зоне формирования соединения в любой момент времени можно определить из зависимости (3.36), если значение температуры изотермы Т_И подставить в ее левую часть. После преобразований получаем выражение:

,            (3.39)

которое является общеизвестным [208] уравнением эллипса, но только с изменяющимися по времени полуосями.

Например, расположение изотерм (рис. 3.16), показанных сплошными линиями и рассчитанных по зависимости (3.39) для тех же условий сварки, для которых они рассчитывались в работе [165] решением дифференциальных уравнений методом конечных разностей (пунктирные линии), почти совпадают между собой. В частности, в приведенном примере положение изотермы Т_И = 600 ºС показывает контур ядра расплавленного металла (температура плавления Т_ПЛ сплава АМг6 ~ 623 ºС). Причем изотерма Т_И = 600 ºС, рассчитанная по зависимости (3.39), в большей мере совпадает с контуром ядра, определённым по макрошлифу. Это объясняется тем, что расчетно-экспериментальный метод закладываются конечные размеры (высота h _Я и диаметр d _Я) ядра. Таким образом, при Т_И = Т_ПЛ зависимость (3.39) описывает контур ядра расплавленного металла:

.

Поскольку полуоси эллипса изотермы температуры плавления равны половине высоты  и диаметра  ядра, то по этой зависимости можно определить их значения в любой момент времени t процесса формирования ядра. После преобразований получены формулы для расчета высоты h _{Я t} и диаметра d _{Я t} ядра в любой момент времени t после начала плавления металла (времени t _НП, которое можно определить по зависимости (3.37)) до окончания импульса сварочного тока (при t _НП < t ≤ t _СВ) [217]:

,                                (3.40)

,                                (3.41)

где a_zt и a_rt — коэффициенты, характеризующие изменение градиентов температуры по координатам z и r, которые можно определить по зависимости (3.36) с использованием данных табл. 3.2.

Изменение высоты и диаметра ядра в процессе его формирования, рассчитанные по формулам (3.40) и (3.41), вполне согласуются с данными, полученными из практики КТС (рис. 3.17). Данные формулы дают удовлетворительную сходимость расчетных и экспериментальных результатов (показаны точками), расхождение которых не превышает ± 10 %.

Среднюю температуру по одной из координат z или r, или же по участку плоскости z — r в момент времени t можно определить из зависимости (3.36), используя общеизвестную [208] теорему о среднем, согласно которой средняя температура по координатам z или r на участках z ₂ – z ₁ или r ₂ – r ₁, а также по элементу площади S _{П t} в плоскости z — r, может быть выражена следующими зависимостями:

,

,

.

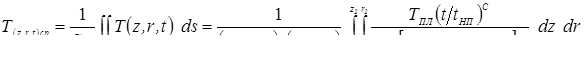Точные вычисления средних значений температуры в зоне сварки по приведенным выше зависимостям невозможны из-за того, что интегралы вида , которые содержатся в вышеуказанных зависимостях, при четных значениях n аналитически не вычисляются [208]. В таких случаях, как правило, подобные интегралы путем подстановок сводят к интегралам, значения которых вычислены приближенными методами. Для данного случая наиболее подходящим из вышеуказанных является интеграл вида erf (y), который называют erf -функцией или функцией ошибок. Его табличные значения приведены справочниках, например, в [208].

После подстановок, вычисления интегралов и преобразований зависимости для количественных расчетов средних значений температуры в зоне сварки по координатам z или r, а также по площади S _{П t} в плоскости
z — r, имеют следующий вид:

,   (3.42)

,          (3.43)

,  (3.44)

где для момента времени t, Т_{( z , t )ср} — средняя температура по координате z на участке z ₂ – z ₁ при любом значении r; Т_{( r , t )ср} — средняя

Предыдущая10111213141516171819202122232425Следующая

Поделиться:

Воспользуйтесь поиском по сайту: