 |
Умножение на пальцах рук на 6, 7, 8
|
|
|
|
Умножение на пальцах рук на 6, 7, 8
Поверните кисти рук ладонями к себе. Каждому пальцу, начиная с мизинца, присвойте цифры от 6 до 10.
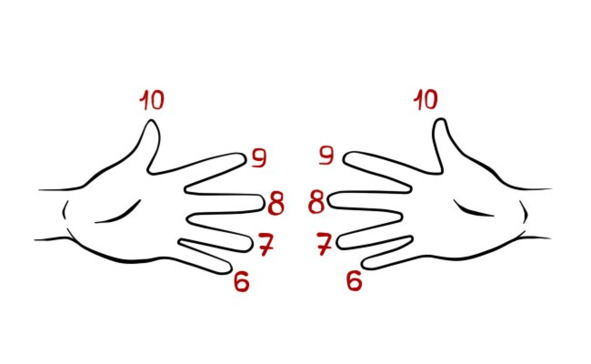
Теперь таким же образом попробуйте умножить 7 на 8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.

Пальцы левой руки, оставшиеся сверху, умножьте на пальцы правой руки, — это и будут единицы (3 х 2=6).
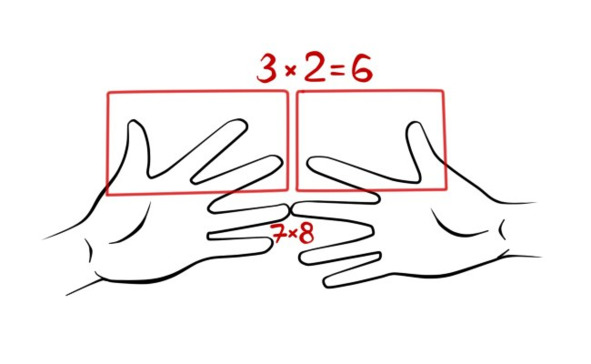
Теперь сосчитайте пальцы: количество пальцев под соединенными пальцами — это десятки.
Итог равен 56.
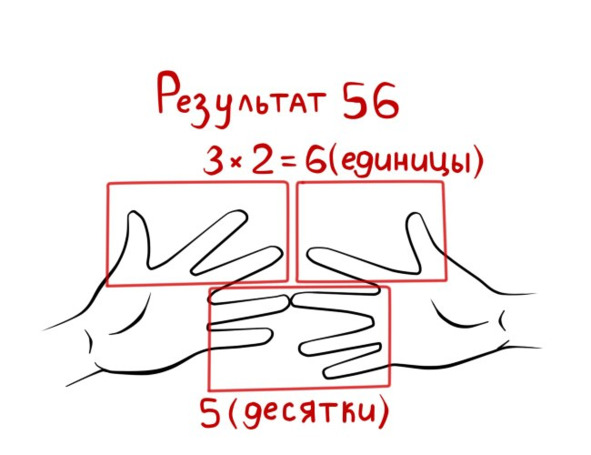
Если при умножении «единиц» результат получается больше 9, то оба результата нужно плюсовать в столбик.
Например, если нужно 7 умножить на 6.
В этом случае «единицы» равны 12 (3 х 4). А десятки равны 3.
3 (десятки)
+
12 (единицы)
________
Интересных приемов можно найти и больше, главное, чтобы они помогли именно вашему ребенку запомнить сложные для него примеры таблицы умножения.
Техника №23. Стихи про таблицу умножения
Стихотворения для запоминания сложных примеров таблицы умножения можно сочинить самим или найти в интернете.
Например:
Свинка свинёнка решила проверить:
— Сколько получится девять на девять?
— Восемьдесят — хрю — один! —
Так ответил юный свин.
У семи матрёшек
Вся семья внутри:
Семью девять крошек —
Шестьдесят три.
И конечно, поиграйте!

Техника №24. «Пазлы»
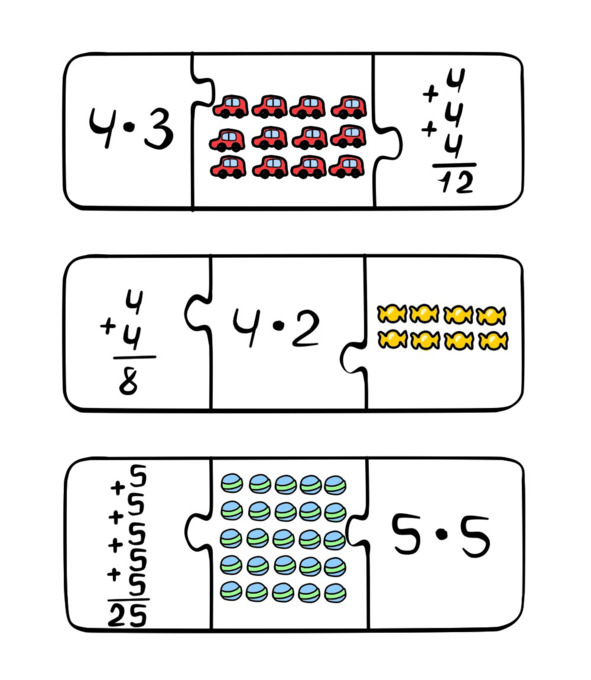
На сложные примеры, которые вы «отловили» на шаге пять, можно составить карточки-пазлы.
Они помогут еще раз разложить «по полочкам» смысл действия умножения и запомнить пример.
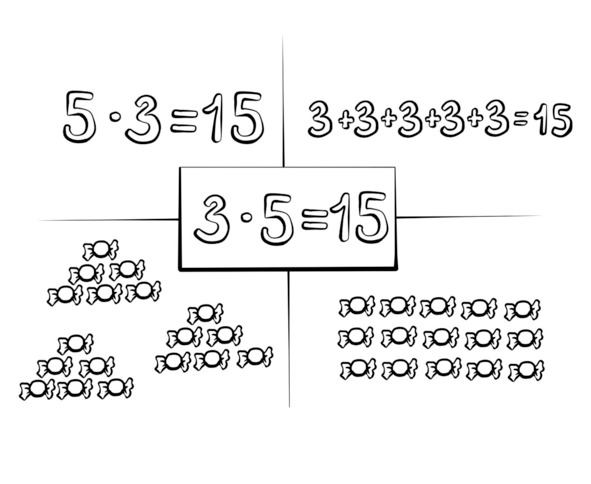
В данной карточке показаны:
— переместительный закон умножения;
— смысл действия умножения;
— результат умножения.
А для повторения таблицы умножения заполните гусеницу, записав в нее таблицу умножения чисел:
|
|
|

Техника №25. «Робот» для объяснения дробей
Как эффективно объяснить ребенку дроби?
Шаг первый — ввести понятие «доли».
Детям показывают апельсин и предлагают разделить его на доли.
Один апельсин — это целый предмет. И состоит он из долей.
На доли можно поделить многое: арбуз, яблоко, шоколад и даже квартиру (комната, кухня, коридор — все это доли квартиры).
Будет замечательно, если ребенок и вы возьмете и физически разделите шоколадку на доли, апельсинку на доли, мандаринку на доли.
Именно на этом шаге мы обращаем внимание на то, что один апельсин — это целый предмет, и его можно обозначить цифрой 1.
Шоколадка — целый предмет, или 1 шоколадка.
Вторым шагом необходимо ввести понятие «дробь».
Ведь мы шоколадку «разделили» или «раздробили» на части! Апельсин разделили или «раздробили» на доли!
Хорошим подспорьем являются детали ЛЕГО, из которых можно собрать целый прямоугольник и «раздробить» его на части.
На этом шаге можно нарисовать прямоугольник, разделить его на 4 равные части, например, и попросить ребенка закрасить (или отделить) одну часть, две части.
Нарисовать квадрат, раздробить его на 4 части. И попросить закрасить 2 части.
Шаг три — научить ребенка записывать часть.
Передаем инициативу думать и делать выводы ребенку и задаем ему вопрос.
— Кто догадается, сколько всего частей в этом предмете?
— На сколько частей мы его раздробили? Разделили?
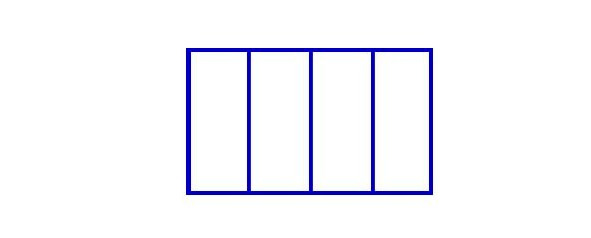
На четыре!
Вспоминаем, что деление (при делении в столбик, записывается чертой).
Так же и в дробях. Черта обозначает деление! На сколько частей мы разделили данный прямоугольник?
Так и напишем, делили на 4:

А давай возьмем две части? Как закрасим? Как напишем?
Далее необходимо разделить прямоугольник на другое количество частей и предложить взять две части. Спросите ребенка, как это показать.
|
|
|

Как записать, что взяли 2 части из 4?
Вспоминаем, что надо поставить черту (разделить), на 4 части. И взять 2 части.
Шаг 4 — переходим к записи целой части через дробь.
Для этого шага пригодится шоколадка. Можно спросить, сколько шоколадок. Одна.
— На сколько долек мы раздробили шоколадку?
— На 8 долек.
— Как записать шоколадку, но с помощью дроби? На сколько разделили?
— На 8 частей.
— А в целой сколько частей?
8 частей или 8/8 целая шоколадка.
Далее возвращаемся и записываем целым предметом другие разделенные до этого предметы.
Шаг 5 — практика.
Отломите три кусочка, дайте ребенку. Сколько дали? 3. От скольки? от 8!
Запишем полученную дробь 3/8!
Детали лего, полоски, прямоугольники, шоколад, конфеты, жвачки с дольками и т. п.
В ход идет любой подручный материал.
Но одно условие — дробить надо на равные части.
Дети очень любят играть с дольками из пачки жвачки.
10/10 — это целая упаковка жвачки.
2/10 — как в рекламе.
6/10 — 6 долек из пачки жвачки.
Здесь прекрасным помощником будет робот:
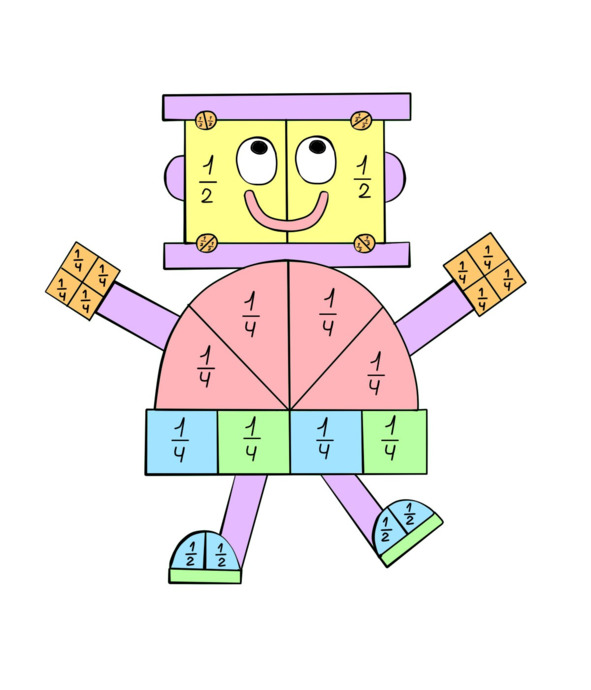
Шаг 6 — разбираемся в терминологии.
И снова задаем ребенку вопросы и помогаем найти ответы.
— В числе 3/8 что обозначает число 8?
— На сколько поделили.
— Что означает число 3?
— Сколько взяли!
— Правильно, число долек, которое взяли. Его еще называют числитель.
Шаг 7 — задачки с подвохом.
Предложите ребенку две дроби:
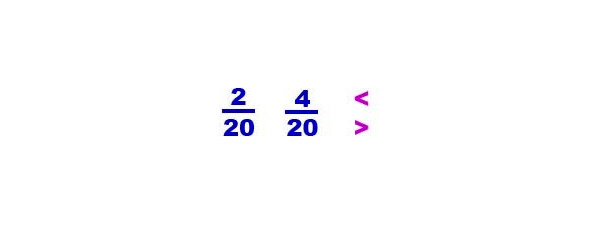
И поставить знак> в ту сторону, какая дробь больше.
Для выполнения задания лучше взять шоколадку, в которой есть 20 долек.
И взять 2 дольки (приложить к дроби 2/20) и 4 дольки (приложить к дроби 4/20). Спросить, где больше, глядя куда ворона откроет рот.
Техника ворона, благодаря которой детям можно объяснить тему сравнения чисел представлена в видео ниже:
Когда ребенок справится с этим заданием и подобными, усложняем задачу.
Пишем другой пример.
Вспоминаем шоколадку.
Взяли и там и там по две части. Но в первом случае, раздробили шоколадку на 20 долек, а во втором — эту же шоколадку, на 10 долек.
|
|
|
Конечно, лучше всего проделать это на практике.
Подобные сравнения — самая сложная тема для детей на этапе знакомства с темой дроби. Им кажется, что если число 20 больше, то и дробь тоже.
И именно здесь скрывается подводный камень.
Попробуйте и практикуйте с шоколадкой такие примеры.
Ребенок при соблюдении последовательности шагов при объяснении темы, а также если вы не будете давать готовые решения и ответы, схватит тему и поймет ее.
А именно это является самым ценным.
Такой подход называется проблемным обучением, или развитием в ребенке критического мышления: когда мы ребенку не даем правило или ответ, но помогаем вывести его самому.
Ведь ребенок сам назвал, что шоколадку «раздробили», а значит, узнал слово «дробь».
Сам вспомнил, как записывать деление чертой.
Сам ответил, что в примере 3/8 тройка — это число долек, которые «взяли», числитель.
Сам понял, что 8 — это на сколько поделили.
Практика в сочетании с правильной методикой обучения творит чудеса!
|
|
|


