 |
1. Векторы. Действия над векторами.
|
|
|
|
1. Векторы. Действия над векторами.
Вектором наз. упорядоченная совокупность чисел Х={X1, X2,... Xn} вектор дан в n-мерном пространстве. Т(X1, X2, X3). n=1, 2, 3. Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.
1. умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А||В. б) l> 0, то АВ, l< 0, то А¯ В. в)l> 1, то А< В, )l< 1, то А> В. 2. Разделить вектор на число n значит умножить его на число, обратное n: а/n=a*(1/n).
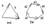3. Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а.
2. 3. Декартова прямоугольная система координат. Базис.
Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.
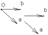Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.
Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.
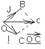ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х, у наз-ся координатами вектора ОС в данном базисе
4. Действия над векторами.
а=х1i+y1j+z1k; b=х2i+y2j+z2k
l*a=l(х1i+y1j+z1k)= l(х1)i+l (y1)j+l(z1)k
a±b=(x1±x2)i+(y1±y2)j+(z1±z2)k
ab=x1x2ii+y1x2ij+x2z1ki+x1y2ij+y1y2jj+ z1y2kj+x1z1ik+y1z2jk+z1z2kk=x1x2+y1y2+z1z2
ii=1; ij=0; и т. д.
скалярное произведение 2х векторов равно сумме произведений соответствующих координат этих векторов.
|
|
|
аа=x2+y2+z2=|a|2 a{x, y, z}, aa=|a|*|a|, то a2=|a|2
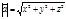
ab=|a|*|b|*cosj
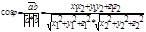
а)ав=0, < => а^в, x1x2+y1y2+z1z2=0
б)а||в - коллинеарны, если, x1/x2=y1/y2=z1/z2
5. Скалярное произведение векторов и его свойства.
-(“skala”-шкала) 2х векторов а и в наз. число, равное произведению длин этих векторов на cos угла между ними. (а, в)- скалярное произведение. а*в=|а|*|в|*cosj, j=p/2, cosp/2=0, a^b=> ab=0. Равенство “0” скаляргного произведения необходимое и достаточное условие их перпендикулярности (ортогональности).
6. Векторное произведение 2х векторов.
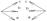
левая ----- правая
Тройка векторов а, в, с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки - левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям: 1. |c|=|a|*|b|*sinj. 2. c^a и c^b. 3. тройка а, в, с-правая.
7. Смешанное произведение векторов и его свойства.
Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a*b*c=[a*b]*c=a*[b*c], где
a={ax, ay, az}
b={bx, by, bz}
c={cx, cy, cz}
Св-ва:
1. При перестановке 2х сомножителей:
a*b*c=-b*c*a
2. не меняется при перестановке циклических сомножителей:
a*b*c=c*a*b=b*c*a
3. а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a*b*c=0
б)если некомпланарные вектора a, b, c привести к 1 началу, то |a*b*c|=Vпараллепипеда, построенного на этих векторах
если a*b*c> 0, то тройка a, b, c - правая
если a*b*c< 0, то тройка a, b, c - левая
8. Уравнение линии и поверхности.
1. Уравнение сферы. Сфера- геометрическое место точек, равноудаленных от 1ой точки, называемой центром.
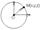O(a, b, c)
|OM|=r, OM={x-a, y-b, z-c}
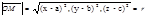
r2=(x-a)2+(y-b)2+(z-c)2- уравнение сферы. x2+y2+z2=r2- ур-е сферы с центром точке(0, 0).
F(x, y, z)=0- ур-е поверхности - ур-ю, удовлетворяющему координатам x, y, z любой точки, лежащей на поверхности.
|
|
|
2. Уравнение окружности
|OM|=r, OM={x-a, y-b)
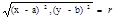
r2=(x-a)2+(y-b)2+(z-c)2- ур-е окружности
а=b=0, то x2+y2=r2
F(x, y)=0- ур-е линии на плоскости.
|
|
|
