 |
54. Экстремумы ф-ций. Признаки существования экстремума. Наибольшее и наименьшее значение ф-ции 1й переменной.
|
|
|
|
54. Экстремумы ф-ций. Признаки существования экстремума. Наибольшее и наименьшее значение ф-ции 1й переменной.
Точка х называется точкой max ф-ции, если значение ф-ции в этой точке - наименьшее в некоторой ее окрестности.
1- локальный max
2- локальный min
3- глобальный max
4- глобальный min
если tga> 0, то f`(x)> 0
если tga< 0, то f`(x)< 0
Необходимый признак экстремума: ф-ия f(x) может иметь max и min только в тех точках, в которых f`(x)=0 или не существует.
 (В них можно построить ¥ касательных).
(В них можно построить ¥ касательных).
Достаточный признак: точка х0 является точкой экстремума, если ее производная в этой точке меняет знак:
- если с “+” на “-”, то х0- т. max
- если с “-” на “+”, то х0- т. min
55. Выпуклость и вогнутость линий точки перегиба.
Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках.
Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.
Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.
Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная < =0; если линия на интервале вогнутая, то ее f``(x)> =0
Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)> 0, то линия вогнутая
Признаки точки перегиба: чтобы X0 была т. перегиба, < => чтобы у`` в этой точке = 0 и меняла знак при переходе х через х0.
56. Асимптота графика ф-ции.
Асимптота - прямая, к которой график ф-ции стремится, но никогда ее не пересекает.
1) прямая х=х0 назыв-ся вертикальной асимптотой графика ф-ции f(x)=y, если при х®х0 |f(x)|®+¥ (вида x=b)
2) y=kx+b, , y=f(x) - общее ур-е наклонной асимптоты
|
|
|
lim[f(x)-(kx+b)]=0, f(x)=kx+b+a(б. м. в. ) по св-ву x®¥ пределов.
разделим левую и правую части на х. Возьмем предел при х®¥
f(x)/x=k+b/x+a/x, lim(f(x)/x)=limk+lim(b/x)+lim(a/x)
x®¥
, то
k=lim(f(x)/x)
b=lim[f(x)-kx]
Если эти пределы существуют, то существует и наклонная ассимптота вида kx+b=y
3)k=lim(f(x)/x)=0, y=b - горизонтальная асимптота.
57. Предел и непрерывность ф-ции нескольких переменных.
Величина U наз-ся ф-цией переменных (x1, x2... xn), если каждой, рассматриваемой в совокупности этих величин соотв-ет 1 определенное значение величины U.
Пусть f(M)=M0(x10, x20,... xn0), M(x1, x2,... xn)
Ф-ция f(M)=f(x1, x2,... xn) имеет предел А при М0®М, если каждому значению как угодно малого числа d(дельта) соотв-ет, как угодно малое заданное число e> 0, если |M0M|=d, то |f(M)-A|< e
Ф-ция f(M) наз-ся непрерывной в точке М0, если б. м. приращению любого аргумента соответствует б. м. приращение ф-ции.
limf(x10, x20,... xn0)=limf(x1, x2,... xn)
x10 ® x1
x20 ® x2
xn0 ® xn
58. а) Частная производная ф-ции нескольких переменных. б) Частный и полный дифференциалы.
а) рассмотрим на примере ф-ции 2х переменных
x=f(x, y), точка A(x0, y0)
Dz=f(x0+Dx, y0+Dy)-f(x0, y0) - полное приращение.
Частное приращение по х (по у):
DxZ=f(x0+Dx, y)-f(x0, y0)
DyZ=f(y0+Dy, x)-f(x0, y0)
Частная производная ф-ция:

 б) dxZ=Zx`*Dx=¶Z/¶x*dx; dxZ=Zy`*Dy=¶Z/¶y*dy
б) dxZ=Zx`*Dx=¶Z/¶x*dx; dxZ=Zy`*Dy=¶Z/¶y*dy
Полный дифференциал dZ=dxZ+dyZ=Z`xdx +Z`ydy
dZ=¶Z/¶x*dx+=¶Z/¶y*dy
Чтобы найти полный дифференциал ф-ции надо найти частные производные от этой ф-ции по всем независимым переменным, умножить их на дифференциал этих переменных, рез-ты сложить.
59. Производная 2го порядка ф-ции нескольких переменных. Дифференцирование сложной ф-ции 2х переменных.
Частное производной 2го порядка от ф-ции Z явл. частная производная от 1й производной:
Z``XX=(Z`x)`x; Z``yy=(Z`y)`y
Z``Xy=(Z`x)`y=(Z`y)`x


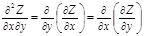
60. Экстремумы ф-ции нескольких переменных. Необходимые и достаточные признаки экстремума ф-ции 2х переменных.
|
|
|
Z=f(x, y), M0(x0, y0), M(x, y)
Max ф-ции Z называется такое ее значение f(x0, y0), которое является наибольшим среди всех значений, принимаемых в некоторой окрестности точки M0
Min ф-ции Z называется такое ее значение f(x0, y0), которое является наименьшим среди всех значений, принимаемых в некоторой окрестности точки M0
Экстремум сущ. в тех точках, в которых частная производная ф-ции Z=0 или не существует:

Если Z=f(x1, x2,... xn), то ¶Z/¶xi=0, i=1, 2,... n - необходимое условие.
Достаточный признак:

где A= Z``XX(x0, y0), C= Z``yy(x0, y0), B= Z``yx (x0, y0),
1) если D> 0, то М0 - точка экстремума;
если А< 0 или С< 0, то М0 - точка max;
если А> 0 или С> 0, то М0 - точка min.
2) если D< 0, то экстремума нет
3) если D=0, то вопрос о существовании экстремума остается открытым.
|
|
|


