 |
34. Признаки существования а) предела ф-ции и б) предела последовательности.
|
|
|
|
34. Признаки существования а) предела ф-ции и б) предела последовательности.
а) если все значения ф-ции f(x) заключены между значениями ф-ции j(x) и g(x), которые имеют 1 предел при х®а, то и limf(x)=A
j(x)< =f(x)< =g(x), где limj(x)=А, limg(x)=А, то limf(x)=A. х®а
б) Если последовательность монотонно возрастает и ограниченна сверху, то она имеет предел.
Последовательность монотонно возрастает, если последующий член> предыдущего (xn+1> xn)
Последовательность ограничена сверху, если существует такое М, что xn< =M.
35. Бесконечно малые величины и их св-ва:
величина называется б. м. в. в каком-то процессе, если она в этом процессе бесконечно уменьщается. (r=m/V, если V®¥, то r®0)
Св-ва б. м. в.:
-сумма или разность конечного числа б. м. в. есть б. м. в. (a и b-б. м. в., то a±b=б. м. в. )
-произведение б. м. в. на величину ограниченную есть б. м. в. (U< =M, то a*U=б. м. в. )
-произведение б. м. величин=б. м. в.
-произведение б. м. в. на постоянную = б. м. в
36. Бесконечно большие величины и их св-ва.
б. б. в - величина для которой |Xn|®¥ (при xn=1/n, n®0, то xn®¥ )
Св-ва:
-величина обратная б. б. в. явл. б. м. в. (1/¥ =0; 1/0=¥ )
-сумма б. б. в. (с одинаковым знаком) есть б. б. в.
-произведение 2х б. м. величин=б. м. в.
-частное от деления 2х б. б. в = неопределенность
38. Св-ва непрерывных ф-ций: в
в отрезке:
1. Если ф-ция y=f(x) непрерывна на [a, b] и f(a)*f(b)< 0, т. е. знаки f(a) и f(b) противоположны, то на (a, b) найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.
2. Если ф-ция y=f(x) непрерывна на [a, b], то она ограничена на этом промежутке.
3. Если ф-ция y=f(x) непрерывна на [a, b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).
в точке:
1. если ф-ция f(x) и g(x) непрерывна в х0, то их сумма, произведение, частное (при j(х0)¹ 0) явл-ся ф-циями, непрерывными в х0
|
|
|
2. если ф-ция y=f(x) непрерывна в х0, и f(x0)> 0, то существует окрестность х0, в которой f(x)> 0
3. если y=f(U) непрерывна в U0, а U=j(x) непрерывна в U0=j(x0), то сложная ф-ция y=f[j(x)] непрерывна в х0.
39. Задачи, приводящие к понятию производной. Определение производной и ее геометрический смысл.
1. ncp. =DS/Dt, n=lim(DS/Dt), где Dt®0
2. pcp. =Dm/Dl, pT=lim(Dm/Dl), где Dl®0
Dy=f(x+Dx)-f(x), y=f(x)
lim(Dy/Dx)=lim((f(x+Dx)-f(x))/Dx)
Dx®0 Dx®0
Смысл производной - это скорость изменения ф-ции при изменении аргумента.
y=f(x+Dx)-f(x), y=f(x). производной в точке а называется предел отношения приращения ф-ции к приращению аргумента:
lim(Dy/Dx)=lim((f(x+Dx)-f(x))/Dx)=dy/dx
Dx®0 Dx®0
Вычисление производной: lim(Dy/Dx)=y` Dx®0
1) если y=x, Dy=Dx, y`=x=lim(Dy/Dx)=1.
2) если y=x2, Dy=(x+Dx)2-x2=x2+2xDx+Dx2-x2=Dx(2x-Dx),
(x2)`=lim((Dx(2x+Dx))/Dx)=lim(2x+Dx)=2x
x®0 Dx®0
Геометрический смысл производной.
KN=Dy, MK=Dx
DMNK/tg2=Dy/Dx
вычислим предел левой и правой части:
limtga=lim(Dy/Dx) Dx®0
tga0=y`
a®a0
При Dx®0 секущая MN®занять положение касательной в точке M(tga0=y`, a®a0)
Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x0.
40. Основные правила дифференцирования.
Теорема: Если f(x) и g(x) дифферен. в точке х, то: 
Теорема о произв. сложной функции:
Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Теорема о произв. обратной функции.
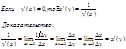
Таблица производных:
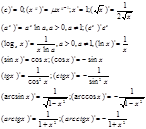
41. Дифференцирование сложных ф-ций:
Производная сложной ф-ции = произведению производной ф-ции по промежуточному аргументу и производной самого промежуточного аргумента по независимой переменной.
y`=f(x)*U`, или yx`=yU`*Ux`, или dy/dx=dy/dU=dU/dx
Например:
42. Дифференцирование обратной ф-ции.
y=f(x), то x=j(y) - обратная ф-ция.
Для дифференцируемой ф-ции с производной, не = 0, производная обратной ф-ции = обратной величине производной данной ф-ции, т. е. xy`=1/yx`.
|
|
|
Dy/Dx=1/(Dy/Dx) - возьмем предел от левой и правой части, учитывая, что предел частного = частному пределов:
lim(Dy/Dx)=1/(lim(Dy/Dx), т. е. yx`=1/xy или f`(x)=1/j`(x)
Например:
|
|
|
