 |
43. Производные степенных и тригонометрических функций.
|
|
|
|
43. Производные степенных и тригонометрических функций.
Основные формулы: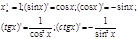 
44. Производные обратных тригонометрических функций.
Основные формулы: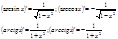 
Для сложных функций:
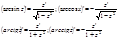
45. Производные показательных и логарифмических функций.
Основные формулы:
Если z=z(x) – дифференцируемая функция от x, то формулы имеют вид:
46. Логарифмическое дифференцирование. Вывод производной степенной ф-ции.
y=ax - показательная ф-ция, y=xn - степенная, y=xx - показательно-степенная.
y=[f(x)]j(x) - показательно-степенная ф-ция.
lny=xlnx - найдем производную от левой и правой части, считая у ф-цией х.
(1/y)*y`=(lny)
(x*lnx)`=x`lnx+x*(lnx)`=lnx+1
y`=y*(lnx+1)=xx(lnx+1)
Операция, которая заключается в последовательном применении к ф-ции y=f(x) сначала логарифмирование, а затем дифференцирование.
Степенная ф-ция:
1. y=xn, nlnx, y`/y=n/x=n*(x)-1
y`=y*n*(x-1)=n*xn*x-1=n*xn-1
2. y=eU, где U=sinx
U`=cosx, y`=(eU)`=eU*U`=esinx*cosx.
47. Производная высших порядков ф-ции 1й переменной.
y=f(x)
y``=(y`)`=lim((f`(x+Dx)-f`(x))/Dx)
x®0
y```=(y``)`= lim((f``(x+Dx)-f``(x))/Dx)
f(n)(x)=[f(n-1)(x)]`
48. Производные 1, 2-го порядка неявных ф-ций.
Неявной называется такая ф-ция у аргумента х, если она задана уравнением F(x, y)=0, не разрешенным относительно независимой переменной.
y=f(x), y=x2-1 - явные
F(x, y)=0, a2=x2+y2 - неявные ф-ции.
1)a2=x2+y2 - найдем производную, продифференцируем, считая у - сложной ф-цией х.
y`=2x+2y=0, т. к. а- постоянная
y*y`=-x, y`=-x/y
2) x3-3xy+y3=0
3x3-3(xy)`+3y2*y`=0 //: 3
x2-(x`y+y`x)+y2*y`=0
y`y2-xy`=y-x2
y`=(y-x2)/(y2-x)
49. Дифференциал ф-ции и его геометрический смысл. Св-ва дифференциала.
limy=A, y=A+a
limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx
Dx®0
Dy=y`Dx+e, где e-б. м. в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.
dy=y`Dx
Дифференциалом ф-ции наз. величина, пропорциональная б. м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б. м. в. более высокого порядка малости, чем Dх.
|
|
|
Если y=x, то dy=dx=x`Dx=Dx, dx=Dx
Если y¹ x, то dy=y`dx, y`=dy, dx
Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x0, f(x0)) при изменении x0 на величину Dx
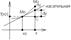
Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)
2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV
3. d(c)=c`dx=0*dx=0
4. d(U/V)`=(V`dU-U`dV)/V2.
50. Теорема Ролля.
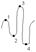Если функция f(x) непрерывна на заданном промеж/ [a, b] деффер. на интервале (a, b) f(a)=f(b) то существует т. с из интерв. (a, b), такая, что f’(c)=0.
51. Теорема Лагранжа.
Если функция f(x) непрерывна на [a, b] и дефференцирована на (a, b), то сущест.
т. с(a, b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство: применим т. Коши, взяв только g(x)=x, тогда g’(x)=1¹ 0.
52. Теорема Коши.
Если f(x), g(x) удовл. трем условиям:
1). f(x), g(x) непрерыв. на промеж [a, b]
2). f(x), g(x) деффер. на интервале (a, b)
3). g’(x)¹ 0 на интер. (a, b), то сущ. т. с
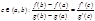
g(b)¹ g(a) (неравны по теореме Ролля).
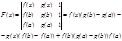
1). F(x) – непрерывна на [a, b]
2). F(x) – деффиренцирована на (a, b)
3). F(a)=0; F(b)=0
по теореме Ролля сущ. сÎ (a, b); F’(с)=0
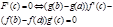
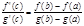
53. Необходимые и достаточные признаки монотонности ф-ции:
Если x2> x1, f(x2)> f(x1), то ф-ция монотонно возрастает
Если x2> x1, f(x2)< f(x1), то ф-ция монотонно убывает
Монотонность - постоянство
Необходимые признаки: 1)если ф-ция f(x) всюду в интервале возрастает, то ее производная в этом интервале неотрицательна (f`(x)> =0)
2)если ф-ция f(x) всюду в интервале убывает, то ее производная в этом интервале неположительная (f`(x)< =0)
3)если ф-ция f(x) всюду в интервале постоянна, то ее производная в этом интервале =0 (f`(x)=0)
Достаточные признаки монотонности: 1)если f`(x) в интервале положительна, то ф-ция f(x) возрастает в этом интервале.
2)если f`(x)< 0, то ф-ция f(x) возрастает в этом интервале.
|
|
|
3)если f`(x)=0, то ф-ция f(x)=const на интервале.
x1< a< x2, x2-x1> 0, x2> x1
1. если f`(a)> 0, то f(x2)> f(x1)
2. если f`(a)< 0, то f(x2)< f(x1)
3. если f`(a)=0, то f(x2)=f(x1)
|
|
|
