 |
Проективная прямая. Проективная плоскость
|
|
|
|
Проективная прямая
Попробуем найти ответ на вопрос, поставленный в конце предыдущей главы: какие свойства фигур остаются неизменными при центральном проецировании? Для этого поступим следующим образом. Рассмотрим центральную проекцию плоскости α на плоскость α '. Если эти две плоскости параллельны, то такое проецирование будет простым преобразованием подобия (гомотетией), поэтому будем в дальнейшем рассматривать случай, когда плоскости α и α ' пересекаются.
Для того, чтобы понять, какие свойства фигур останутся при этом неизменными, начнем с простейших фигур – точек и прямых. На первый взгляд все обстоит совсем просто: точки переходят в точки, прямые – в прямые, если прямая m проходит через точку А, то ее проекция m' проходит через проекцию точки А, точку А'. Однако даже здесь начинают возникать проблемы.
Рассмотрим центральную проекцию прямой m на прямую m'. Прямая ОА пересекает m' в точке А', и, значит, точка А' является проекцией точки А. Но вот прямая ОВ параллельна прямой m'. Значит, точке В не соответствует никакая точка прямой m'. Зато, если взять на прямой m' точку С' такую, что ОС' параллельна m, то получается, что на прямой m не найдется точки, проекцией которой служит точка С'.
Будем двигать точку А вдоль прямой m по направлению к точке В. Чем ближе точка А к точке В, тем дальше уходит по прямой m' ее проекция А'. В тот момент, когда точки А и В совпадают точка А' «уходит в бесконечность», а затем появляется с другой стороны на прямой m'.
Если двигать точку А все дальше и дальше по прямой m, то ее проекция на прямой m' будет приближаться к точке С'. Но достигнуть этого предельного положения точка А' сможет лишь тогда, когда точка А на прямой m «уйдет в бесконечность».
|
|
|
Чтобы придать формальный смысл этим рассуждениям, добавим к каждой прямой еще одну «бесконечно удаленную точку». Теперь можно сказать, что проекцией точки В является бесконечно удаленная точка прямой m', а бесконечно удаленная точка прямой m проецируется в точку С' на прямой m'.
Заметим, что проективная прямая, полученная из обычной евклидовой прямой добавлением бесконечно удаленной точки, стала замкнутой. Если двигаться по ней вправо, то пройдя через бесконечно удаленную точку мы вернемся слева. Таким образом, взяв на проективной прямой две точки А и В, мы не можем рассмотреть отрезок АВ. Эти точки просто разобьют прямую на две равноправные части, подобно тому, как две точки разбивают окружность на две дуги.
Можно, конечно, сказать, что одна из этих частей в отличие от другой содержит бесконечно удаленную точку, но здесь необходимо осознать, что на проективной прямой бесконечно удаленная точка не занимает никакого особого положения. Нельзя сказать, что «вот эта точка прямой – обыкновенная, а вот эта – особенная, бесконечно удаленная».
Действительно, при центральном проецировании «бесконечно удаленная» точка одной прямой переходит в «обычную» точку другой прямой, так что свойство точки «быть бесконечно удаленной» не сохраняется при центральной проекции или, как говорят, не является проективным свойством.
Здесь уместна следующая аналогия. Когда мы строим изображение многогранника, некоторые ребра мы считаем «видимыми» и изображаем жирными линиями, а другие – «невидимыми» и проводим пунктиром. Однако нельзя сказать, что многогранник обладает ребрами двух разных типов. Так и каждая точка проективной прямой может стать бесконечно удаленной только по отношению к конкретному чертежу.
Проективная плоскость
Подобно тому, как проективная прямая получается из евклидовой прямой добавлением одной «бесконечно удаленной» точки, так и проективная плоскость может быть получена добавлением к евклидовой плоскости одной «бесконечно удаленной» прямой. На этой прямой лежат все бесконечно удаленные точки всех прямых плоскости. При этом будем считать, что прямые, которые на евклидовой плоскости являются параллельными, на проективной плоскости пересекаются в бесконечно удаленной точке.
|
|
|
Таким образом, в проективной геометрии отсутствует понятие параллельности. Любые две прямые пересекаются. Нет смысла различать при этом в какой точке они пересекаются, «обычной» или «бесконечно удаленной». Все точки проективной плоскости логически равноправны.
При центральном проецировании одной плоскости на другую «бесконечно удаленная» прямая одной плоскости перейдет в «обычную» прямую другой плоскости, а прямые которые выглядели «параллельными» станут пересекающимися.
Таким образом, на проективной плоскости нет параллельных прямых, нельзя обычным образом измерить расстояние между точками, угол между прямыми. В самом деле: чему равен угол между прямой m и бесконечно удаленной прямой? Более того, нас интересуют только те свойства фигур, которые сохраняются при центральной проекции. Ясно, что расстояния между точками и углы между прямыми не сохраняются, то есть не являются проективными свойствами.
Нельзя также сказать, что из трех точек одной проективной прямой одна лежит между двумя другими, как нельзя, например, сказать это о трех точках окружности.
Значит, на проективной плоскости нельзя определить такие фигуры как отрезок или даже треугольник. Можно, конечно, провести три прямые, которые пересекутся в трех разных точках. Такую фигуру называют трехсторонником или трехвершинником. Но если попытаться выделить на чертеже «внутреннюю область», ограниченную этими прямыми, то при центральном проецировании эта область может перестать быть «треугольником» в привычном смысле слова, как это видно на рисунке 8.
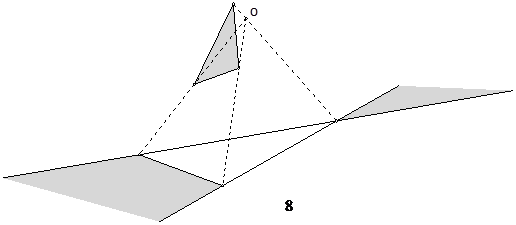
Различие между «треугольниками» на рисунках 9 и 10 состоит в том, что один из них пересекает «бесконечно удаленную прямую». С проективной точки зрения никакой разницы между ними нет. Значит три прямые, не проходящие через одну точку, делят проективную плоскость на четыре части. Каждую из этих частей можно было бы назвать, скажем, «проективным треугольником», но в дальнейшем это нигде не пригодится.
|
|
|
 |
На первый взгляд, проективных свойств у фигур не так уж и много. Например, если три прямые проходят через одну точку, то это свойство (конкурентность прямых) сохранится в любой центральной проекции. Также, очевидно будет сохраняться расположение точек на одной прямой (коллинеарность точек). В дальнейшем увидим, что другие проективные свойства фигур сводятся к этим двум основным – коллинеарности и конкурентности. Кажется, что проективная геометрия гораздо беднее обычной евклидовой геометрии. Однако это совсем не так, в чем мы вскоре убедимся.
Определив проективную плоскость, путем пополнения евклидовой плоскости бесконечно удаленной прямой, будем теперь действовать следующим образом: рассуждения и доказательства будем проводить на евклидовой плоскости, используя расстояния, углы и все известные теоремы евклидовой геометрии. Если же удастся обнаружить какое-либо проективное свойство, не зависящее от углов, расстояний, отношений отрезков и т. п. будем переходить на проективную плоскость.
|
|
|
