 |
Теорема Паппа. Прямые МА', МВ, МС', MD' образуют четверку с тем же сложным отношением, что и точки А', В, С', D'
|
|
|
|
Теорема Паппа
Воспользуемся свойствами сложного отношения точек и прямых для доказательства еще одной теоремы.
Рассмотрим центральную проекцию прямой АВ на прямую А'В, с центром в точке S. Точка В остается на месте, точки А, D и С переходят в точки А', D' и С'. При этом сложные отношения (АВ, СD) и (А'В, С'D') равны между собой. Проведем через точку В произвольную прямую, пересекающую прямые SA и SC в точках М и N.
 |
Прямые МА', МВ, МС', MD' образуют четверку с тем же сложным отношением, что и точки А', В, С', D'. (МА' МВ, МС' MD') = (А'В, С'D') = (АВ, СD). Пересечем прямые этого пучка прямой АС' и рассмотрим перспективное отображение пучка с вершиной М на пучок с вершиной N и осью перспективы АС'.
Прямая МА' перейдет в прямую NA, прямая МС' – в NС, прямая МВ – сама в себя. Образом прямой MD' будет прямая пучка с вершиной N, проходящая через точку К пересечения оси перспективы АС' и прямой MD'. Сложное отношение прямых сохраняется. (NA NB, NC NK) = (МА' МВ, МС' MD').
Прямые NA, NB, NC, NK пересекают прямую АВ в точках А, В, С, D1, и сложное отношение точек пересечения равно сложному отношению прямых пучка.
(АВ, СD1) = (NA NB, NC NK) = (МА' МВ, МС' MD') = (А'В, С'D') = (АВ, СD)
Это значит, что точка D совпадает с точкой D1. Убирая с чертежа некоторые точки и прямые и вводя новые обозначения, получаем теорему Паппа.
Теорема Паппа
Пусть X, Y, Z и X', Y', Z'– коллинеарные тройки точек. Прямые XY' и X'Y пересекаются в точке А, прямые YZ' и Y'Z – в точке В, прямые ZX' и Z'X – в точке С. Тогда точки А, В, С коллинеарны.
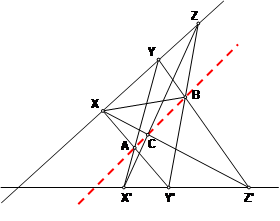
Перед нами замечательный пример проективной теоремы. В условии даны две коллинеарные тройки точек, и в заключении получаем еще одну коллинеарную тройку. Исходные тройки точек можно располагать на прямых в любом порядке, получая разнообразные, непохожие друг на друга чертежи, но точки А, В, С обязательно будут лежать на одной прямой.
|
|
|
 | |||
 | |||
Всего в рассмотренную конфигурацию входят девять точек и девять прямых. На каждой прямой лежат по три точки, через каждую точку проходят три прямые. Попытка воспользоваться принципом двойственности и обменять местами точки и прямые приведет лишь к тому, что мы получим эквивалентную формулировку той же самой теоремы.
Пусть x, y, z и x', y', z' – две тройки конкурентных прямых. Соединим точки пересечения прямых x, y' и x', y прямой а, точки пересечения y, z' и y', z – прямой b, точки пересечения z, x' и z', x – прямой c. Тогда прямые a, b, c конкурентны.
Построив чертеж к двойственной теореме, увидим ту же самую конструкцию из девяти прямых и девяти точек.
Интересно, что в теореме Паппа речь идет о «дважды дезарговых» трехвершинниках. Рассмотрим два трехвершинника, образованных прямыми XY', YZ', ZX' и X'Y, Y'Z, Z'X. Назовем их KLM и PQR. Точки пересечения сторон KL и QR, LM и PQ, MK и PR – это точки X, Y, Z, лежащие на одной прямой. Точно так же точки пересечения сторон KL и PR, LM и QR, MK и PQ – это точки X', Y', Z', лежащие на одной прямой. Теорема Паппа утверждает, что эти трехвершинники являются даже «трижды дезарговыми», то есть точки пересечения сторон KL и PQ, LM и PR, MK и RQ также лежат на одной прямой.
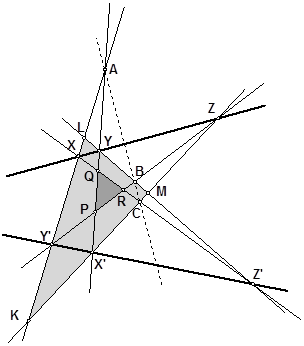
Кажется очень естественной попытка доказать теорему Паппа, используя теорему Дезарга. Однако, Гильберт в своей знаменитой книге «Основания геометрии» показал, что попытки получить доказательство теоремы Паппа, только применяя к различным парам трехвершинников на чертеже теорему Дезарга, не могут привести к успеху. Теорема Паппа оказывается в каком-то смысле «глубже» теоремы Дезарга. Обратный ход оказывается вполне возможным. Теорему Дезарга можно доказать, используя теорему Паппа. Разумеется, речь идет о «проективных» доказательствах без использования пропорций, отношений или, тем более, расстояний между точками..
|
|
|
Теорема Паппа знаменита прежде всего тем, что это первая проективная теорема. Папп сформулировал и доказал ее примерно за полторы тысячи лет до возникновения проективной геометрии. При этом он не рассматривал ни проекций, ни сложных отношений.
Попробуйте сами доказать теорему Паппа, используя только теоремы школьного курса евклидовой геометрии. Нет сомнений, что на этом пути вас ожидают определенные трудности. Для этого, видимо, придется многократно применять к различным треугольникам теорему Менелая или теорему Чевы. Возможно есть и другие пути доказательства. Кто знает?... Не зря же Папп был назван последним великим геометром античности.
|
|
|


