 |
Произвольное отображение коники на себя
|
|
|
|
Лемма
Композиция двух центральных отображений с центрами S и P является проективным отображением с осью SP.
Применим к точке А центральное отображение с центром S, а к ее образу центральное отображение с центром Р. Получим точку А'. Таким же образом из точки В получим точку В'. Точка пересечения прямых АВ' и А'В должна лежать на оси отображения. По теореме Паскаля все такие точки лежат на прямой SP. Значит она и будет осью отображения.
Теорема
Композиция трех центральных отображений, центры которых лежат на одной прямой, является центральным отображением с центром на той же прямой.
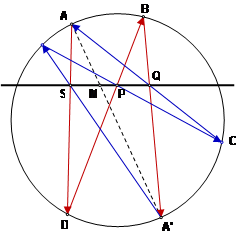Рассмотрим композицию трех центральных отображений с центрами S, P, Q. Применяя последовательно три отображения, построим образ точки А – точку А'.
Построим теперь образ точки А' при этой же композиции отображений. По теореме Паскаля мы вернемся обратно в точку А.
Значит, при композиции трех центральных отображений с центрами S, P, Q точки А и А' меняются местами. Следовательно это – центральное отображение. Назовем его центр М.
Последовательное применение всех четырех центральных отображений возвращает любую точку на ее исходное место или, как говорят, является тождественным отображением.
Значит, применяя к любой точке композицию отображений с центрами S и P, или же композицию отображений с центрами М и Q, (в обратном порядке! ) будем получать один и тот же результат. Следовательно, осью этой композиции служит как прямая SP, так и прямая МQ. Это и значит, что точка М лежит на прямой, проходящей через точки S, P, Q.
Построим теперь все четыре центральные отображения для двух различных точек А и В. Получаем следующий результат:
|
|
|
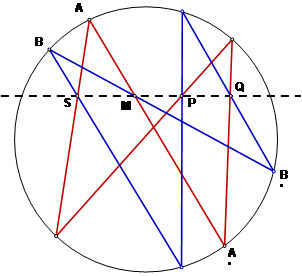
Если в конику вписаны два четырехсторонника и точки пересечения трех соответственных сторон лежат на одной прямой, то и точка пересечения двух оставшихся сторон также лежит на этой прямой.
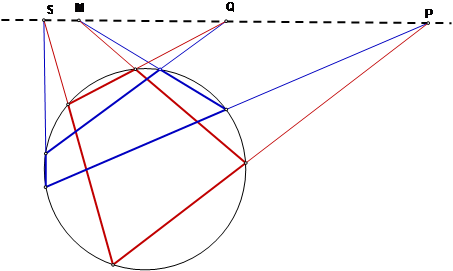
Интересно было бы найти «школьное» доказательство этой теоремы для двух четырехугольников, вписанных в окружность.
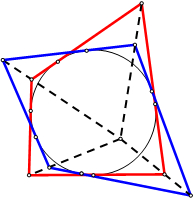
Можно, конечно же, сформулировать и двойственную теорему. Для этого построим полярное отображение. Вместо вписанных четырехсторонников появятся описанные четырехсторонники, а теорема станет звучать так:
Если вокруг коники описаны два четырехсторонника и прямые, соединяющие три соответствующие вершины, проходят через одну точку, то и прямая, соединяющая оставшиеся две вершины, также проходит через эту точку.
Рассматривая композицию трех произвольных центральных отображений коники на себя, получаем решение следующей задачи
Дана окружность (коника) и три произвольные точки, ей не принадлежащие. Построить треугольник (трехсторонник), вершины которого лежат на окружности (конике), а стороны проходят через данные точки.
Действительно, задача сводится к тому, чтобы найти неподвижную точку отображения, которое является композицией трех центральных отображений. Для этого достаточно построить образы трех произвольных точек А, В и С при этом отображении, и по трем точкам и их образам А', В' и С' построить ось отображения. Точки пересечения этой оси с коникой и будут неподвижными точками. Каждая из неподвижных точек является вершиной одного из искомых трехсторонников.
К сожалению, чертеж к задаче получается весьма запутанным и перегруженным вспомогательными линиями, так что нет смысла приводить его здесь. Гораздо полезнее построить его самостоятельно.
Произвольное отображение коники на себя
В самом начале мы рассматривали проективные отображения прямой на прямую. Но две прямые представляют собой вырожденный случай конического сечения. В таком случае, отображение одной прямой на другую есть частный случай отображения коники на себя, а центральная проекция одной прямой на другую соответствует центральному отображению коники.
|
|
|
Рассмотрим отображение одной прямой на другую, не являющееся центральной проекцией. Как известно, прямые, соединяющие соответственные точки, образуют линейную оболочку некоторой коники. Оказывается, это утверждение оказывается верным и для невырожденной коники.
|
|
|
